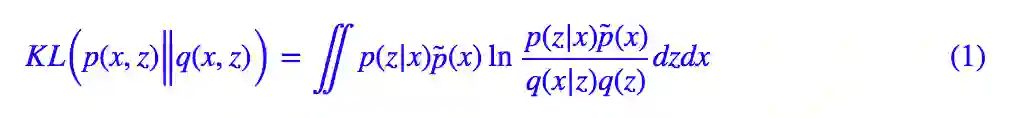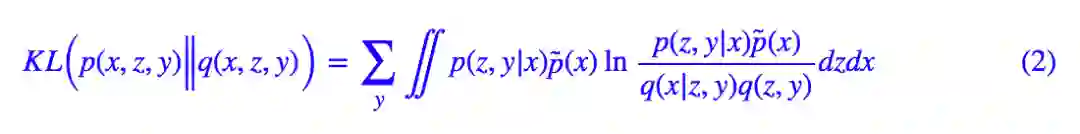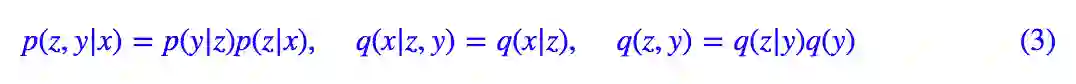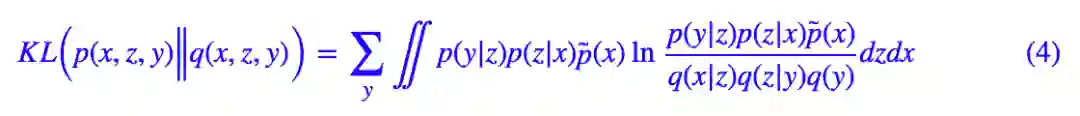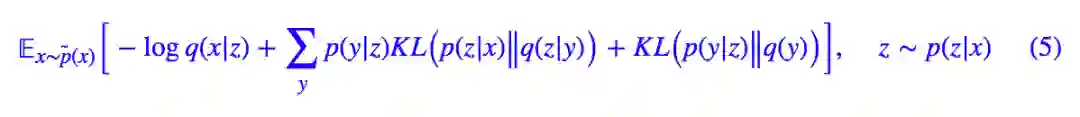变分自编码器VAE：一步到位的聚类方案

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

由于 VAE 中既有编码器又有解码器（生成器），同时隐变量分布又被近似编码为标准正态分布，因此 VAE 既是一个生成模型，又是一个特征提取器。

在图像领域中，由于 VAE 生成的图片偏模糊，因此大家通常更关心 VAE 作为图像特征提取器的作用。提取特征都是为了下一步的任务准备的，而下一步的任务可能有很多，比如分类、聚类等。本文来关心“聚类”这个任务。

一般来说，用 AE 或者 VAE 做聚类都是分步来进行的，即先训练一个普通的 VAE，然后得到原始数据的隐变量，接着对隐变量做一个 K-Means 或 GMM 之类的。但是这样的思路的整体感显然不够，而且聚类方法的选择也让我们纠结。

本文介绍基于 VAE 的一个“一步到位”聚类思路，它同时允许我们完成无监督地完成聚类和条件生成。

理论

一般框架

回顾 VAE 的 loss（如果没印象请参考再谈变分自编码器VAE：从贝叶斯观点出发）：

通常来说，我们会假设 q(z) 是标准正态分布，p(z|x),q(x|z) 是条件正态分布，然后代入计算，就得到了普通的 VAE 的 loss。

然而，也没有谁规定隐变量一定是连续变量吧？这里我们就将隐变量定为 (z,y)，其中 z 是一个连续变量，代表编码向量；y 是离散的变量，代表类别。直接把 (1) 中的 z 替换为 (z,y)，就得到：

这就是用来做聚类的 VAE 的 loss 了。

分步假设

啥？就完事了？呃，是的，如果只考虑一般化的框架，(2) 确实就完事了。 

不过落实到实践中，(2) 可以有很多不同的实践方案，这里介绍比较简单的一种。首先我们要明确，在 (2 )中，我们只知道 p̃(x)（通过一批数据给出的经验分布），其他都是没有明确下来的。于是为了求解 (2)，我们需要设定一些形式。一种选取方案为：

代入 (2) 得到：

其实 (4) 式还是相当直观的，它分布描述了编码和生成过程：

1. 从原始数据中采样到 x，然后通过 p(z|x) 可以得到编码特征 z，然后通过分类器 p(y|z) 对编码特征进行分类，从而得到类别；

2. 从分布 q(y) 中选取一个类别 y，然后从分布 q(z|y) 中选取一个随机隐变量 z，再通过生成器 q(x|z) 解码为原始样本。

具体模型

(4) 式其实已经很具体了，我们只需要沿用以往 VAE 的做法：p(z|x) 一般假设为均值为 μ(x) 方差为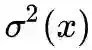的正态分布，q(x|z) 一般假设为均值为 G(z) 方差为常数的正态分布（等价于用 MSE 作为 loss），q(z|y) 可以假设为均值为 μy 方差为 1 的正态分布，至于剩下的 q(y),p(y|z)，q(y) 可以假设为均匀分布（它就是个常数），也就是希望每个类大致均衡，而 p(y|z) 是对隐变量的分类器，随便用个 softmax 的网络就可以拟合了。 

最后，可以形象地将 (4) 改写为：

其中 z∼p(z|x) 是重参数操作，而方括号中的三项 loss，各有各的含义：

1. −log q(x|z) 希望重构误差越小越好，也就是 z 尽量保留完整的信息；

2.希望 z 能尽量对齐某个类别的“专属”的正态分布，就是这一步起到聚类的作用；

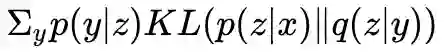
3. KL(p(y|z)‖q(y)) 希望每个类的分布尽量均衡，不会发生两个几乎重合的情况（坍缩为一个类）。当然，有时候可能不需要这个先验要求，那就可以去掉这一项。

实验

实验代码自然是 Keras 完成的了，在 MNIST 和 Fashion-MNIST 上做了实验，表现都还可以。实验环境：Keras 2.2 + TensorFlow 1.8 + Python 2.7。

代码实现

代码位于：

https://github.com/bojone/vae/blob/master/vae_keras_cluster.py 

其实注释应该比较清楚了，而且相比普通的 VAE 改动不大。可能稍微有难度的是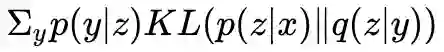这个怎么实现。因为 y 是离散的，所以事实上这就是一个矩阵乘法（相乘然后对某个公共变量求和，就是矩阵乘法的一般形式），用 K.batch_dot 实现。 

其他的话，读者应该先弄清楚普通的 VAE 实现过程，然后再看本文的内容和代码，不然估计是一脸懵的。

MNIST

这里是 MNIST 的实验结果图示，包括类内样本图示和按类采样图示。最后还简单估算了一下，以每一类对应的数目最多的那个真实标签为类标签的话，最终的 test 准确率大约有 84.5%，对比这篇文章 Unsupervised Deep Embedding for Clustering Analysis [1] 的结果（最高也是 84% 左右），感觉应该很不错了。 

聚类图示

按类采样

Fashion-MNIST

这里是 Fashion-MNIST [2] 的实验结果图示，包括类内样本图示和按类采样图示，最终的 test 准确率大约有 60.6%。 

聚类图示

按类采样

总结

文章简单地实现了一下基于 VAE 的聚类算法，算法的特点就是一步到位，结合“编码”、“聚类”和“生成”三个任务同时完成，思想是对 VAE 的 loss 的一般化。

感觉还有一定的提升空间，比如式 (4) 只是式 (2) 的一个例子，还可以考虑更加一般的情况。代码中的 encoder 和 decoder 也都没有经过仔细调优，仅仅是验证想法所用。

参考文献

[1]. Unsupervised Deep Embedding for Clustering Analysis Junyuan Xie, Ross Girshick, and Ali Farhadi in International Conference on Machine Learning (ICML), 2016.

[2]. https://github.com/zalandoresearch/fashion-mnist

点击以下标题查看更多相关文章： 

• 变分自编码器VAE：原来是这么一回事 | 附开源代码

• 再谈变分自编码器VAE：从贝叶斯观点出发

• 变分自编码器VAE：这样做为什么能成？

• 漫谈概率 PCA 和变分自编码器

• 全新视角：用变分推断统一理解生成模型

• PaperWeekly 第二十七期 | VAE for NLP
  

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？ 答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。

▽ 点击 | 阅读原文 | 查看作者博客