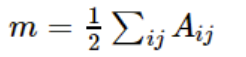图机器学习经典算法 louvain 完全解读
本文原创作者知乎主页链接为
https://www.zhihu.com/people/he-he-he-he-77-19-21
louvain 算是目前市面上提到的和使用过的最常用的社区发现算法之一了,除此之外就是 infomap,这两种。
模块度是评估一个社区网络划分好坏的度量方法,它的物理含义是社区内节点的连边数与随机情况下的边数之差,它的取值范围是 [−1/2,1),其定义如下:
这个公式的含义一定要理解清楚才能体会到 louvain 背后的真谛。
为了更好的理解这里举一个具体的例子:
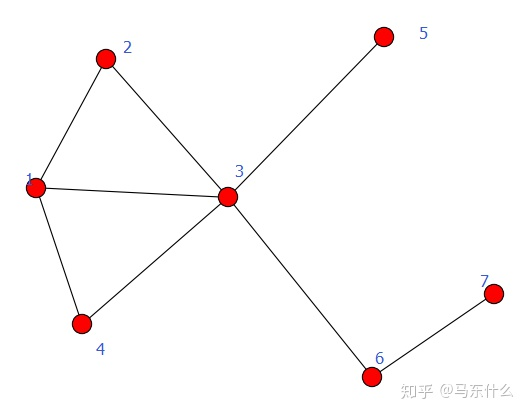
实际上的情况是这样的,假设我们有一个 graph 如上,这个社区 graph 中有 7 个 nodes,为了方便起见我们假设所有 edges 的权重均为1(带权的计算方式和下面是完全一样的),这个时候我们先计算整个 graph 的边的权重
:
(这里需要注意, 的计算是重复的,比如我们以 node 为当前节点的时候,计算了一次 edges 的权重之和,例如 和 , 和 , 和 . 当我们以node 为当前节点进行计算的时候,我们的计算是 和 , 和 , 和 。可以发现 和 这两个 nodes 进行 edges 的求和的时候, 和 实际上是重复计算了,因此实际上计算总的 edges 的权重之和的时候,每条edge 的权重都被重复计算了两次,所以 m 的公式前面有个 1/2.)
比如假设当前 , ,则 (节点和自身之间不存在 edge,权重为 0), (无 edge 连接,权重也是 0),则对于 来说其计算结果为 3,同理,计算结果是2,则对所有的 nodes 都进行如上的两轮循环的遍历之后,得到的 的计算结果是:
node 1:3 、 node2:2 、 node3:5、node4:2、node5:1、node6:2、node7:1
则求和之后的结果为:16
但是实际上我们一共就 8 条 edges,每条 edges 的权重为 1,总权重之和为 8,这里计算结果为 16 就是因为 edges 之间重复计算的问题,因此m的结果才要在前面加 1/2 才表示真实的权重;
然后回到我们定义随机情况的问题上,我们的 节点对外的连接的权重之和为 ,则节点 连接到任意一个节点的概率本来直观上的感觉应该是 的,但实际的情况是这样的,我们的 graph 上任意两个节点相互连接的组合有:
node1-node2
node1-node3
node1-node4
……
node2-node1
node2-node3
……
node6-node3
node6-node7
node7-node6
一共是 即 16 种可能的情况,注意,像 node1-node2 和 node2-node1 要当作两种不同的情况;因为从 node2 到 node1 和从 node1 到 node2 的权重率不一定是相同的,例如存在双向,且双向的权重不同的情况;因为很多文章里的例子都是简单的双向等权的情况,所以这个地方容易搞错;
这样我们就明白了为啥使用 来表示节点 和任意一个节点连接的概率;

那么现在,对于除了 节点之外的某一个节点 ,其权重为 ,则我们可以得到随机情况下,节点i和节点j的权重值的期望值: .
这样我们对于原始公式的物理意义以及背后的含义就解读完毕了,接下来开始化简:
模块度的原始公式比较复杂,只要记住简化之后的公式就可以:

表示对所有的社区的后面式子的结果进行累加。需要注意,初始第一轮迭代的时候,我们是把所有的 nodes 都当作一个独立的社区,并且这个社区的权重为0;那么接下来就是对每一个社区进行这样的计算:
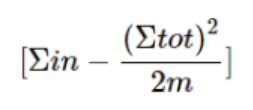
其中 表示当前社区里所有边的权重之和,比如 node A 和 node B 相连并且在一个社区,这个社区只有 A 和 B 两个 nodes,则这个社区的权重就是 A->B 和 B->A 的连接的 edge 的权重之和;
表示社区 C 与其他社区连边的权重和。这样的话,实际上上述公式的意义比较好理解,显然如果我们希望我们的模块度 越大越好,就是希望我们的社区内的边的权重之和尽量越大越好,而我们的社区与外界的连接的权重越小越好。
然后是模块度增益的公式:
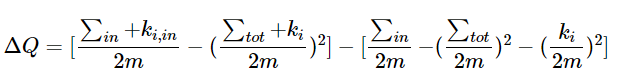
这个地方很多文章没有写清楚,实际上 的计算含义是非常明确的:
社区 C 加入节点 i 之后的模块度-(社区 C 原始的模块度 + 节点 i 原始的模块度)
(graph的模块度是全部的社区的模块度之和)
只不过这个地方公式被省略了……
对于单个节点来说,其模块度的公式也是:
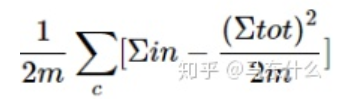
但是对于单个节点来说,其社区内部权重没有意义(因为就一个点哪来的内部权重的概念,因此这里对于单个点来说, 的值是0,所以就只剩下后面这一项了:
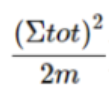
根据tot的定义,tot表示所有与社区连接的外部的edges的权重之和,那么对于单个node来说,其与外部社区连接的edges的权重之和其实就是,所有与节点 i 相连的边的权重之和,也就是这里的 ,那么公式一套进去就得到结果了。)因此我们的模块度增益的最终公式是:
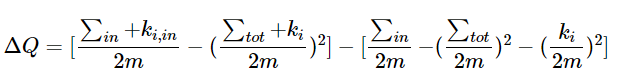
化简可以得到:
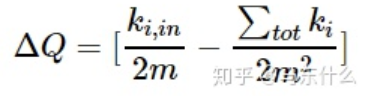
进一步化简可以得到:
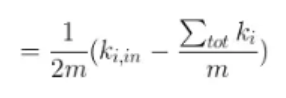
上式可以理解为:括号内第一项 表示实际节点i与要移入社区之间的实际的,真实存在的连接的边的权重之和,
第二项∑tot/m 为 除了社区内部之外,其它节点与该社区连接的概率,
∑tot/m * ki则为基于随机的情况下节点i 在其权重为k的情况下与该社区连接的边的权重的期望. 第一项若比第二项大则说明节点i与该社区连接程度超过随机连接的程度(即存在一定关系超越了随便的关系), 则加入到该社区, 反之保持不变。
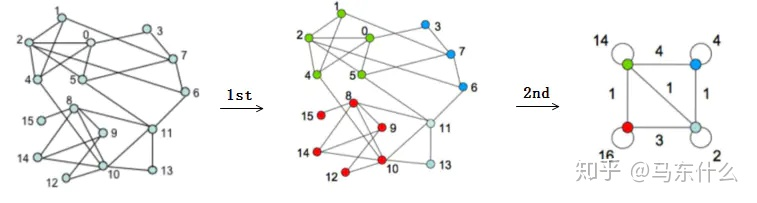
需要注意的是,当我们第一轮划分出社区之后,每个社区实际上是合并为一个大的nodes的,这个nodes是一个self-loop的nodes,其权重就是原始的社区里所有nodes的连接权重之和;
这里为了更好的理解,我们还是举个例子:
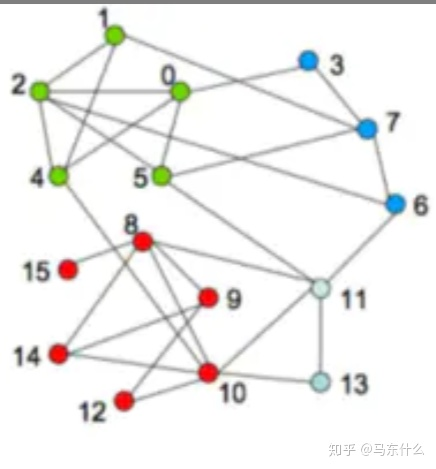
我们以上图节点1和节点2之间的计算为例,初始,每个节点都当作一个社区,则我们尝试对节点1和节点2进行合并,以节点2为社区,节点1为算法尝试合并的node。根据公式:
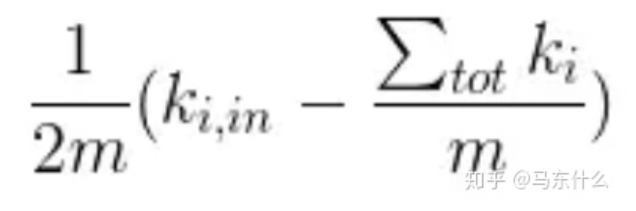
;
求和符号(tot)/m=5/m(节点2和节点1、节点4、节点5、节点6以及节点0存在连接)
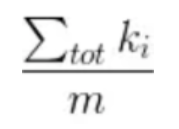
=5/m*3(节点1和节点2、4、7连接),这里m的值是很大的.我懒得数有多少条了,这里假设100条吧,则可以计算出来增益的结果是正的;
同样的过程,以node2为社区,再去计算0、4、5、6这四个节点的模块度增益,最后取最大的模块度增益的节点进行合并,假设是节点2和节点4进行了合并,则我们将node2和node4合并为一个自环的node2_4,其权重为2、4节点之间连接的权重为1。依次类推;
总结:
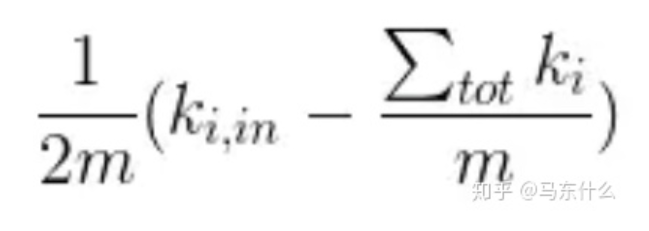
我们只要记住这个公式就可以了,就是加入新的节点后,这个节点与当前社区的连接的实际权重,与随机情况下,这个节点和当前社区的连接的权重的期望进行相减,如果结果为正,说明这个节点和社区之间存在着一点也不“随便”的关系,并且结果越大,越不“随便”;
关于 Louvain 分群的几点思考
① 如何评价分群质量 Louvain算法采用的是无向图,无向图模块度的理论值范围时[-0.5,1]。从 Louvain 分群过程看,算法迭代的目标是增加每个模块模块度,所以可从分完群后图整体的模块度评价分群质量,模块度越大分群质量越高。我们图分群后1级群模块度在0.3~0.7之间,2级群在0.4~0.8之间。
② Louvain 分群的局限从实际效果看,在图大了后分离小群会合并为大群。从算法原理也可以解释这个局限。Louvain 分群在计算模块度增量时是利用群内边连接数目减去随机图中节点与该群连接边数。当图非常大了后,假设节点的权重本身很小比如1,那么随机情况下,节点连到任1个群的概率都非常小,即模块度增量第二项非常小,那么只要两个群之间有一条边相连,群都会合并。解决这个局限是图萃取,我们采用的方法是先给边设置权重,然后通过边权重过滤连接比较弱的边,然后分群。同时边权重细分可以提升度数较高的节点分群质量。我们应用 Louvain 分群过程如下图5所示。
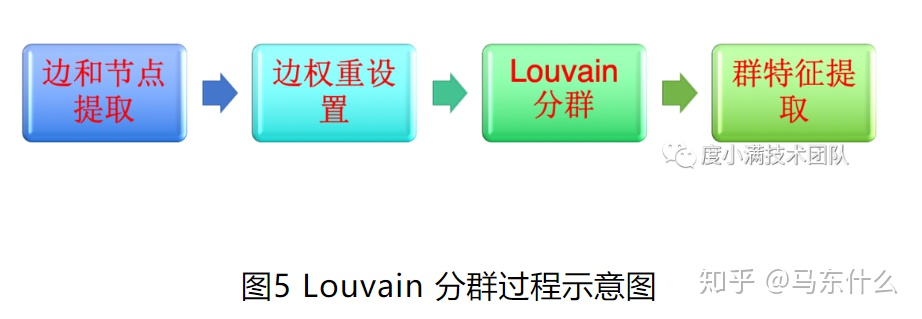
实际上louvain本身就存在权重的概念,只不过很多时候我们都当作简单的无权图来对待,实际上在实施louvain算法之前,我们可以先做一些去噪的工作,比如去除权重很小的edges;
参考自:
Louvain算法的介绍与利用Graphx的实现过程 (https://www.jianshu.com/p/460022a413c8)
模块度与Louvain社区发现算法(https://www.cnblogs.com/fengfenggirl/p/louvain.html)