如何重构图神经网络？98页LoG2022《图重连:从理论到应用》教程，附代码

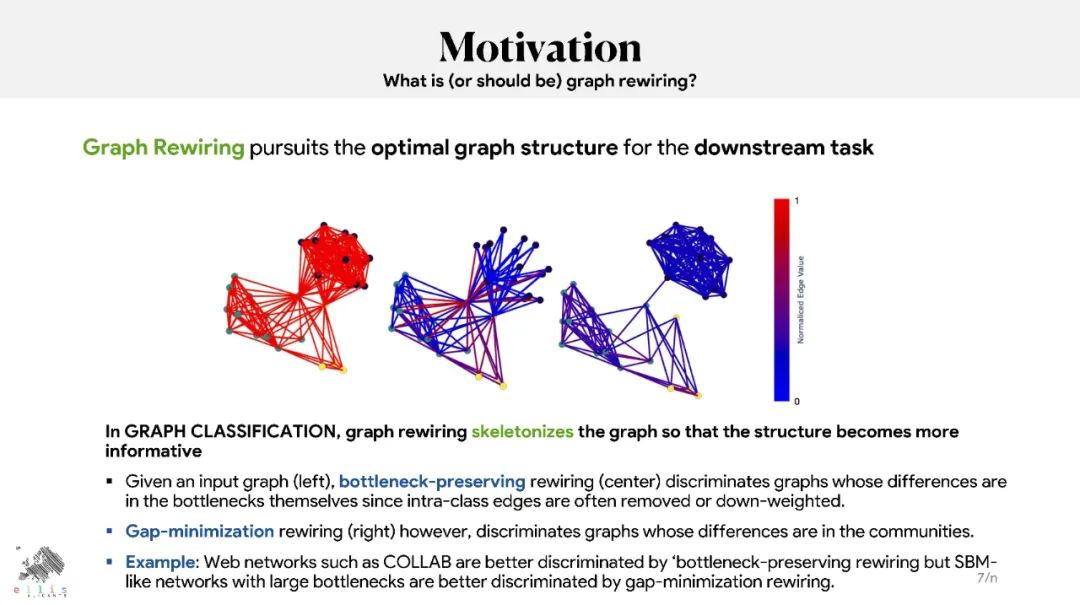
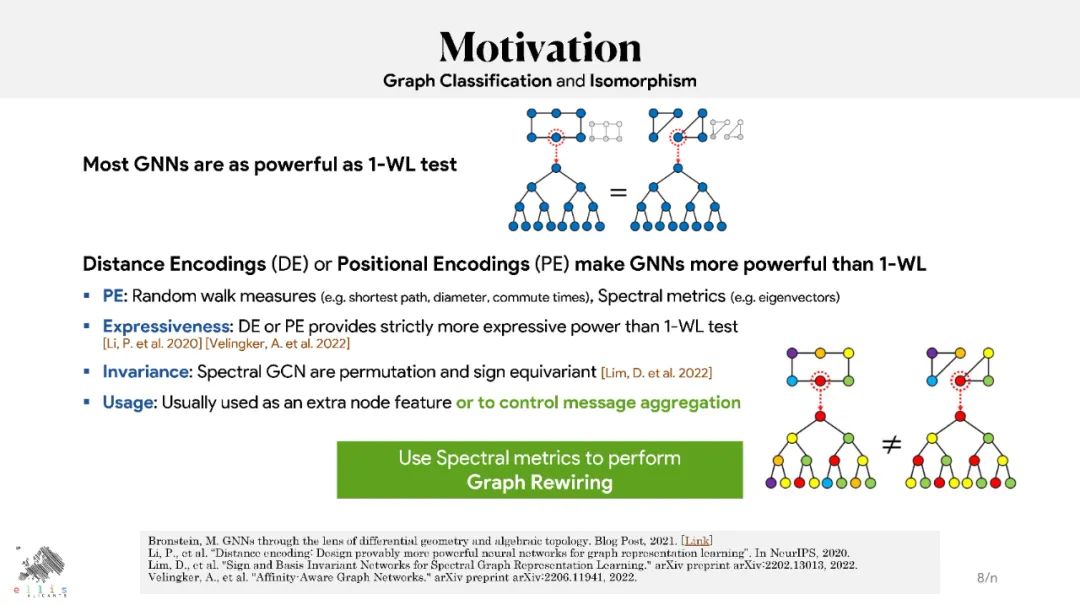
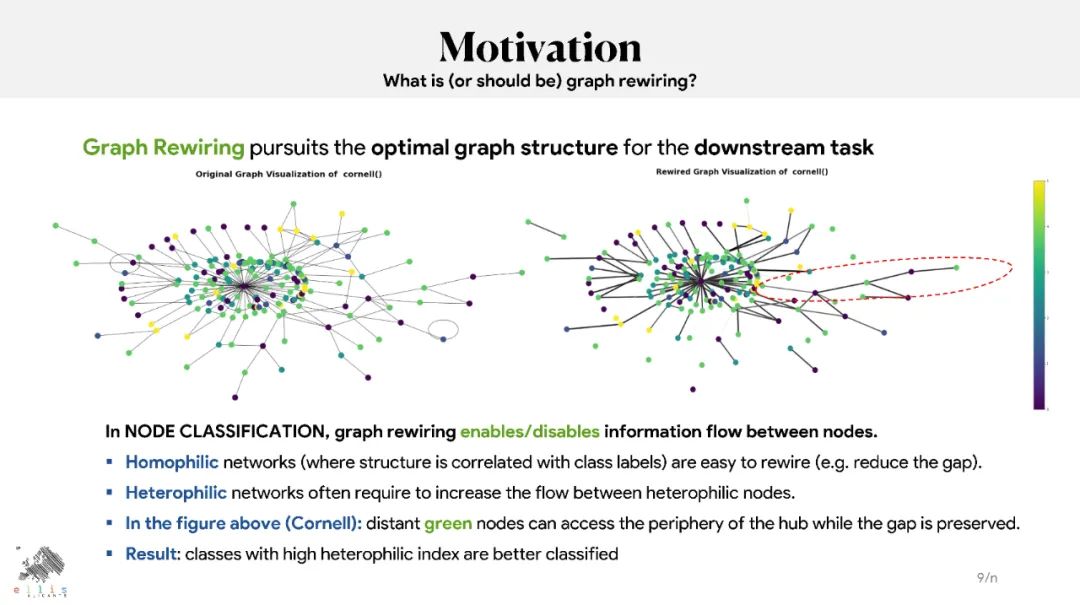
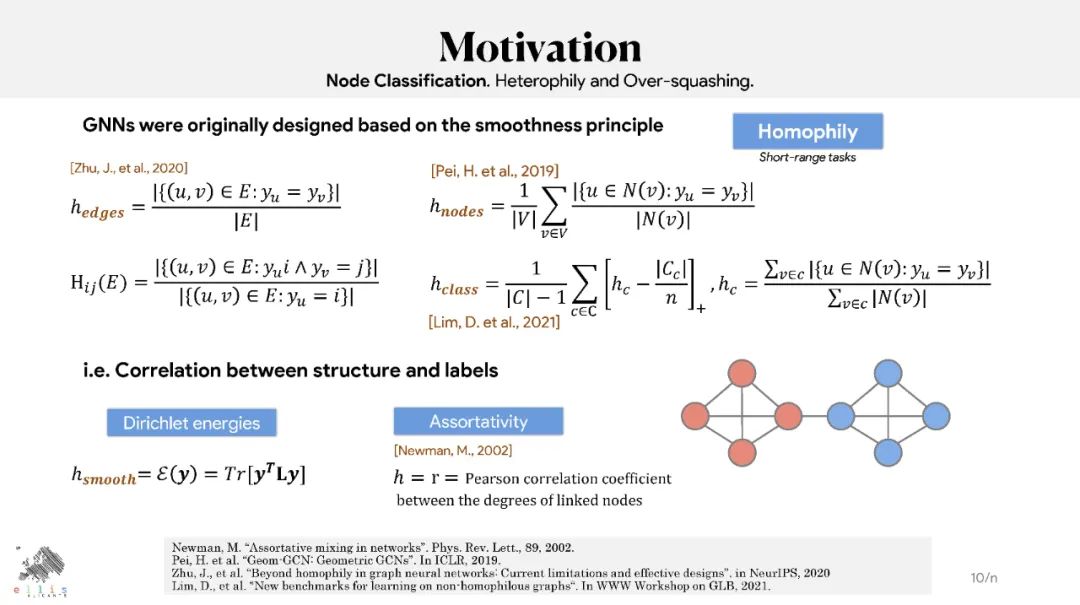
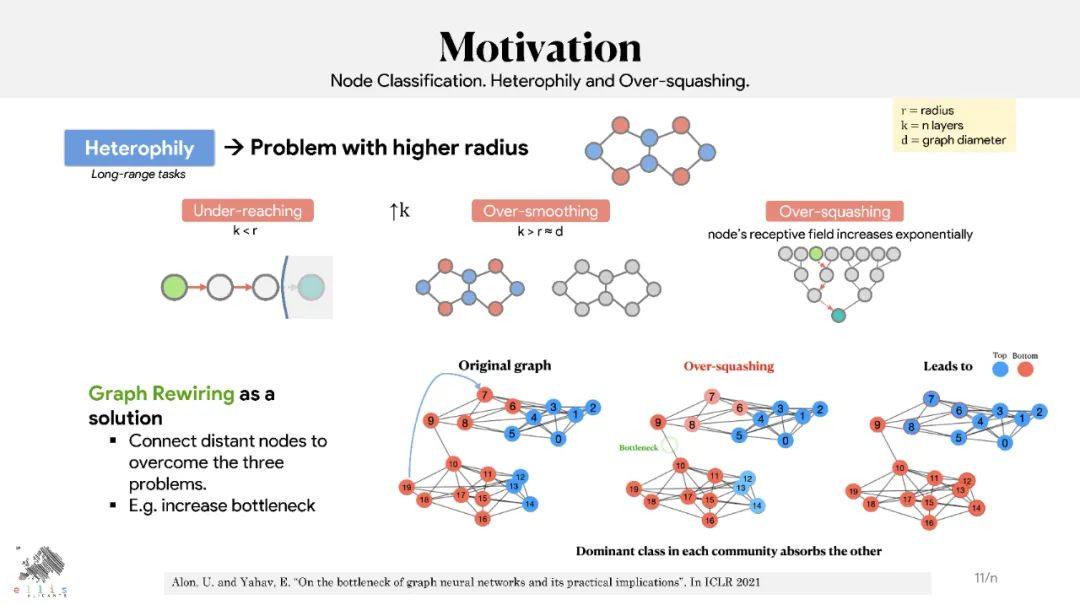
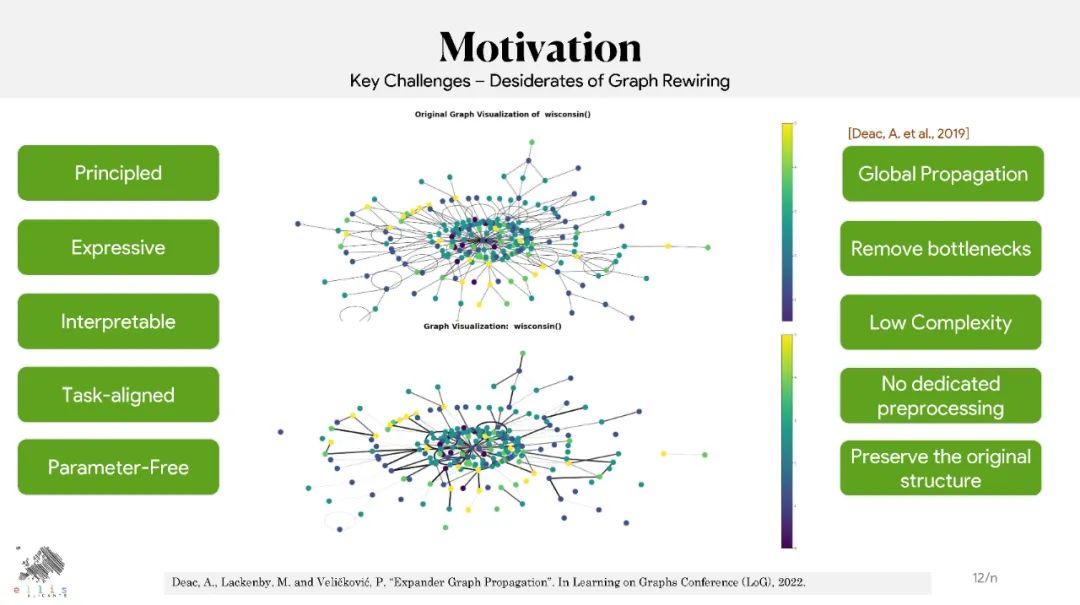
图神经网络(GNN)已被证明在处理与图相关的任务方面取得了有竞争力的结果，如节点和图分类、链接预测以及各种领域中的节点和图聚类。尽管结果很有希望，但据报道GNN存在过度平滑、过度挤压和不足。文献中提出了图重连和图池化作为解决这些限制的解决方案。图重连包括修改(编辑和/或重新加权)图的边，以便针对特定任务(如图/节点分类或链接预测)优化信息流。许多图重连方法依赖于边采样策略:首先，根据相关函数为边分配新的权重，然后根据新的权重对它们进行重新采样，以保留最相关的边(即那些具有较大权重的边)。计算边缘相关性的方式有很多种，包括随机计算、基于相似度计算或基于边缘曲率计算。本教程提供了文献中提出的基于扩散、曲率或谱概念的图重连的最相关技术的概述。它将解释它们的关系，并将介绍最相关的最先进的技术及其在不同领域的应用。本教程将从理论、经验和伦理的角度概述这一领域的开放性问题。

本教程的主要目标是教授图形重连的基础知识及其当前的挑战。我们将激发对数学上合理的图重连方法的需求，作为解决GNN的主要限制的解决方案:欠延伸、过度平滑和过度挤压。我们将解释文献中提出的实现图重连的两种主要方法:

• 直推式方法计算每个图的新卷积矩阵作为预处理步骤，以提高手头任务的性能。例如参数化扩散或基于曲率的方法。

• 归纳方法从子图/图的训练中学习新的卷积矩阵，然后预测未见图中的卷积矩阵。理想情况下，这个过程是完全可微的和无参数的。我们将深入研究这些方法的实现。

此外，我们将讨论图重连在解决人工智能带来的社会和道德挑战方面的潜力，特别是作为实现算法公平的工具。