【ETHZ博士论文】神经最优传输用于动力学系统：生物医学中的方法与应用, 239页pdf

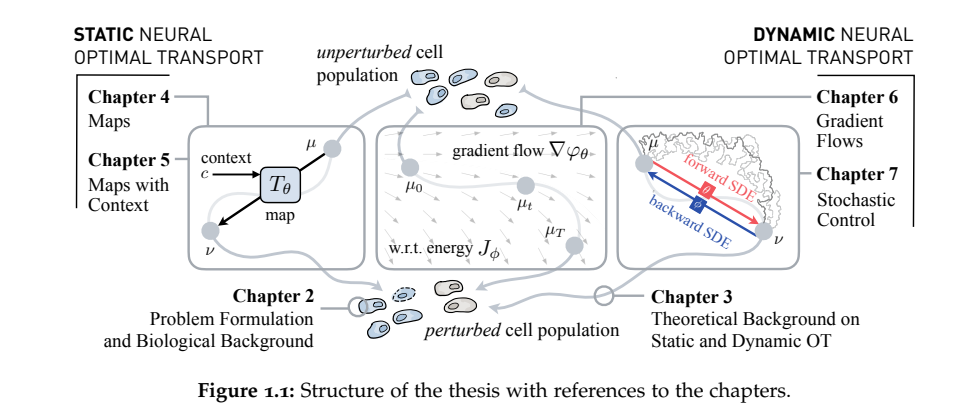
对动力系统的建模是许多科学学科的核心主题，因为它允许我们预测未来的状态，了解复杂的时间交互，并使得决策更加明智。特别是生物系统，它们由动力过程控制，其固有的复杂且不断变化的交互和行为模式。单细胞生物学已经彻底改变了生物医学研究，因为它允许我们在前所未有的规模上监测这些系统。与此同时，它也带给我们巨大的挑战：尽管单细胞高通量方法经常产生数百万的数据点，但它们是破坏性的测验，因此不能对同一个细胞进行两次观察或随时间进行分析。由于该领域许多最为迫切的问题涉及对异质细胞群体对各种刺激（如治疗药物或发展信号）的动态反应进行建模，因此迫切需要提供能够规避该限制并重新对齐这些未配对测量的计算方法。最优传输(OT)已经成为填补这一空白的一个重要机会，因为它允许我们重建分布是如何演化的，只给定不对齐的数据点的不同快照。然而，经典的OT方法不能泛化到未见过的样本。

但当预测即将到来的患者样本的治疗反应或超出测量范围的细胞动态时，这是至关重要的。通过利用OT的理论结构，这篇论文探索和开发了用于阐明生物群体复杂动态的神经静态和动态最优传输方案。它封装了一系列算法框架，对群体动态的理解和预测都有所贡献：首先，我们推导出能够学习未受扰和受扰细胞之间未配对分布之间映射的静态神经最优传输方案。这些模型擅长预测对不同扰动的单细胞反应，如癌症药物筛选，并将治疗结果的推断泛化到未观察到的细胞类型和患者。这对个性化医疗有重要意义，因为它允许在大规模的临床研究中预测新患者的治疗反应。

其次，我们探索了利用OT与部分微分方程和通过Jordan-Kinderlehrer-Otto方案的梯度流，以及通过扩散薛定谔桥的随机微分方程和最优控制的联系的动态神经最优传输公式。这些方法随后作为从边际观察中重建随机和连续时间动态的强大工具，允许我们剖析细粒度和时间分辨的细胞机制。

这篇论文将众多看似无关的概念连接成一个统一的框架，所呈现的方法为细胞动态的建模提供了计算和数学基础。这为了解细胞异质性、可塑性和反应景观提供了新的途径。这种对静态和动态OT的神经参数化允许对样本之外的推断，为发现新的生物学现象、从单细胞患者样本中推断个性化治疗方法和推动再生医学的边界提供了令人兴奋的机会。