从数学推导开始，7万字一定带你学会支持向量机（附118PDF下载）

转载机器之心报道机器之心编辑部

本书从零推导 SVM，涵盖从 SVM 的思想、到形式化、再简化、最后实现的完整过程。

SVM（Support Vector Machine，支持向量机）是一个非常经典且高效的分类模型。在机器学习领域，有两大类方法既理论优美又能在实践中取得很好的效果，其中一类是 SVM 及其衍生的核方法和统计学习理论；另一类是 AdaBoost 及其衍生的 Boosting 方法，例如在 Kaggle 竞赛中十分流行的 XGBoost 和 LightGBM 即属于 Boosting 方法。目前十分热门的深度学习方法虽然在实践中能取得十分突出的效果，但是理论支持不够完善。

在深度学习复兴之前，SVM 是最常被使用的模型之一。即使现在深度学习如火如荼，在一些领域 SVM 仍有其用武之地；此外，理解 SVM 对理解机器学习领域的关键概念和重要思想很有帮助；最后，因为 SVM 的影响力，其常常作为面试问题用于考察面试者的基本功。因此，SVM 是机器学习及相关领域初学者必须掌握的算法之一。

电子书概览

但是，SVM 涉及许多数学推导，有些还比较复杂，并且需要比较强的凸优化基础知识，这使得一些初学者虽花大量时间和精力研读，但仍一头雾水，最终望而却步，从入门到放弃。本书《手把手带你学懂 SVM》旨在从零推导 SVM，涵盖从 SVM 的思想、到形式化、再简化、最后实现的完整过程。

电子书下载地址：https://pan.baidu.com/link/zhihu/7QhkzYuRhtikYhNkkFdf1qRHewTqJVRwZBVW==
知乎链接：https://zhuanlan.zhihu.com/p/480302399

例如，SVM 涉及许多概念，比如间隔（又分为硬间隔和软间隔）、支持向量、基本型、对偶型、高斯核函数等，本书一方面会从数学角度详细定义和解释每个概念，另一方面会通过通俗的例子直观说明这些概念的含义，以帮助读者理解。

举个例子，假设读者要学习《高等数学》这门课，用机器学习的语言来进行描述，读者平时在上课的过程就是训练读者成为 “《高等数学》学习模型” 的过程，平时进行的模拟考试或做的练习就是训练样本，最终的期末考试就是训练样本之外的测试样本，用来测试读者对《高等数学》知识的掌握情况，即检验读者对运用《高等数学》知识解题的泛化能力。

如果读者在模拟考试或练习（即训练样本）上只能达到 60 分或只比 60 分多几分，即十分接近及格和不及格的分类边界，虽然在模拟考试或练习中及格了（即训练样本预测正确），但是如果期末考试（即测试样本）和模拟考试或练习（即训练样本）相比变了些题型（进行了一些局部扰动），那么读者很有可能在期末考试上不及格（即测试样本预测错误）。

不同的同学有不同的学习策略（即不同的学习模型有不同的归纳偏好），SVM 的归纳偏好类似于 “学霸” 的学习策略，“学霸” 不满足于模型考试或练习只及格就可以，而是不仅是要在模型考试或练习中及格（即训练样本预测正确）、而且进一步要使得模型考试或练习的成绩尽量比 60 分高，比如达到 70 分或 80 分以上（即训练样本远离划分超平面），那么期末考试及格（即测试样本预测正确）的概率会很大。

从上面的例子可以了解到，训练样本是平时做的模拟考试或练习，测试样本是期末考试。基本型就像是闭卷考试，在期末考试时（即在预测阶段），你平时做的模拟考试或练习都不能带（即不依赖训练集 D），只能靠你聪明的头脑进行答题（即只能使用训练得到的参数 (w⋆,b⋆) 进行预测）；而对偶型就像是开卷考试，在期末考试时（即在预测阶段），你可以带平时做过的模拟考试或练习（即依赖训练集 D），答题时不仅可以靠你聪明的头脑，还可以查阅平时做过的模拟考试或练习（即同时使用训练得到的参数和训练集 D 进行预测）。

基本型属于参数模型、而对偶型属于非参数模型。可以看出，参数模型的特点在于预测过程简单、预测耗时短（即闭卷考试时会就是会、不会就是不会，花再多时间也没啥用）；而非参数模型的特点在于模型表示能力通常更强（读者应该有体会，通常开卷考试的成绩更高），但预测过程比较复杂、预测耗时长，预测耗时通常和训练集大小 m 成正比（即答题时需要将带的模拟考试或练习翻找一遍）。

更进一步，训练样本是平时做的模拟考试或练习，硬间隔要求你对平时做的所有的模拟考试或练习分数都要比 60 分高很多，而软间隔允许你有几次失误的机会，即允许有少量模拟考试或练习分数接近或低于 60 分。软间隔和硬间隔相比会放松一些要求，这样更加现实，有时候模拟考试或练习中会存在偏题怪题（即噪声样本），如果一味追求要所有的模拟考试或练习都做的很好（即硬间隔），那么会花大量的时间纠结偏题怪题（即拟合噪声样本），不见得期末考试成绩会好（即容易出现过拟合）。

训练样本是平时做的模型考试或练习，测试样本是期末考试，支持向量是错题集，基本型是闭卷考试，对偶型是开卷考试。那么软间隔高斯核 SVM 的对偶型告诉你，在开卷考试时不需要带所有做过的模拟考试或练习（即不需要全部训练集 D），只需要带错题集（即只需要支持向量），在期末考试答题时采用的策略是（即预测策略是），拿到一道题（即对于一个待预测的样本），将该题和错题集中收录的题一一比对一遍（即基于核函数对支持向量进行相似度计算），参考错题集中的解法（即参考支持向量的标记），相似度高的题解法就多参考参考、相似度低的题解法就少参考参考（即基于核函数得出的相似度进行加权投票），不过参考不是照抄，还需要你聪明的大脑进行加工和整合（即基于进行加权投票）得到最终解法（即最终预测结果）。其实回顾你以前参加开卷考试的经历，使用的基本上就是这个答题策略，所以软间隔高斯核 SVM 的对偶型的表示能力十分强大。

下表对 SVM 中涉及的一些概念用学习《高等数学》课程的例子进行类比，类比不见得严谨，但是有助于理解概念。我们学习机器学习还有一个意义是促进人类的学习，SVM 中的很多思想和策略对人类学习很有启发价值。

本书有以下特点：

数学推导详细。对于一些数学性比较强的资料，读者有时会卡在其中的一两个关键步骤，无法理解其中的推导过程，导致无法学习后续的内容。本书会详细推导所有涉及的公式，数学基础比较好的读者可以快速浏览推导过程作为回忆和巩固；而对于数学基础有些薄弱的读者，详细的推导过程将使读者不会 “掉队”；
补充背景知识。SVM 是凸优化领域的经典算法，需要读者对凸优化的背景知识有一定的了解。但是大部分读者可能并不是数学或优化背景出身，为了学习 SVM 先要掌握内容宏大的凸优化知识会是比较重的负担。为了减轻读者的负担并能使尽可能多的读者从中收益，本书不要求读者有凸优化背景知识，读者只需要有基础的微积分和线性代数背景即可。文本对 SVM 中涉及的背景知识会进行补充，力图使本书内容是自足的，即争取做到 “学懂 SVM 只看本书就够了”；
概念图文结合。SVM 的另一个难点是涉及许多概念，有些还比较抽象。因此，本书配备了许多插图，用于辅助读者学习。读者如果能自动地做到将各个术语和概念对应到图中，那基本就可以达到对 SVM 融会贯通的程度；
包含面试问题。本书内容涵盖了常见的对 SVM 的面试考察问题，因此也可以作为快速回顾和复习 SVM 的参考资料；
穿插趣味示例。本书如果通篇都是对 SVM 的数学推导不免有些抽象和乏味，因此会多次用人类学习《高等数学》知识这一例子类比 SVM 中的重要概念和思想。类比不见得严谨，但对理解 SVM 具有帮助意义。

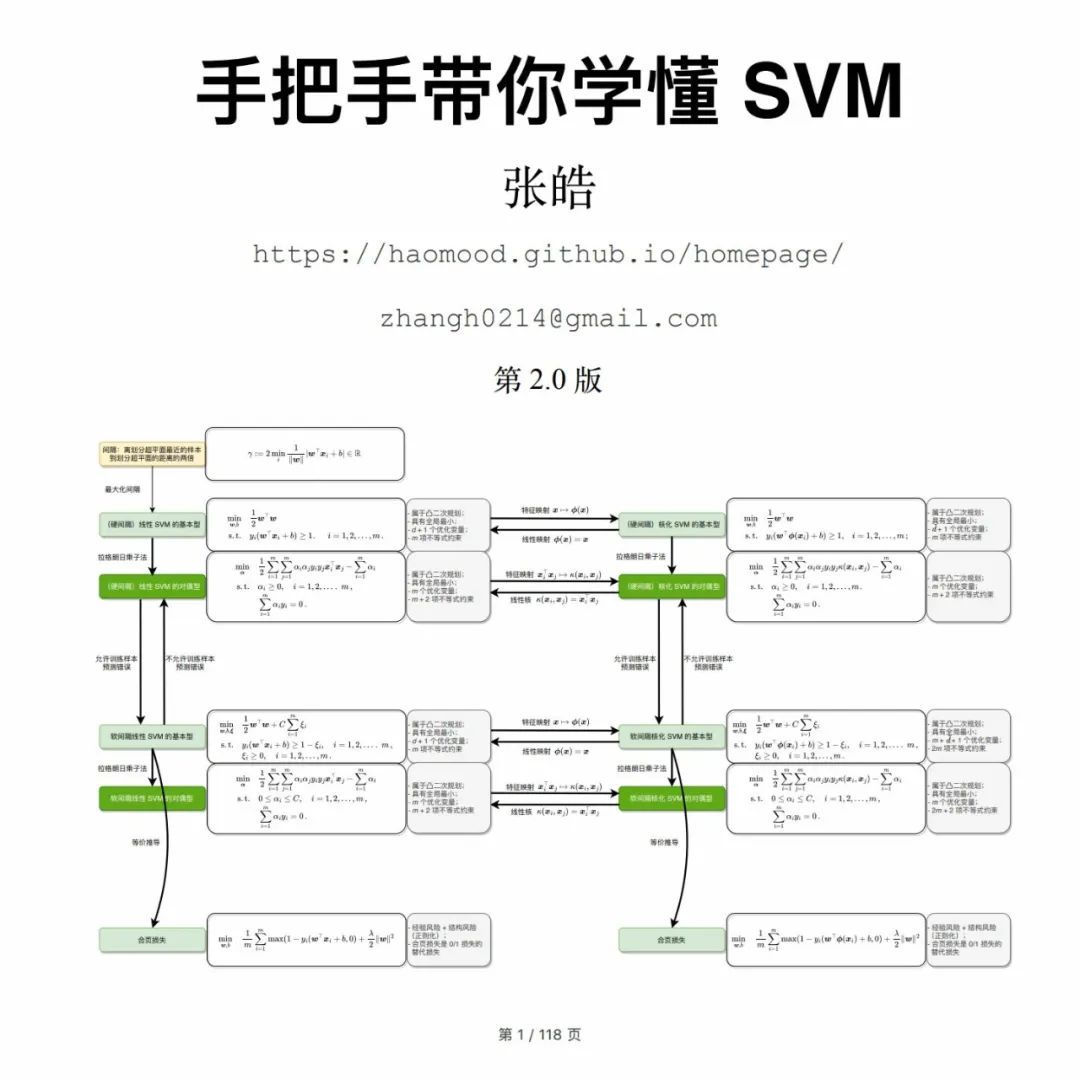
SVM 中涉及的关键内容可以用下图进行概括，本书将从最基础的部分进行，逐步深入，每一步都尽量提供详细的推导过程，使读者能跟上本书的节奏。

作者自认才疏学浅，仅略懂皮毛，更兼时间和精力有限，文中错谬之处在所难免，敬请读者批评指正，本书勘误请发送邮件至：zhangh0214@gmail.com。 作者介绍**

张皓，毕业于南京大学计算机系周志华教授领导的机器学习与数据挖掘研究所（LAMDA），导师为吴建鑫教授，研究方向为深度学习和计算机视觉，曾获国家奖学金、江苏省三好学生等荣誉。发表论文累计被引超过 240 次，著有《深度学习视频理解》一书、合译《模式识别》一书，曾获 2016 年 CVPR 视频表象性格分析竞赛世界冠军。现任腾讯在线视频研究员，专注于腾讯视频等场景下的相关视频理解任务。曾任腾讯优图实验室研究员，为微信等场景提供相关视频理解能力。个人主页：https://haomood.github.io/homepage/，知乎号 “张皓”，担任多个自媒体作者或专栏作者。

书籍目录