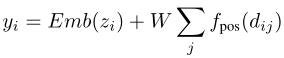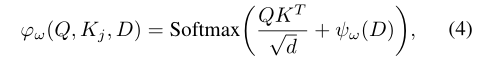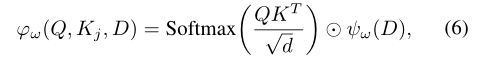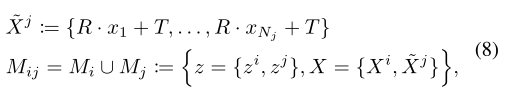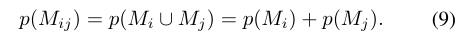作者 | 李政毅审核 | 黄 锋
今天给大家介绍的是特拉维夫大学发表在IJCAI-2022上的一篇文章:"Geometric Transformer for End-to-End Molecule Properties Prediction"。由于Transformer能够表征元素之间复杂的相互作用,已经成为许多应用中的首选方法。然而,将Transformer架构扩展到非序列数据如分子数据,并使其在小数据集上进行训练仍然是一个挑战。在这项工作中,作者为分子属性预测引入了一个基于Transformer的架构,通过对分子几何形状的初始编码以及学习到的门控自我注意机制来修改经典的位置编码器,能够捕获分子的几何形状。同时,作者进一步提出了一个分子数据的增强方案,能够避免过度参数化引起的过拟合。所提出的框架优于最先进的方法,同时完全基于纯机器学习,即该方法不包含量子化学领域的知识,也不使用除成对原子距离之外的扩展几何输入。
1 研究背景
化合物的性质通常可以使用密度泛函理论或从头计算量子化学等方法来估计。但是这些方法的计算成本很高,因此其适用性有限。近年来,许多方法已经开始利用机器学习来降低有效预测分子性质所需的计算复杂性。在这方面,许多贡献集中在创建原子或分子水平的手工表示,作为各种机器学习方法的输入。薛定谔方程表明,给定分子的基态性质仅是原子间距离和核电荷的函数。基于这一发现,最近的几种方法以端到端的方式预测分子性质,其中输入由原子的类型和空间位置定义。这些方法通常包含量子化学知识,并依赖于广泛的超参数调整。 作者的模型不使用扩展的领域知识,仅基于简单的距离相关性假设,即原子元素之间的距离越大,相互作用越小。与其他工作相反,该框架没有假定任何扩展的输入,例如量子力学性质,复杂的几何信息,如弯曲或扭转角度等。作者设计的Transformer被赋予了一个适应的位置编码器,并在模型的不同级别上学习了原子间的几何嵌入,允许增加表征能力,同时可以保持分子对刚性变换和排列的不变性。
2 模型介绍
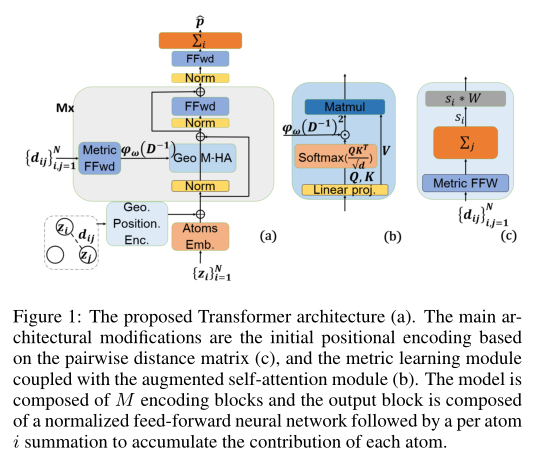
模型的整体架构
Geometric Positional Encoding
分子预测必须满足基本对称性和物理定律的不变性,例如对刚性空间变换(旋转和平移)和相同类型原子的置换不变性。因此,模型中的位置输入被变换为原子间的欧氏距离,以保持刚性变换的不变性,而置换不变性是通过相同类型原子的相同的初始原子特征来实现。 由于原子的初始嵌入完全基于原子的类型,无法区分相同的的原子,且省略了分子的几何结构。原始Transformer的位置编码模块旨在将序列元素的接近程度传入到初始嵌入。在分子预测任务中,由于输入被定义为集合而不是序列,因此需要调整位置编码器以提供几何感知的初始嵌入。在这里,作者使用原子间距离矩阵来为每个原子嵌入传入位置信息,如下所示:
和分别表示原子i的初始嵌入以及原子i和其他原子之间的欧氏距离,位置编码可以提原子的初始几何感知嵌入
Geometric Self-Attention
自注意机制使得能够准确地学习分子几何结构信息以及分子复杂的几何相互作用。作者提出将原子的成对距离信息加入到自注意力层的计算中,自注意力层将会被扩展为如下的形式:
从上图可以看出,如果两个原子的欧式距离超过给定的截止距离,那么ψω将趋近于0,同时二者通过注意力层计算的分数应该是趋近于0。在这之前,已经提出了几种方法来扩展自注意机制,如下公式(4)和(5)所示:
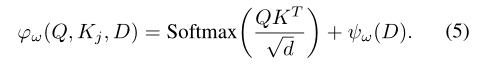
通过这种方式,原子间的距离将会对注意力层计算的原子间的分数产生直接的影响。
Learning the Graph Geometry
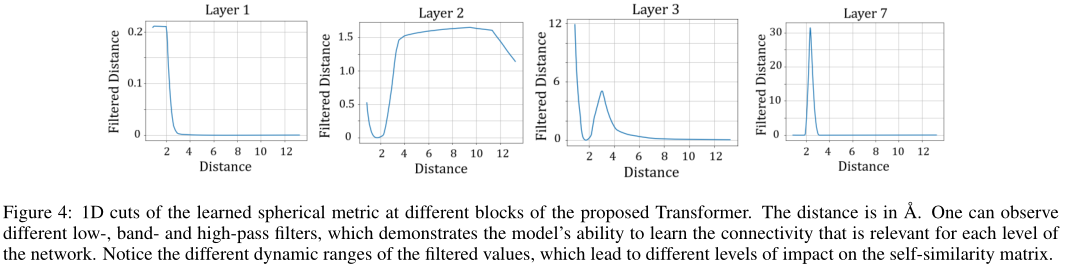
现有的很多方法都很难对交互功能ψω建模。从力场方法到最近的基于学习的方法,需要经验地重新定义欧几里得成对距离,以便满足物理定律。通常情况下,这些方法中存在的最关键的超参数之一是截止距离。 在这里,作者建议学习在transformer的每个级别的成对距离ψω。通过ψω对距离进行变换与自注意力机制相结合,使得能够根据预测目标直接优化原子间的距离表示以及截止距离,消除了繁琐的超参数,允许以自适应方式进行学习。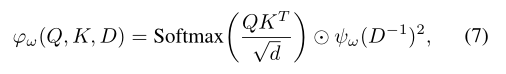
Regularization via Molecule Augmentation
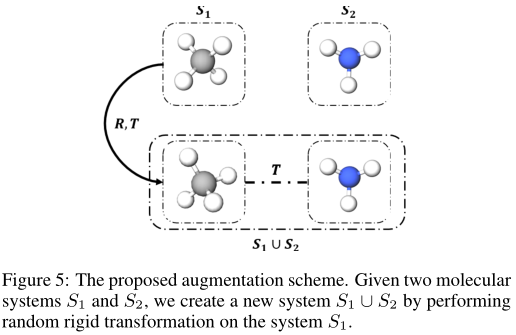
transformer一般都是非常大的、过度参数化的模型。减少过拟合的最有效技术之一是数据增强。然而,增加分子数据并不简单,特别是对于回归任务,因为修改一种原子类型或其空间位置会对分子性质产生不可预测的影响。混合策略从成对(或更多)的数据中创建新的样本。在这里,根据最初的距离相关性假设,作者建议将混合策略思想扩展到分子,通过创建由两个相距较远的分子组成的系统来获得新的样本。作者将新系统的性质定义为两个分子的性质之和。模型计算得到的原子之间的注意力分数使得模型能够学习如何将两个相距较远的子系统分开,并减少过拟合。如下图所示,新系统定义为两个分子经过旋转平移之后的组合:
3 实验
Dataset
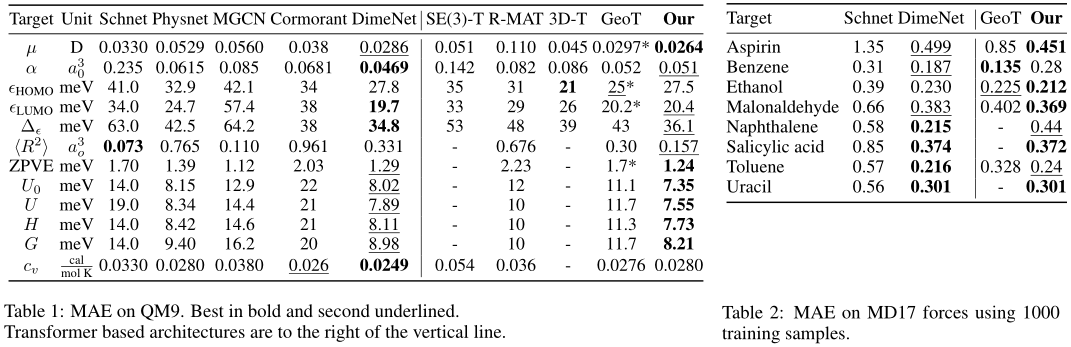
在table 1(左)中,显示了模型在QM9数据集上的平均绝对误差(MAE);在table 2(右)中使用MD17来测试分子动力学模拟中的模型性能:
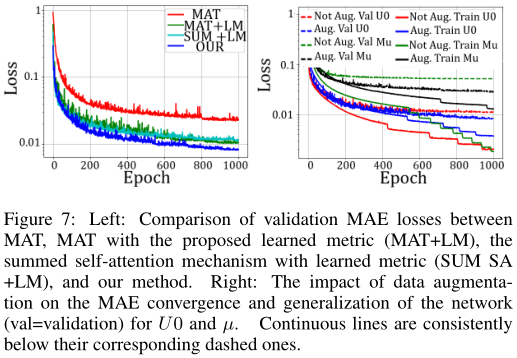
Comparison and Ablation Studies
比较了不同自注意模块的影响。给出了方法的收敛曲线,如Figure 7(左)所示。同时给出了训练过程中数据增强对模型泛化的影响。Figure 7(右)显示了对于属性U0和µ,数据增强对模型收敛的影响。可以看出,在这两种情况下,当应用数据增强时,训练集和验证集之间的泛化差距被极大地减小: