《基于博弈论的小规模战斗战术分析》400页

武装冲突中的优势不仅来自于能力或数量上的优势，还来自于资产的使用方式，小到单个车辆和弹药的操作。本文件概述了一项研究计划，重点是针对军事相关场景的小规模战术。小规模交战指的是交战双方的规模--一般是一个对一个、两个对一个和/或一个对两个--以及每个小组的目标或目的都已明确这一事实。问题领域包括追击-规避和目标守卫，其中任何一个都可视为空对空作战、地面资产压制/防御等军事任务中的子问题。在大多数情况下，所考虑的战术包括智能体的控制策略（即其空间机动），但也可能包括角色分配（例如，是充当诱饵还是前锋）以及离散决策（例如，是交战还是撤退）。小规模冲突的战术非常重要，因为它们可以帮助我们了解如何处理更大规模的冲突（多对多、多目标、多决策）。强化学习和神经网络等机器学习方法已被证明能够为大型智能体团队开发控制器。然而，与最优（或均衡）策略相比，这些控制器的性能通常是未知的。微分博弈论以鞍点平衡控制策略和零和博弈中的最小（或最大）成本/回报的形式，为相关情景提供了严格的解决方案。当平衡控制策略可以通过分析获得时，它们就适合机载/实时实施。本文探讨了与经典微分博弈论方法相关的一些挑战。出现这些挑战的主要原因是奇异性的存在，即使是最简单的微分博弈也可能出现奇异性。在** (i) 多追兵、单逃兵微分博弈、(ii) 多智能体炮塔防御场景和 (iii) 交战或撤退场景**中，演示了小规模解决方案的实用性。最终，这项研究成果为新型场景提供了微分博弈和最优控制解决方案、计算奇异曲面的数值技术、计算密集型解决方案的近似值，以及处理具有多个阶段或结果的场景的技术。

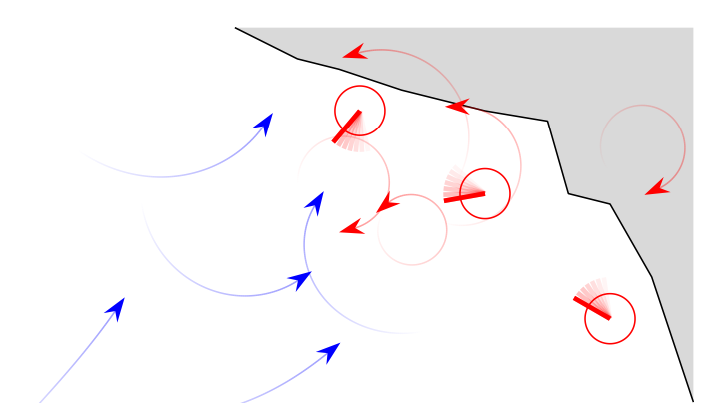
图 1.2：蓝队与红队冲突的概念图。红队除了移动智能体外，还有 3 个炮塔。灰色区域可能代表蓝队的目标区域--他们可能希望撤退到那里，或者进入该区域造成破坏或寻找特定目标。当然，在尝试计算各种智能体的控制权之前，可以先考虑它们之间的分配；但即使是这样，也可能取决于每个团队更高层次的任务目标。例如，红队可能希望尽量减少人员伤亡，或尽量减少进入灰色区域的蓝方智能体数量。

对抗性冲突中的战略范围很广，从军事条令到自然生物的行为和适应。在无数的应用领域（如军事、生物、经济、游戏、体育等）中，可以在许多层面上构想战略或战术--从组织层面（即实体群体之间的合作）到个人层面（飞行员、动物、投资者等的决策）。此外，对手不可预测的行动和反应也始终是一个挑战。我们可能会费尽心思去了解冲突的背景或环境、对手的能力，甚至对手当前的状态。然而，最终冲突的结果通常取决于对手现在和将来会做什么。

本研究关注的是小规模冲突层面的战略战术，重点是与军事相关的场景（不过，最终应用的大部分现实情况都将从分析中抽象出来）。"小规模冲突"一词没有精确的数学定义，但在整个分析过程中被用来表示小队智能体之间的冲突，包括一对一（1v1）冲突。大部分分析集中于 1v1、2v1、1v2 和 Mv1 冲突。除了小规模的团队外，小规模冲突还意味着可以将场景归结为每个团队的特定目标。这与规模更大、范围更广的冲突形成鲜明对比，例如，军事任务可能由许多子任务或子目标组成，甚至是由跨越各种资产的许多任务组成的军事战役。

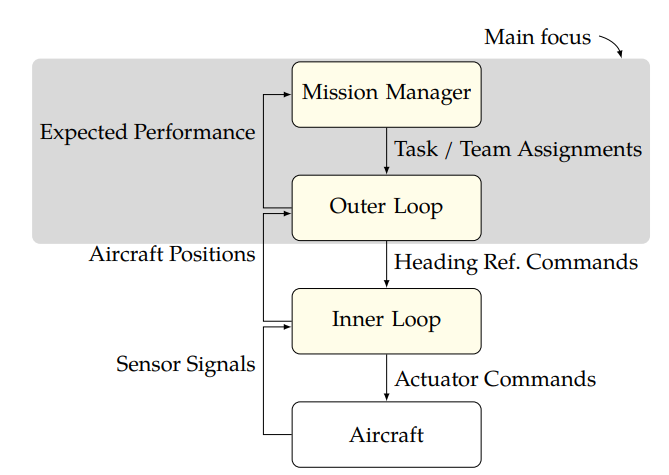
关注的两个主要问题领域是追击-规避和目标防护。在前者中，一个追击者（或一组追击者）试图捕获一个规避者（或一组规避者）。在后者中，防御者试图阻止攻击者到达一组目标状态，这组目标状态可能代表感兴趣的区域或移动智能体的位置。请注意，在本文档的其余部分中，将遵守智能体名称大写的惯例。对于这两个问题领域，主要关注的是智能体的空间机动性。图 1.1 显示了智能体（如飞机）内部各层自主（或自动）控制之间的概念关系。如图所示，本文提出的研究主要涉及最上两层：任务管理器和外循环。例如，本文提出的分析和算法可能会根据 "高层 "决策（如飞机应完成的任务）或以 "高层 "决策为前提，为飞机规定航向参考指令。假定存在一个 "低级"（内环）控制器，该控制器向飞机发送执行器指令，以跟踪外环提供的参考指令。反过来，内环向外环提供飞行器状态信息（如位置）。外循环提供分配任务的性能估计值，任务管理器利用该估计值来评估是否进行更新，例如重新分配任务或重新组建团队。在追击-规避和目标防护方面，任务管理器的可能功能包括为飞行器分配角色或分配任务，例如为追击者分配特定的 "规避者 "作为目标。其他可能的角色包括：充当诱饵，以吸引队友的注意力；充当前锋，瞄准目标；或充当阻挡者，以防止切断对手的某些路径等。此外，任务管理器还可能负责做出不连续的决定，例如攻击者是否应该与防守者交战或完全撤退。

图 1.1：描述自主飞行器等控制层的概念框图。

更大、更复杂的冲突可能涉及更大的智能体团队（即多对多）、许多不同的目标和许多不同的决策。此外，冲突的结构可能会随着时间的推移而改变。图 1.2 展示了这样一个冲突的抽象例子，冲突发生在由 5 个移动智能体组成的蓝队和由 5 个移动智能体与 3 个炮塔组成的红队之间。作为人类，如果我们能理解并推理出每场小规模冲突中的最优方案，我们就更有可能理解更大规模的交战。

微分博弈论（DGT）提供了一种定量分析智能体表现的机制，同时还能让我们深入了解智能体之间的潜在互动。在 DGT 中制定的问题解决方案由每个参与者的鞍点均衡策略以及价值函数组成，后者代表了作为系统状态函数的冲突均衡结果。这些鞍点解决方案非常强大，因为它们向每个玩家保证，如果他们执行均衡策略，无论对手采取什么行动，他们的结果都不会比博弈值差。

拟议的研究计划可概括为：获取新颖小规模对局的微分博弈解，将现有解扩展到更复杂的小规模对局，开发/比较数值技术，以及开发近似解。在整个计划中，重点是微分博弈和最优控制解决方案的实际应用--目标是使单个智能体能够利用机载计算资源，在适合特定任务的时间内计算出其最优/均衡控制输入。因此，我们的目标通常是获得这些问题的闭式解析解。如果无法做到这一点，也可以开发维度更小的参数解，并使用传统的寻根方法快速高效地求解。最后，当解析解和参数解都不可行时，就需要寻找合适的近似解。

在下一节中，将使用 DGT 提出并求解一个经典的追逐-规避场景，其中涉及一个追逐者和一个规避者，以介绍一些关键概念，如参与者、成本函数、控制变量、均衡和价值。第 2 章包含文献调查，为拟议的研究提供必要的背景并确定关键主题。第 3 章将拟议计划具体化为一系列研究目标；最后讨论了所采用方法的挑战和优势。