《下马作战模型中的通信和态势感知分析》92页技术报告（含源码）

引言

专门用于下马士兵系统的国防资金是有限的，而且必须在多个部分之间进行分配。决定正确的组合可能是困难的--一些技术提高了杀伤力和保护力，另一些则提高了安全性能。同时，这些技术可能会增加认知和身体负荷。本报告提出了一种方法来进行跨越这一明显的鸿沟，并找到技术的最佳组合。提出了一个数学战斗模型，该模型考虑了态势感知、杀伤力和保护设备在预期挽救生命方面的联合效应。因此，该模型可以用来设计一个最佳的下马士兵系统，一个可以拯救人生命的系统。

模型

本方法依赖于在任何时候都将决策者表现为一个最佳的决策者。然而，该决策者必须在不确定性和时间限制下做出决定。随着认知负担的增加，模型中可能会发生几个变化：决策之间的时间可能会增加，每个决策中考虑的信息量可能会减少，或者规划范围可能会缩短，导致更多的短视决策。模型中的每一个杠杆都能灵活地代表决策的退化，以及SA，同时仍然假设指挥官是在做出尽可能好的决策，但在困难的约束下。在技术上，我们的模型是基于两个支柱。首先，战斗被建模为连续时间马尔可夫链（CTMC）。其次，指挥官被模拟为部分观测马尔可夫决策过程（POMDP）中的决策者。POMDP是通过动态规划解决的顺序决策问题。它们很难解决，因为与完全可观察的马尔可夫决策过程（MDPs）相反，一些状态变量是隐藏的。幸运的是，先进的计算方法已经被开发出来以解决它们。

结果

本文实施了一个概念验证，基于一个下马的战斗场景，其中一个由12名士兵组成的小组必须确保一个隧道的入口。在任何时候，指挥官都可以根据当时的信息改变路线，或放弃行动。在这个场景中，还包括一个区域传感器，例如，它可以是一个无人驾驶飞行器（UAV）。展示了如何在增加士兵的传感能力和增加无人机的能力之间找到最佳权衡。还展示了如何在增加士兵的感知能力和增加他们的杀伤力和个人保护设备之间找到最佳的平衡。最后，展示了如何通过增加模型中决策的时间间隔，来模拟认知负担的增加，从而增加预期的生命风险。

结论

该模型在采购、能力发展、国防科技和学术领域具有开发潜力。这种广泛的潜力要归功于POMDPs的灵活性，它可以根据需要做得很抽象，或者很详细。提出了几个扩展模型实现的途径：整合贝叶斯信念网络（在CTMC和/或观察模型中），结合情景阶段的序列，并探索其他表示认知负担的方法。

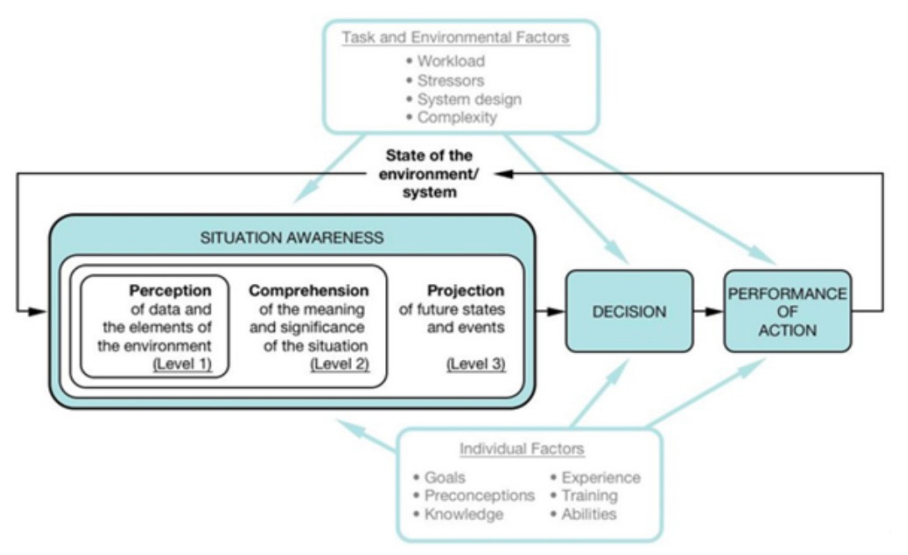
图 2-1：战斗中SA的概念概述。