【ICML2023】MetaModulation: 用更少任务进行小样本学习的变分特征层次结构学习

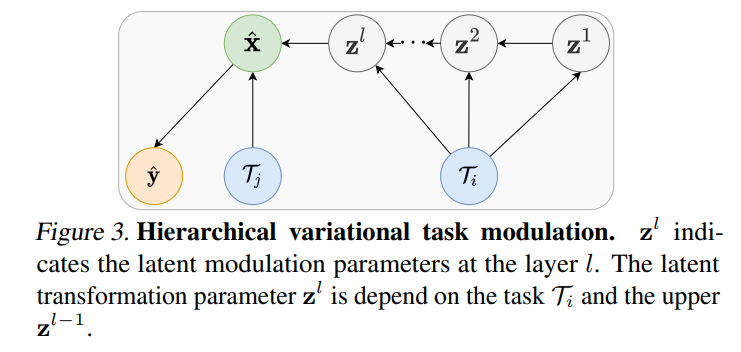
元学习算法能够利用先前学习的知识来学习新任务，但它们通常需要大量的元训练任务，而这些任务可能并不容易获得。为了解决这个问题，我们提出了一种用更少任务进行小样本学习的方法，我们称之为 MetaModulation（元调制）。关键的想法是通过在元训练期间调节批量归一化参数，使用神经网络增加元训练任务的密度。此外，我们在各种网络层面，而非仅在单一层面，修改参数以增加任务多样性。为了解决由于训练任务有限而导致的不确定性，我们提出了一种变分元调制方法，其中调制参数被视为隐变量。我们还引入了通过变分元调制学习的变分特征层次结构，这种调制可以调节所有层面的特征，并能考虑任务不确定性，生成更多样化的任务。消融研究显示了在不同层面利用可学习的任务调制的优点，并证明了在少任务元学习中加入概率变体的好处。我们的元调制及其变分变体在四个少任务元学习基准测试中均一致优于当前最先进的替代方案。

https://www.zhuanzhi.ai/paper/6bad681ebd0c520eacc14067e18627dc