Correction of overfitting bias in regression models

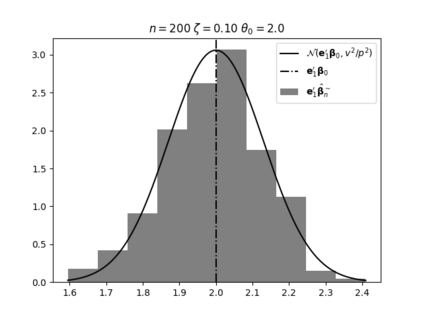
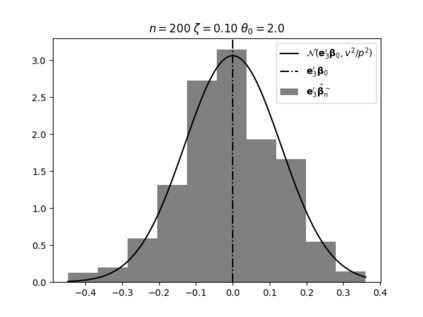
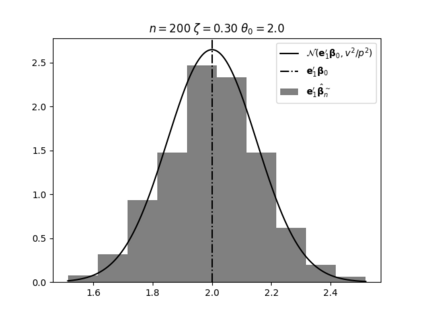
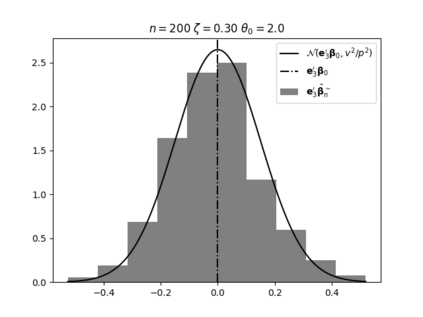
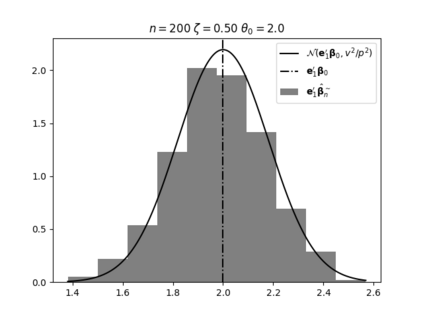
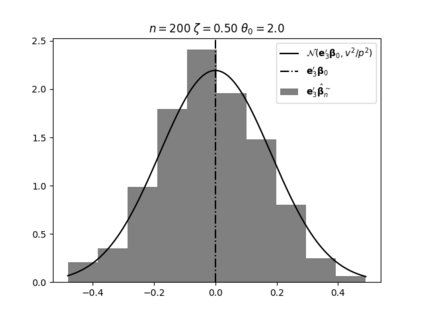
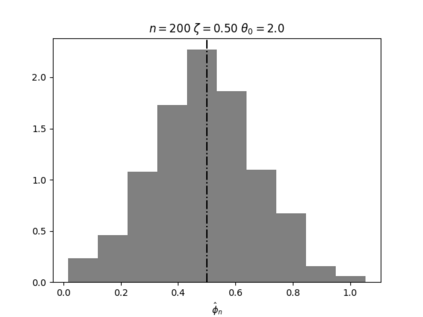
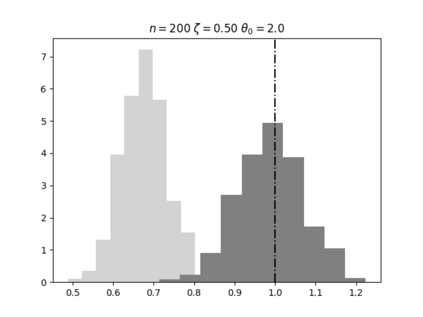
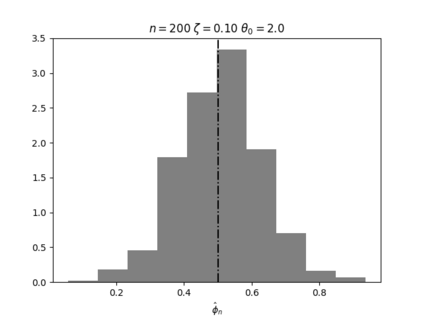
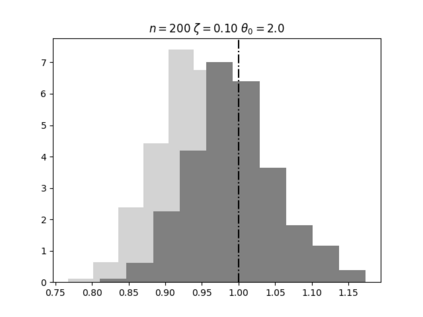
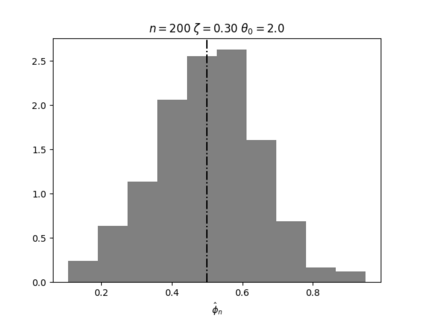
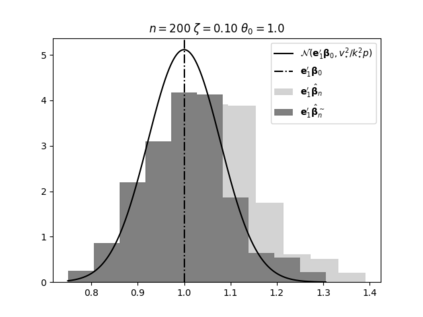
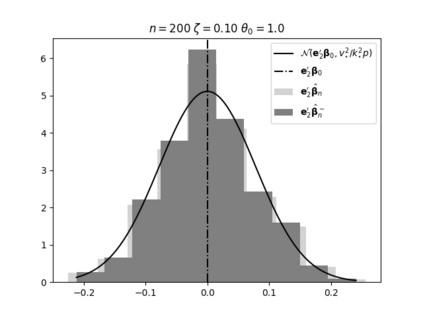
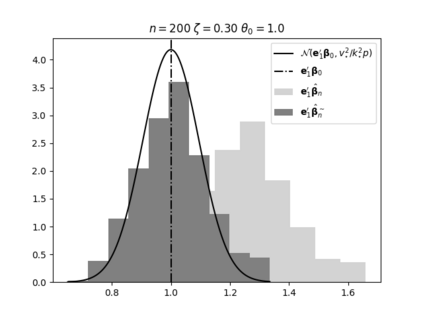
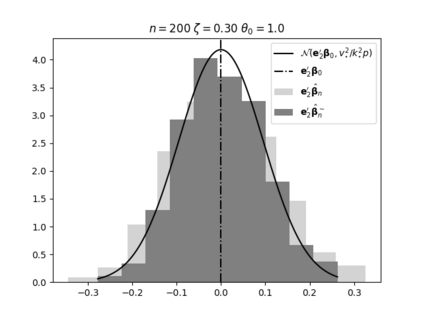
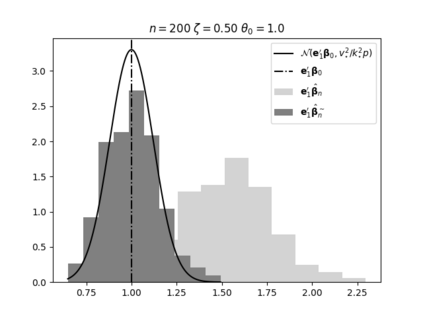
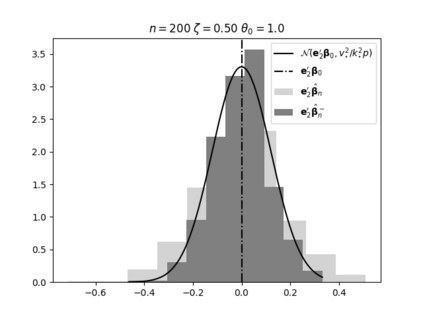
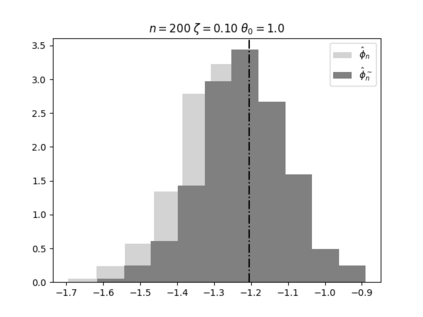
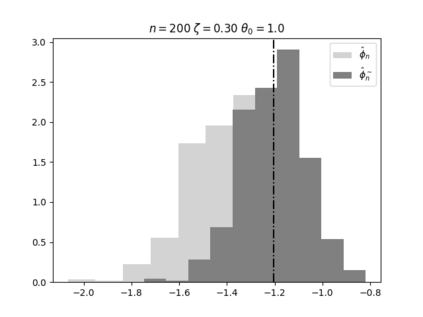
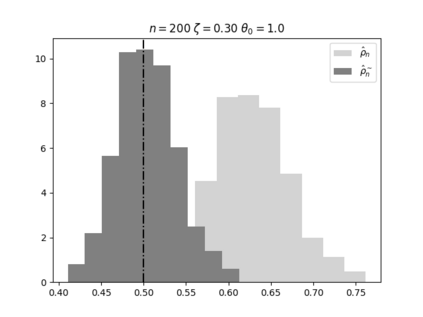
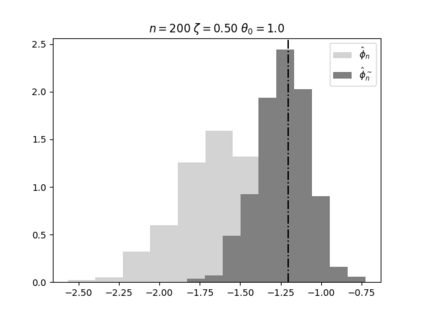
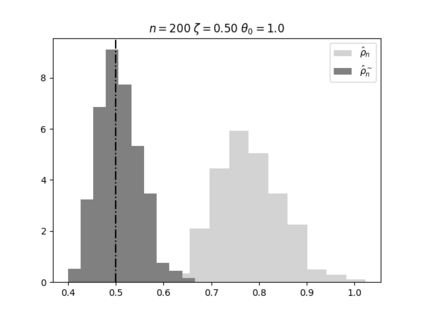
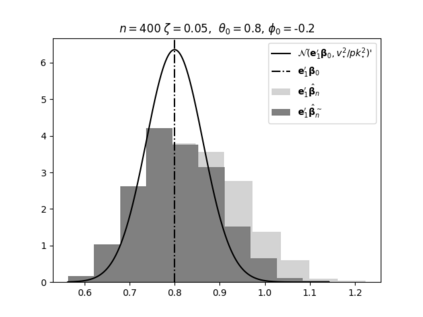
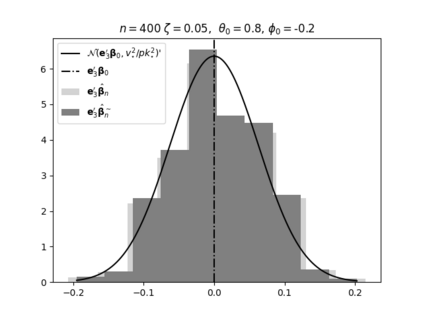
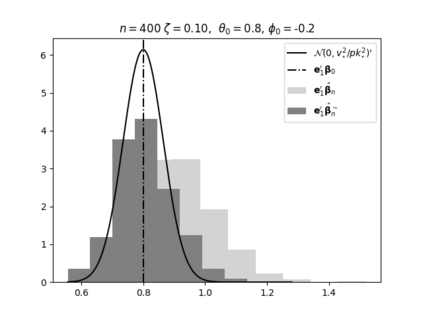
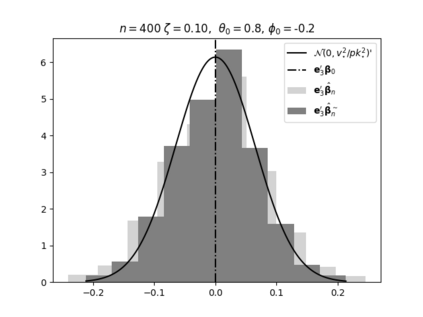
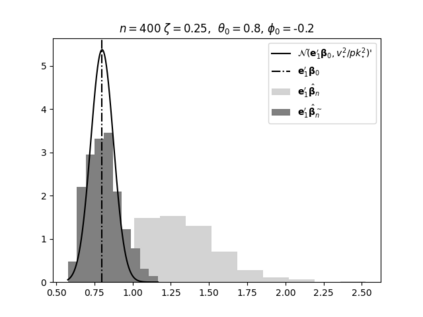
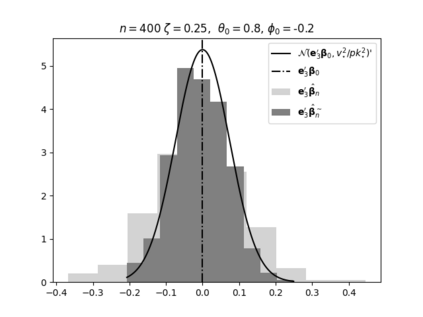
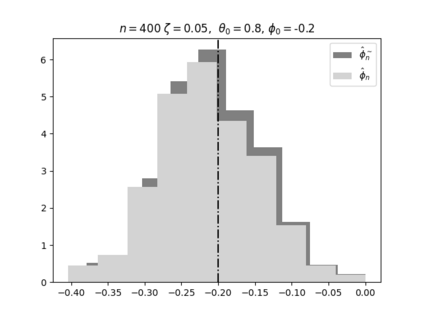
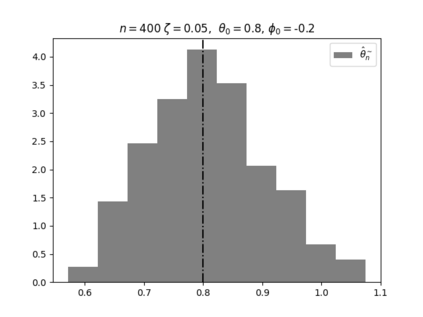
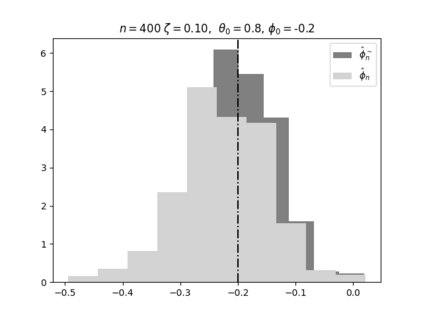
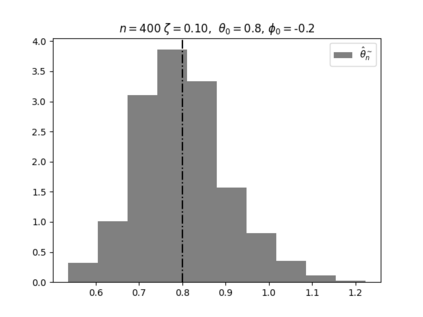
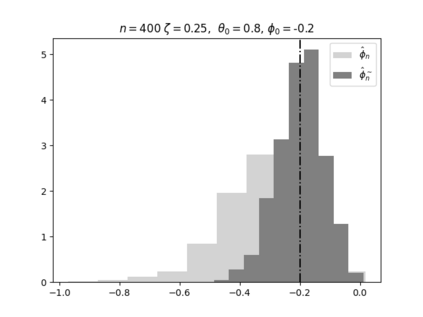
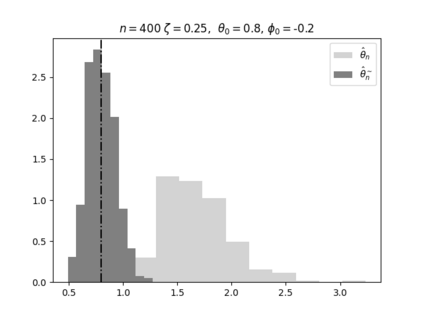
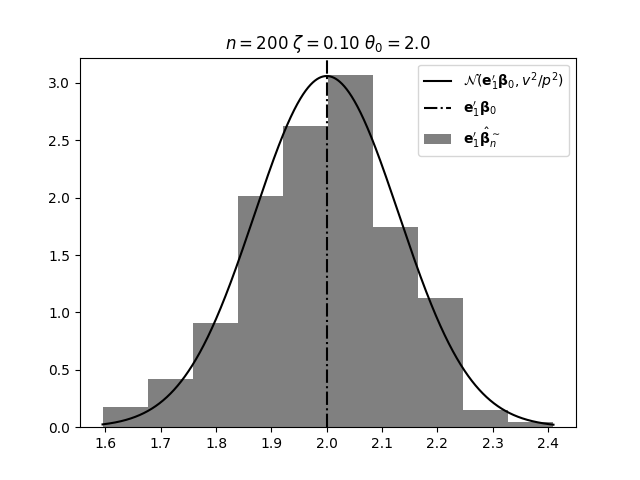
Regression analysis based on many covariates is becoming increasingly common. However, when the number of covariates $p$ is of the same order as the number of observations $n$, statistical protocols like maximum likelihood estimation of regression and nuisance parameters become unreliable due to overfitting. Overfitting typically leads to systematic estimation biases, and to increased estimator variances. It is crucial to be able to correctly quantify these effects, for inference and prediction purposes. In literature, several methods have been proposed to overcome overfitting bias or adjust estimates. The vast majority of these focus on the regression parameters only, either via empirical regularization methods or by expansion for small ratios $p/n$. This failure to correctly estimate also the nuisance parameters may lead to significant errors in outcome predictions. In this paper we use the leave one out method to derive the compact set of non-linear equations for the overfitting biases of maximum likelihood (ML) estimators in parametric regression models, as obtained previously using the replica method. We show that these equations enable one to correct regression and nuisance parameter estimators, and make them asymptotically unbiased. To illustrate the theory we performed simulation studies for multiple regression models. In all cases we find excellent agreement between theory and simulations.