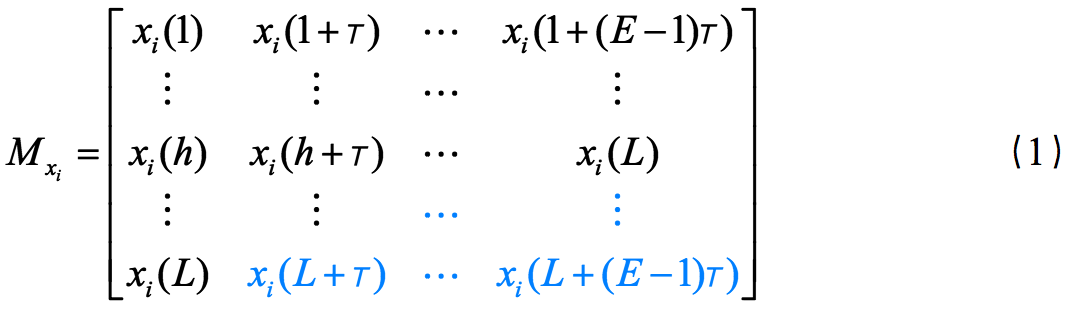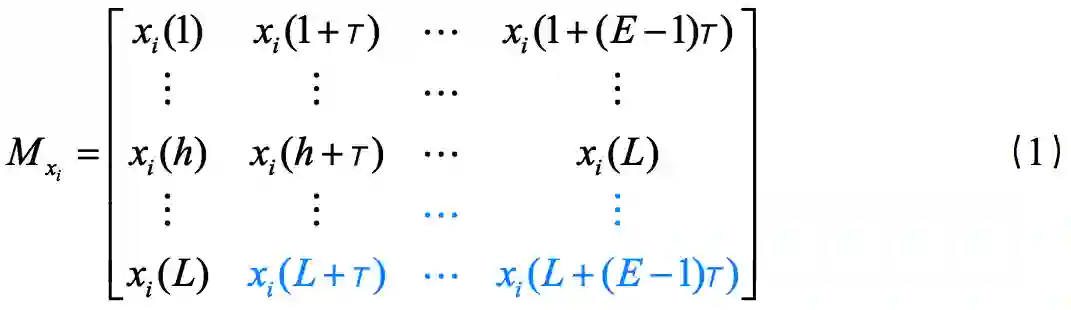Nat. Commun.前沿：数据驱动的复杂系统预测

导语

近日，成都理工大学管理科学学院伍涛研究员，与中国地质大学（北京）经济管理学院安海忠教授、高湘昀教授、北京化工大学经济管理学院安峰副教授、美国伦斯勒理工大学高建喜副教授以及德国洪堡大学Jürgen Kurths教授等合作者，在《自然·通讯》杂志上发表题为《Predicting multiple observations in complex systems through low-dimensional embeddings》的研究论文，提出了一套基于流形嵌入理论和延迟嵌入理论的预测模型，实现对复杂系统内所有变量提前多期的预测。本文是论文的第一作者伍涛对该项研究的解读。

研究领域：复杂系统预测，时间序列，流形嵌入理论，延迟嵌入理论**************************************************************** 伍涛 | 作者

---

论文题目：Predicting multiple observations in complex systems through low-dimensional embeddings论文作者：伍涛，高湘昀，安峰，孙笑甜，安海忠，苏臻，Shraddha Gupta，高建喜，Jürgen Kurths论文链接：https://www.nature.com/articles/s41467-024-46598-w

数据驱动复杂系统预测进展与挑战

现实社会中存在诸多复杂系统，例如气候系统、金融系统、交通系统等。对现实复杂系统未来的演化进行提前准确的预测对指导决策具有重要的现实意义，也是各学科领域长期关注的重点问题。对于实际复杂系统，若能找到描述系统的动力学微分方程，则预测问题相对容易。然而，实际系统内在机制过于复杂，很难用一组或者多组微分方程刻画系统的演化动力学。尽管无法获知系统的演化动力学，但系统随时间的演化产生的时间序列是可获得的，从时间序列出发预测系统未来的演化是有效的途径之一，即数据驱动的复杂系统预测。 数据驱动的复杂系统预测问题已经展开了很多启发性的研究，产生了众多预测方法，其中代表性的方法如随机分布嵌入模型（RDE）[1]和自动存储神经网络（ARNN）[2]等。这些方法实现了对复杂系统的单步预测和多步预测等任务。 现实系统往往包含众多变量，例如气候系统包含众多具有时空特征的观察变量，大脑包含成千上万相互关联的神经元。对于系统内所有变量的预测有助于预测整个系统未来的演化。针对该问题，虽然已有一些研究，但仍面临以下挑战： （1）预测因子不确定性，对系统内不同的待预测对象，现有研究通常采用不同的预测因子，例如选取与被预测变量相关性高的变量作为预测因子；（2）预测模型不确定性，对于系统内不同待预测变量采用不同的预测方法，对于N-维系统可能选取N个不同的预测模型；（3）方法有效性，现有大多数预测方法的有效性仅在系统内少量变量中得到验证。因此，亟需一个可靠的模型对复杂系统内所有变量进行预测。

模型构建：流形学习嵌入与延迟嵌入

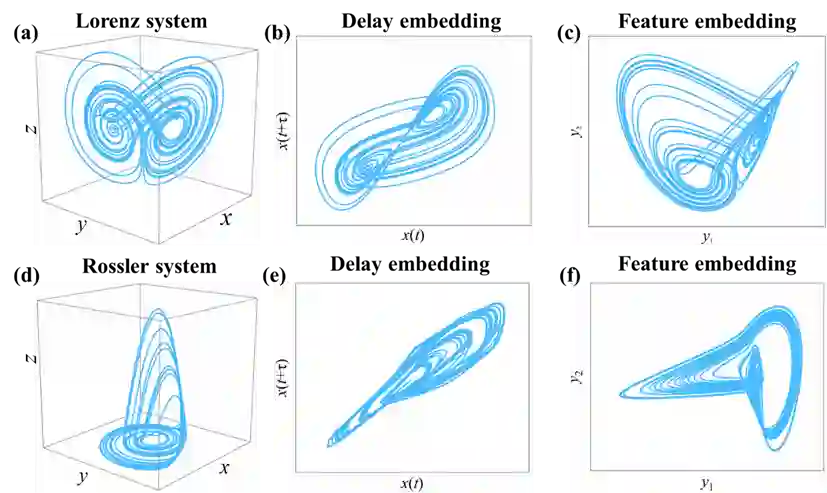
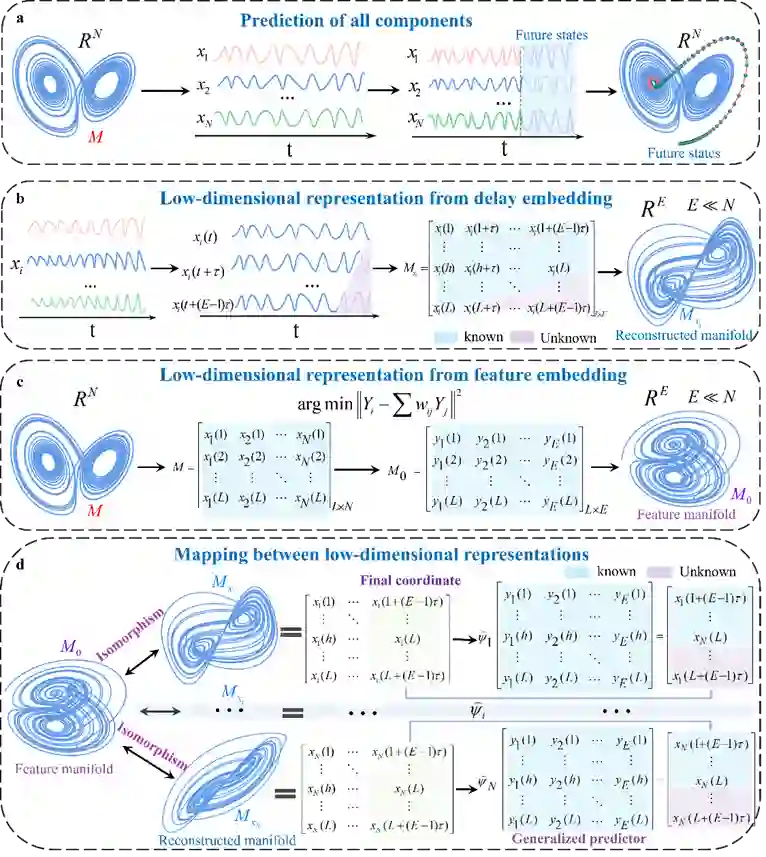
面对实际高维系统，传统的预测方法面临维数灾难，而提取高维系统动力学特征，将高维系统降维到低维空间是应对维数灾难有效的途径。动力系统（N-维）随时间的演化产生诸多时间序列数据。根据Takens延迟嵌入定理，选取合适的嵌入维数E和时间延迟T，动力系统内任意变量的时间序列都可以用来重构与原始系统拓扑等价的动力学结构，并且重构的动力学结构（如公式（1）所示）往往处于低维空间中，即E＜＜N。因此，通过延迟嵌入定理，高维系统动力学拓扑特征可以被等价地表示在低维空间中。以经典的3-维Lorenz系统和3维Rössler系统为例，由各自系统内变量的时间序列可以在2-维空间中重构出与原始系统等价的动力学结构，如图1（a），（b）,（d）和（e）所示。

另一方面，根据Whitney嵌入定理，高维系统往往是冗余的，其核心特征存在于一个低维的流形上。基于此定理，可以构建一个一一映射，保留系统拓扑特征（例如，原始系统在空间中相邻的点，在嵌入的低维空间中也相邻），将高维系统映射到低维空间中，而这个过程可以通过流形学习算法实现。例如，通过流形学习算法（Diffusion map），3维Lorenz混沌系统和3维Rössler混沌系统的拓扑结构可以被表示在2维空间中，如图1（c）和（f）。 图1. 复杂系统的低维嵌入 由上述分析可知，通过延迟嵌入定理和流形学习算法，高维系统的拓扑特征可以被两种不同的方式表示在低维空间中（降维后的分别称为重构流形和特征流形）。重构流形和特征流形都与原始系统具有等价的拓扑结构，因此可以构建从特征流形到重构流形的一一映射。高维系统的特征流形由流形学习算法得到，故特征流形上所有点的状态可以由流形学习算法确定，而延迟嵌入得到的重构流形上部分点的状态是未知的（公式（1）中蓝色元素），这些未知元素代表变量未来的值，正是需要预测的值。由于动力系统内任意时间序列都可以构建重构流形，故可以将特征流形作为通用的预测因子，通过构建从特征流形到重构流形的映射（由高斯过程回归确定），实现对系统内所有变量的预测，如图2所示。 图2 “特征流形-重构流形映射”预测方法框架图

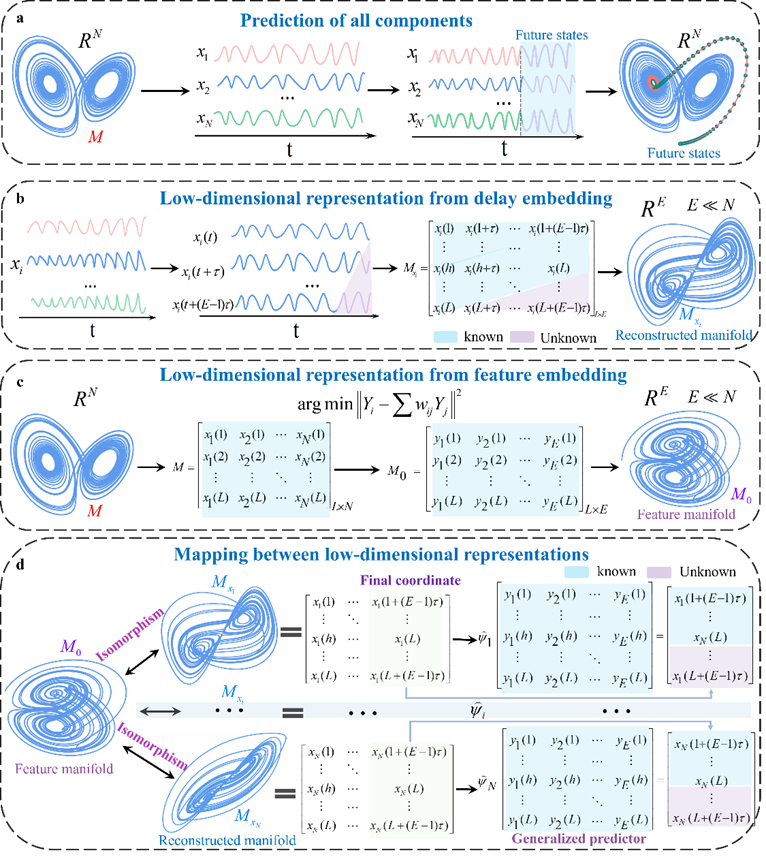
主要结果

选取耦合的Lorenz系统作为代表性的模拟系统，实现了对该系统内所有变量提前多期的准确预测。然后，分别选取气候系统，神经系统，金融系统，交通系统验证了本文模型的有效性。接着，对模型参数、噪声等进行讨论，验证了模型的稳健性。最后，与经典的预测模型进行对比，本文的模型对于少训练样本且多测试样本具有更高的稳健性。

结论与展望

本文基于延迟嵌入理论和流形嵌入理论，将高维系统的核心拓扑特征嵌入到低维空间中，构建从特征流形到重构流形的映射，实现对复杂系统内所有变量提前多期的预测。本文构建了一个通用的预测框架，其中特征流形作为通用的预测因子，高斯回归算法作为通用的训练算法，克服了预测因子和预测模型选择不确定性的困难。此外，方法的有效性通过对系统内所有变量的预测得到验证。 然而，本文的方法也存在以下局限性，对每一个待预测变量需要进行一次实验，无法同时对系统内所有变量进行预测；其次，当系统出现突变特征时，系统动力学规则发生较大变化，本文的模型难以实现准确的预测。

主要参考文献[1] Ma, H. F., Leng, S. Y., Aihara, K., Lin, W. & Chen, L. N. Randomly distributed embedding making short-term high-dimensional data predictable. PNAS. 43, E9994-E10002 (2018).[2] Chen, P., Liu, R., Aihara, K. & Chen, L. N. Autoreservoir computing for multistep ahead prediction based on the spatiotemporal information transformation. Nature Communications. 11, 4568 (2020).