【NeurIPS2020-北大】非凸优化裁剪算法的改进分析

Improved Analysis of Clipping Algorithms for Non-convex Optimization

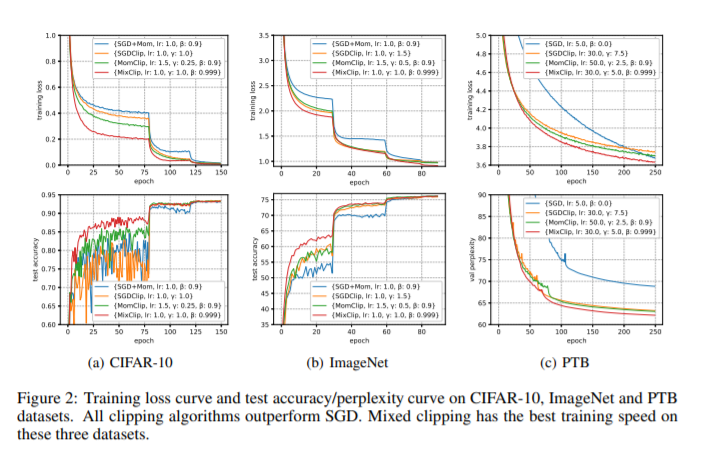
梯度裁剪在深度神经网络训练中应用广泛，部分原因是其在解决梯度爆炸问题上的实用性。最近，Zhang等人[2020a]通过引入一个新的假设(L0, L1)-平滑性，证明剪切(随机)梯度下降(GD)比普通的GD/SGD收敛得更快，该假设表征了深度神经网络中通常遇到的梯度剧烈波动。然而，它们在问题相关参数上的迭代复杂性是相当悲观的，并且裁剪与其他关键技术(如动量加速)相结合的理论证明仍然缺乏。在本文中，我们提出了一个研究剪切算法的一般框架来弥补这一差距，该框架也考虑了动量法。我们提供了框架在确定性和随机设置的收敛性分析，并通过比较它们与现有的下界来证明我们的结果的紧密性。我们的结果表明，剪裁方法的效率不会退化，即使在景观的高度非光滑的区域。实验证明了基于裁剪的方法在深度学习任务中的优越性。

https://arxiv.org/abs/2010.02519