摘要
自2017年引入以来,物理信息神经网络(PINNs)已成为科学机器学习中的关键工具,使得利用稀疏测量高效求解常微分方程和偏微分方程成为可能。近年来,PINNs在训练和优化方面取得了显著进展,包括网络架构、自适应细化、域分解,以及自适应权重和激活函数的使用。一个显著的近期发展是物理信息Kolmogorov–Arnold网络(PIKANs),该网络利用了Kolmogorov在1957年提出的表示模型,为传统PINNs提供了一种有前景的替代方案。在本综述中,我们全面介绍了PINNs的最新进展,重点关注网络设计、特征扩展、优化技术、不确定性量化以及理论见解的改进。我们还概述了其在多个领域中的关键应用,包括生物医学、流体和固体力学、地球物理学、动力系统、热传导、化学工程等。最后,我们回顾了由学术界和工业界开发的支持PINN研究和应用的计算框架和软件工具。
关键词:物理信息神经网络;Kolmogorov-Arnold网络;优化算法;可分解的PINNs;自适应权重;不确定性量化
1. 引言
有限元方法(FEM)在过去几十年里一直是计算科学与工程(CSE)的基石,但在20世纪60年代初期首次发表相关研究时曾受到质疑。尽管FEM在学术研究和工业应用中取得了成功,但除非使用复杂的数据同化方法,否则FEM无法轻易整合测量数据,使得大规模计算成本高昂。FEM和其他传统数值方法在解决已知边界和初始条件以及所有材料参数的良定问题上效果显著。然而,在实际应用中,这些条件往往存在缺漏,因此需要做出任意假设。例如,在功率电子冷却应用中,需要假设墙壁的热边界条件。这可能导致错误的结果,因为在此类问题中,关注点通常是位于表面的最高温度或最高热流,而错误的假设恰恰应用于此类区域。相反,可用的可能只是一些稀疏的测温数据,无论是在表面上还是在感兴趣区域内部。不幸的是,当前的数值方法(如FEM)无法有效利用这些测量数据,从而导致系统的关键实验信息丢失。另一方面,神经网络基于任何精度或模式的数据进行训练,因此数据同化在此设置中是一个自然过程。
物理信息神经网络(PINNs)正是为了满足这一需求而开发的,考虑了模拟场景中的部分已知物理定律,但并非完整知识,且对某些状态变量存在稀疏测量,而非全部。因此,PINNs为将物理定律编码到神经网络中提供了一个框架【1】,并弥合了传统物理模型和现代纯数据驱动方法之间的脱节。具体而言,PINNs通过在目标函数中加入一个额外的“残差”损失项,将底层偏微分方程(PDE)作为软约束纳入其中。PINNs在所有科学领域中都能够有效解决正向和反向问题。它们可以结合稀疏和噪声数据,因此在获取准确测量结果困难或昂贵的情况下尤为有效。PINNs的一项关键创新是基于计算图的自动微分的使用,使其能够精确处理守恒定律中的微分算子,并且消除了耗时且限制解精度的网格生成需求。
自2017年在arXiv上出现的两篇原创论文【2, 3】以及2019年随后的联合出版论文【1】以来,CSE社区充满了兴奋,来自全球各科学领域的研究团队提出了许多关于该方法不同方面的重要改进。在撰写本文时,论文【1】的引用量已超过11000次,许多研究探讨了PINNs在不同科学领域的适用性,同时提出了算法改进以应对原始设计的局限性。在本综述中,我们汇编了大多数主要的算法开发成果,并列出PINNs在不同学科领域的广泛应用。附录中展示了一些关于PINNs的重要文献时间线,从PINNs【2】到PIKANs【4】。
现有的综述,如【5-8】,总结了PINNs的关键方面,而本文的不同之处在于我们对最新的算法进展进行了更广泛的概述,并涵盖了PINNs在更多科学学科中的应用。综述【5】和【6】主要关注PINNs在各领域的方法和应用,较少强调最近的算法改进。综述【8】简要概述了PINNs及其扩展,并以数据驱动的方程发现为例,但并未深入探讨PINNs的应用。综述【7】则包括了算法发展的讨论,但其应用范围局限于热管理和计算流体力学。此外,一些综述聚焦于特定应用领域。例如,【9】和【10】回顾了PINNs在流体动力学中的应用,而【11】则专注于电力系统的应用。相较之下,【12】进行了120篇研究论文的文献计量分析,突出了PINNs研究中的主要出版趋势、高被引作者和主要国家。
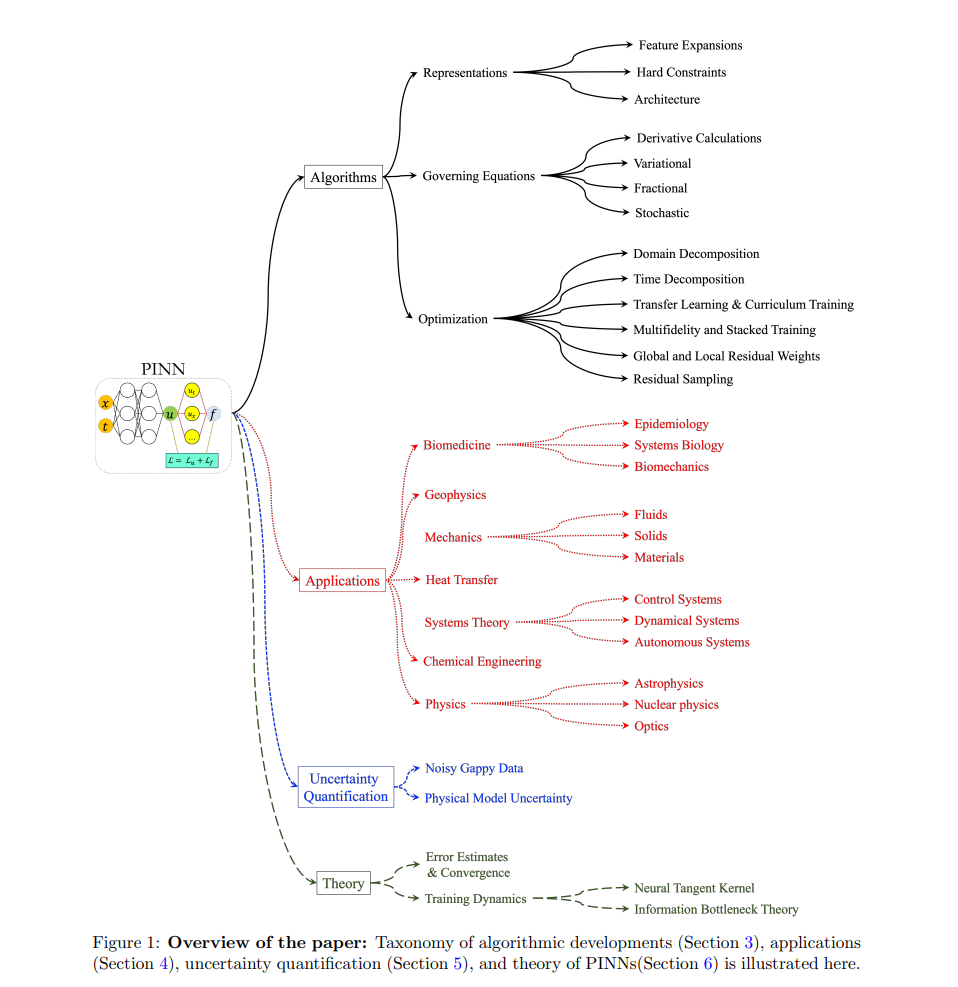
本文的结构如图1所示。在第2节中,我们概述了物理信息机器学习的一般框架。第3节对旨在改进PINNs的主要技术进行了全面总结。第4节概述了PINNs的多样化应用。第5节重点介绍了PINNs中的不确定性量化方法。第6节总结了PINNs背后的理论发展。第7节回顾了各种计算框架和软件。最后,在第8节中,我们提供了讨论和未来展望。
2. 物理信息机器学习(PIML)
物理信息机器学习(PIML)已成为求解正问题和逆问题中偏微分方程(PDEs)的传统数值方法的强大替代方案。PIML最早由Raissi、Perdikaris和Karniadakis在一系列论文中提出【13】,基于高斯过程回归(GPR);另见同一作者的专利【14】。然而,本文将回顾PIML利用神经网络和自动微分的后续发展,起始于2017年在arXiv上的两篇论文【2, 3】,随后于2019年合并为一篇论文【1】。值得注意的是,早期论文【15, 16】尝试求解PDE(正问题),但未进行数据融合或自动微分。本文介绍的PIML采用表示模型,如多层感知器(MLP)或Kolmogorov-Arnold网络(KAN)【4】,以最小化包含多项的损失函数来逼近常微分方程(ODEs)或偏微分方程(PDEs)的解,并符合给定的数据和约束条件。特别地,该损失函数旨在拟合可观测数据或其他物理或数学约束,同时满足底层物理定律,例如守恒定律【1, 17】。
与传统数值方法不同,大多数PIML模型不依赖于预定义的网格或网格划分,从而能够高效处理复杂几何和高维问题。通过自动微分,PIML模型无需离散化即可准确计算导数,将物理定律与数据无缝整合。这种灵活性使PIML模型能够利用部分信息来逼近解,非常适合揭示隐藏参数【1】,以及从现实世界数据中重建【18】或推断隐藏场【19】。此外,PIML模型在处理高维PDE【20】、耦合系统【21, 22】、随机微分方程【23】和分数阶PDE【24】方面表现出色,同时通过在现代硬件(如GPU)上的并行化实现了可扩展性【25】。这使得PIML模型能够以较低的计算开销高效处理多物理问题和大规模模拟,相比传统方法更为高效。PIML对特定的控制方程无偏见,因此在此我们考虑以下非线性ODE/PDE:
其中,u是表示模型,θ为其可学习参数。由于u是连续且可微的,因此可以通过自动微分计算源项和边界项f和b,表示为Fτ [u]和Bτ [u]【1】。PIML训练的目标是找到最优的可学习参数,以最小化逼近解与真解的已知组成部分之间的累积误差,如控制方程、边界条件或数据残差。该框架还可以通过为每个逼近解叠加约束,轻松扩展到ODE/PDE系统【19】。
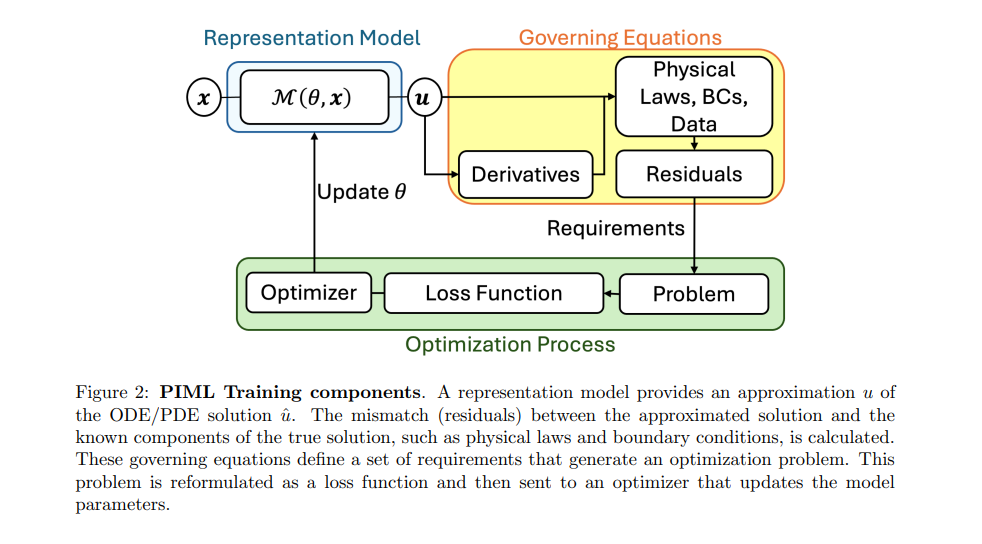
一般来说,当方程参数τ已知且边界条件已规定时,称为正问题,此时不需要域内的观测数据【1, 27】。相反,当ODE/PDE系统中的τ、边界条件或隐藏场等部分信息未知时,称为逆问题,目标是从现有数据或观测中同时推断未知信息和解【19】。整个PIML框架的示意图如图2所示。
PIML的算法发展
根据第2节概述的PIML框架,可以确定其三个关键组成部分:(1) 一个用于逼近解的表示模型,(2) 控制方程(例如ODE或PDE),以及(3) 一个优化过程,通过最小化多目标损失函数以找到最优的可学习参数(见图2)。当前研究通过针对这三方面的多种方法显著提升了PIML的基础性能,即对表示模型的改进、控制方程处理的进步,以及优化过程的改善。
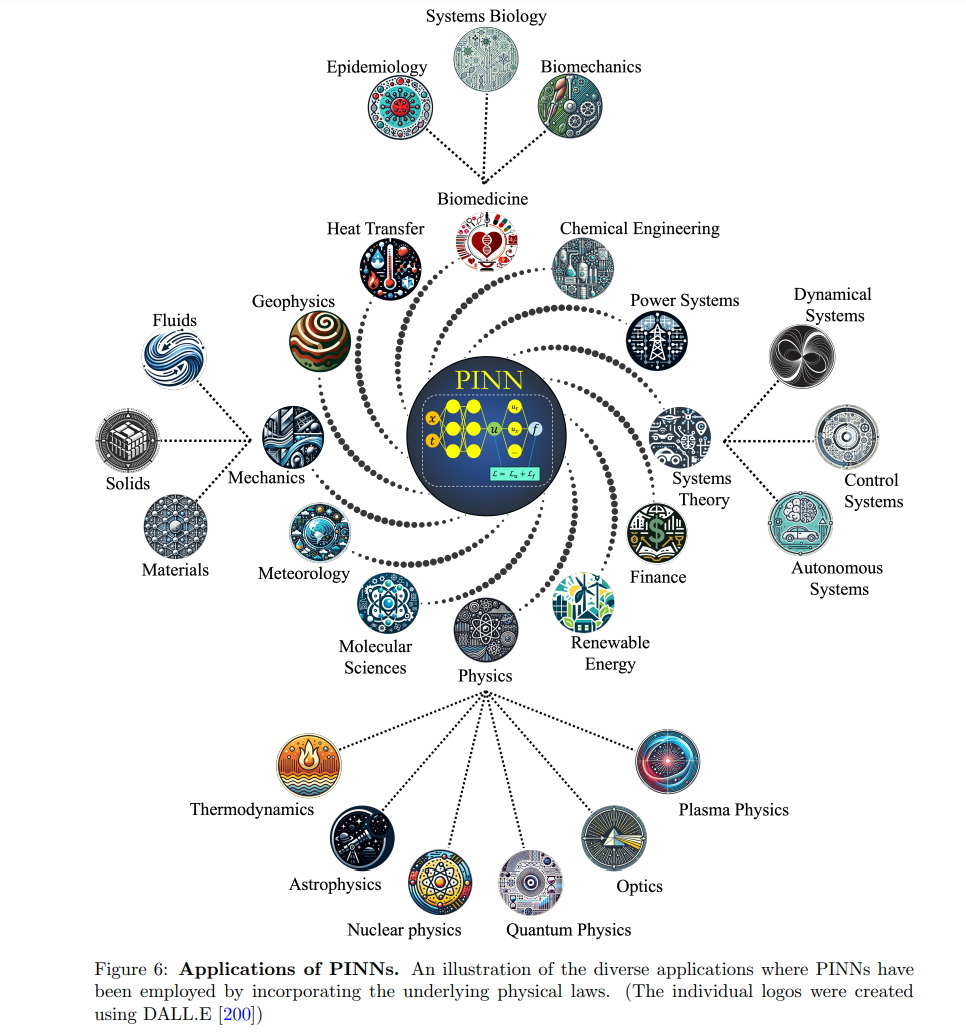
PIML的应用
大量研究表明,PIML在广泛的领域中取得了成功。本文对PIML在生物医学、力学、地球物理学、动力系统、控制与自主性、传热学、物理学、化学工程及其他相关领域的应用进行了精选而全面的回顾。