基于几何图学习的物理系统建模：从动态系统到复杂系统

导语

在当前基础科学研究中，绝大多数任务本质上可以归结为对不同物理系统的描述和建模。对蛋白质的结构预测让我们了解蛋白质的功能，分子动力学模拟让我们更好地了解化学反应的机理，对于系统结合能的预测让我们筛选更好的催化剂。随着近年来深度学习模型，特别是图神经网络模型的发展，越来越多的模型开始应用于从亚原子到大分子等一系列不同尺度物理系统的建模，取得令人瞩目的成果。在集智俱乐部「几何深度学习」读书会，阿里巴巴达摩院资深技术专家荣钰博士针对复杂物理系统和长时间动态系统，介绍了基于几何图学习（geometric graph learning）对这两类系统进行建模的最新工作以及相关应用，并对未来AI for Science相关领域进行展望。******

研究领域：图神经网络，几何图学习，AI for Science，复杂系统建模，动态系统建模**********

荣钰 | 讲者

董弘禹** | 整理**

荣钰、余孟君**** | 审校****

目录

1. 背景知识：物理建模系统的重要性

2. 基础概念回顾

3. 针对动态系统的建模

4. 针对复杂系统的建模

5. 未来展望

---

1. 背景知识：物理系统建模

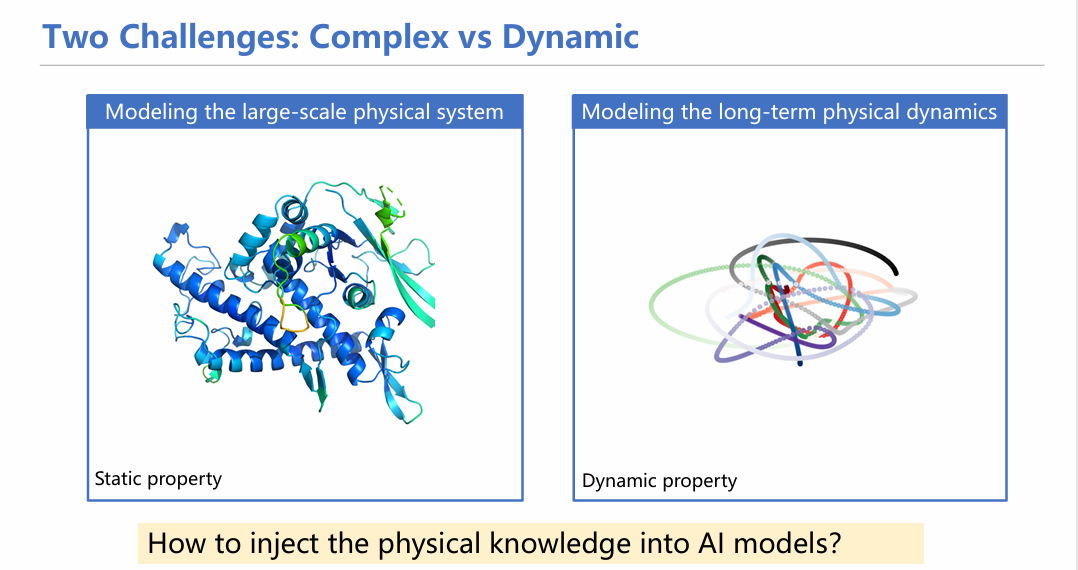
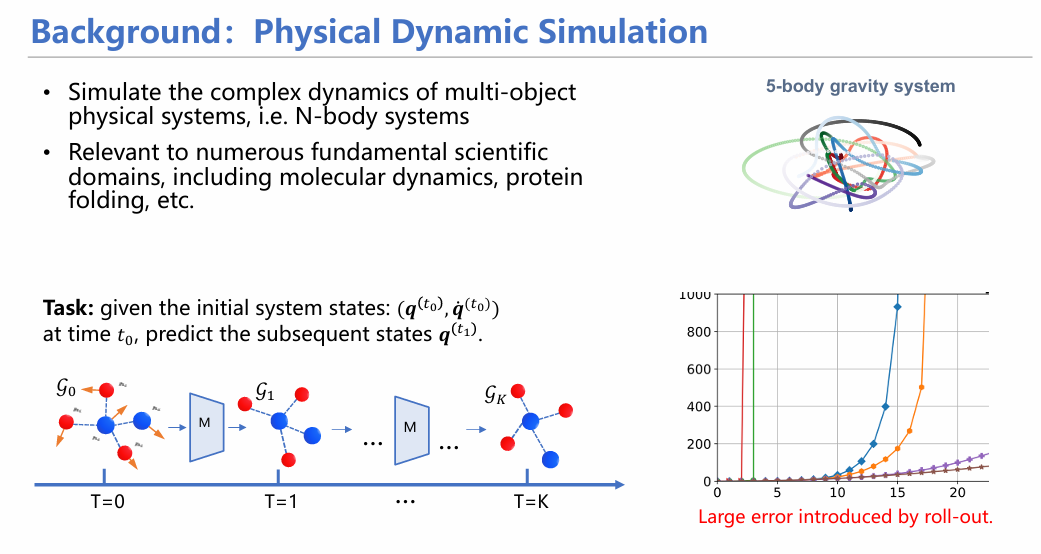
我们的世界中有很多物质，从微小的粒子到宏大的星系，其中蕴含着很多科学问题有待探索。近年来，AI4Science领域变得十分火热，不论是用人工智能模型对气体分子的扩散特性进行研究，抑或是研究分子对接问题，其本质是如何建模真实世界的物理系统。

我们可以把常见的挑战分为两类：对复杂静态系统的建模和长时间动态系统的模拟。静态复杂系统一个明显例子是对蛋白质结构进行建模，代表性的模型有AlphaFold，RoseTTAFold等等；动态系统则是研究某种分子/粒子的轨迹，或者对其动态特性进行研究，如分子动力学模拟。当然，这个划分只是为了方便研究，在真实场景下是二者皆有的，比如对蛋白动态对接的过程进行研究，这既要对蛋白结构进行建模（静态），也要对分子对接过程进行建模（动态），二者往往混合出现。

在没有人工智能方法的时代，物理学家、数学家们怎么做研究呢？他们的建模往往是借助数学工具去描述物理学的常识，例如如果一个粒子在经典力学条件下运动，那么就应该满足牛顿第二定律。随着大数据时代的到来和AI方法的广泛使用，科学家们开始从一大堆实验数据中尝试“拟合”满足要求的物理规律。然而，这种使用深度神经网络（Deep Neural Network， DNN）的方式很多时候是不足的，它并不能每次都拟合好所有函数。因此，如果将之前科学家们花费漫长时间研究得到的物理学先验知识“注入”到模型中，模型的效果应该会提升很快。在当前这个领域，大家都在研究如何将先验知识更好地嵌入到模型中，进而帮助建模基本物理问题。

2. 基础概念回顾

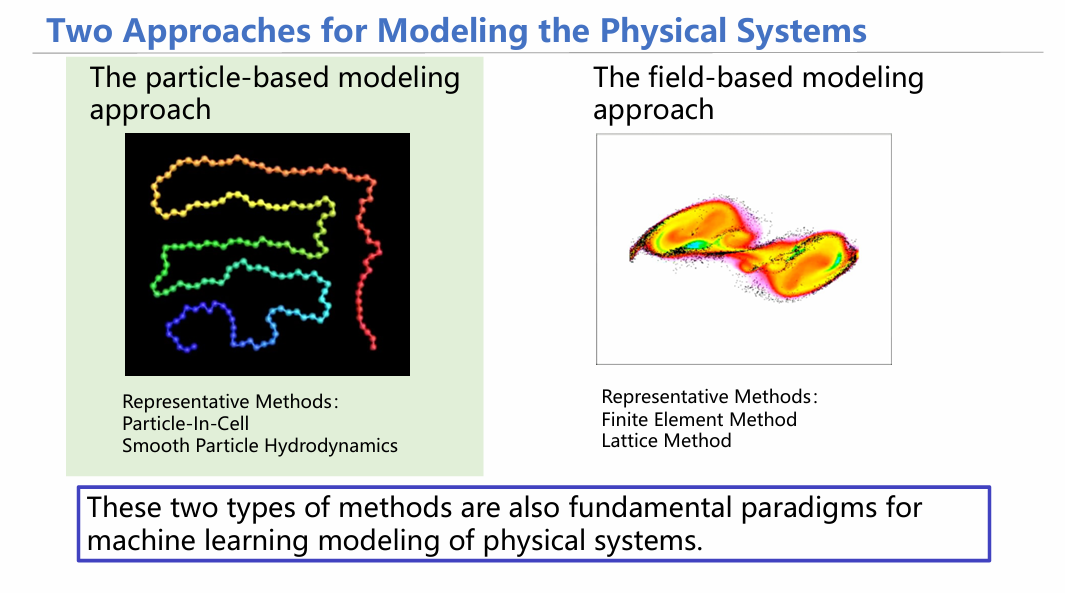
在介绍具体工作之前，我们一起回顾一下基础的背景知识，以便于后文的理解。首先，物理学家们通常采用两种办法对物理系统进行建模：基于粒子的建模方法，基于场的建模方法。基于粒子建模的核心是将物理过程看成由一堆具有特定属性的粒子交互运动的结果，通过研究粒子和粒子的交互来建模。而基于场建模的核心则是将物理过程看成空间中每个位置的特定特征变化，通过建模空间中这一连续的变化来研究物理系统。 在今天的讲解中，我们将主要着重于前者——基于粒子的建模方法。

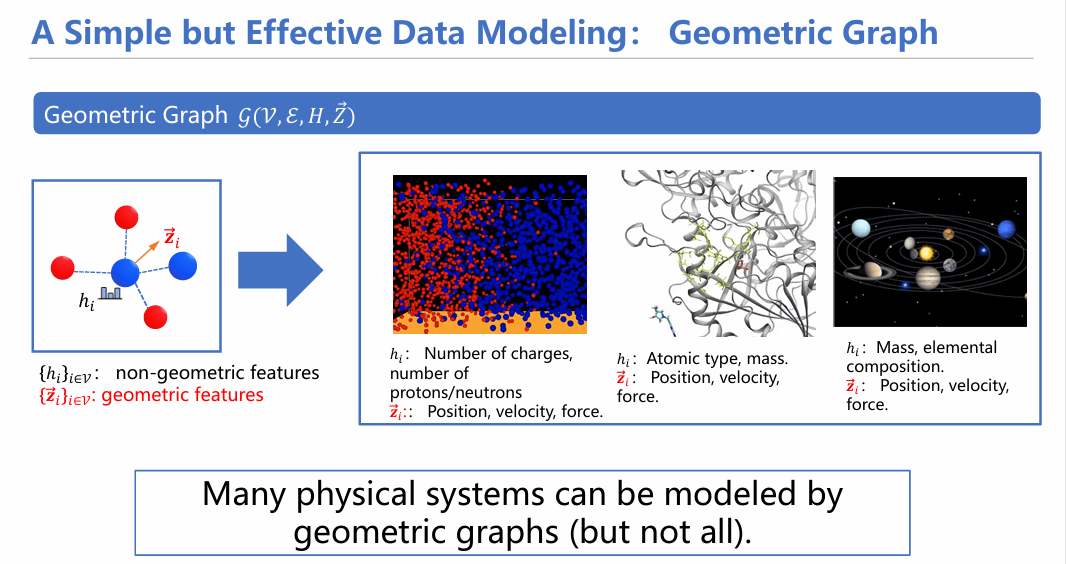
在基于粒子的建模中，对于数据的描述往往采用几何图的形式。什么是几何图？简言之就是在传统图的基础上，增加一些几何特征（如空间三维坐标表示、受力情况、速度等参量）。由于引入了很多粒子的附加信息，因此相比于传统的图，其内容和特征表示更丰富，更便于对物理系统进行建模。

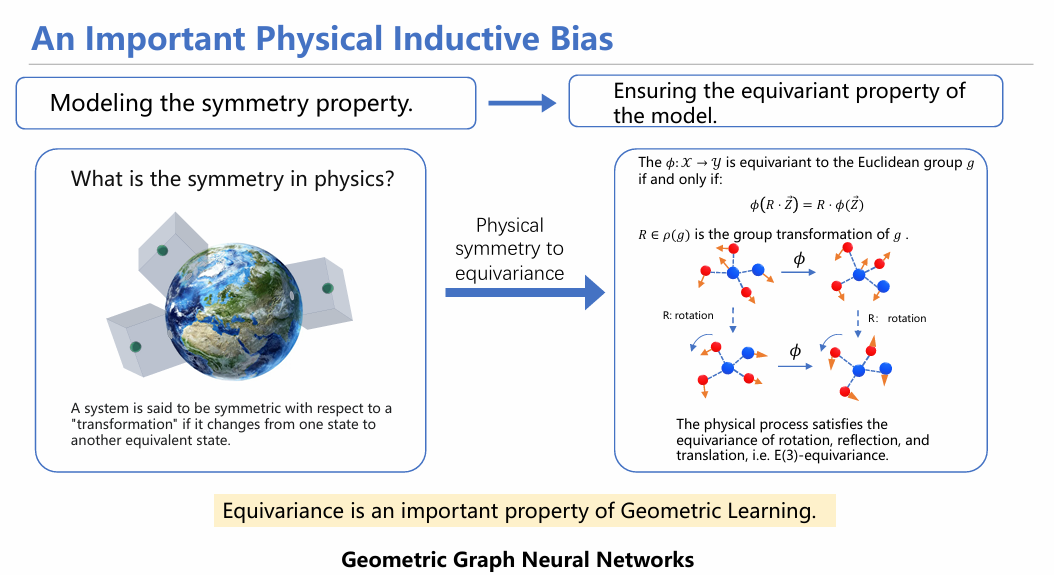
讲到这里，我们就要引入一个概念，叫偏置假设（Inductive Bias）。这个术语用来形容一些系统中最基本的性质，最基本的先验知识。在几何图中，这种假设被称为“等变性”。

**等变性这个概念来源于物理中的对称性。**如果我在一个物体上施加一个变换，变换前后物体性质保持不变，则称这个物体对这个变换保持对称。推广来看，如果对于一群粒子、一个变换函数和一个旋转变换R，先对粒子做旋转变换，后做变换，与将这两个操作反过来实现的效果是一样的话，则可称为具有等变性。

我们处理几何图，一般采用几何图神经网络。它与传统图神经网络的最核心区别就是保持了等变性。我们可以从下面这张图所展示的消息传递方式对比它与传统网络的区别。传统网络仅有黑色（1、3行）所示的传递方式；在蓝色部分增加了几何信息的生成和传递。可以看到，通过并行进行消息生成与传递，几何图神经网络能够将几何信息充分融入，进而保持等变性。

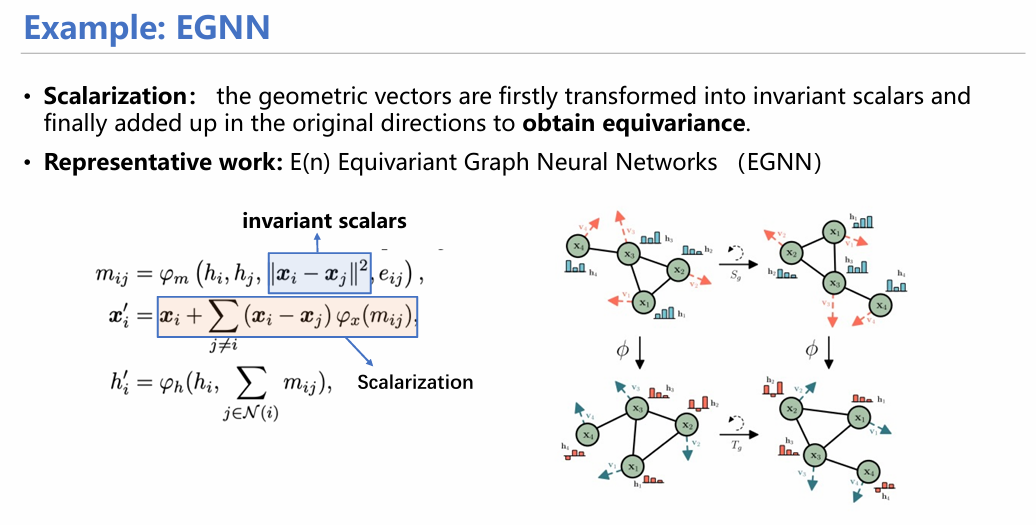
谈及等变神经网络，就不得不提到这篇EGNN[1]工作，它用一种很简单的标量化操作——首先采用计算欧氏距离的形式得到一个标量数值，进行常规消息传递，当更新几何信息时（这里具体化为坐标x）用xi- xj的形式产生一个带方向的向量，进行加权平均求和更新坐标。这样的方式虽然很简单，但是却很有用，后面基于EGNN的工作也都是从这个基础上进行改进。因此，这篇文章是当之无愧的经典和鼻祖，值得我们仔细研读。有关更多的等变网络构造的方式和相关的应用也可以参阅我们最近发布的综述[6]。

3. 针对动态系统的建模

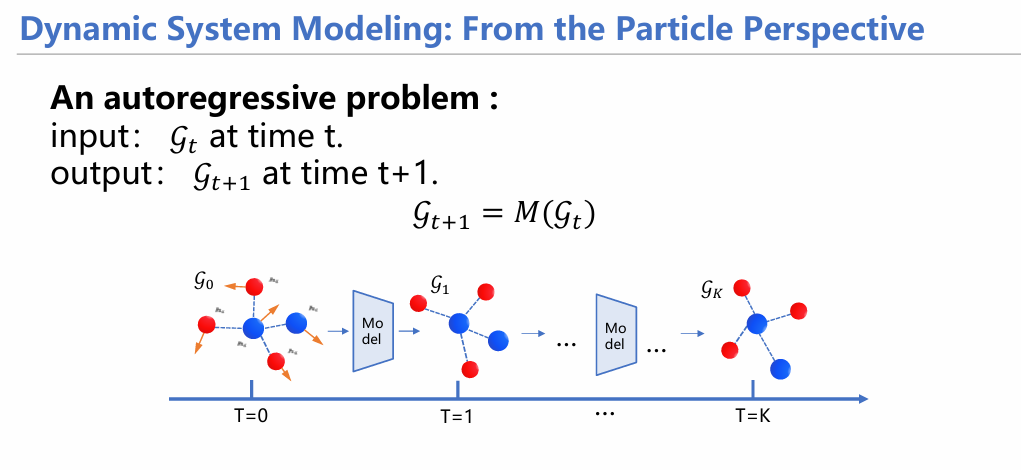
我们这里所谈到的动态系统建模，实际上可以归纳为一个自回归问题，输入t时刻的一种粒子状态图，产生下一时刻的粒子图。

然而，这种预测是有些许问题的，需要额外知识的嵌入。在接下来的讲解中，我们将阐述建模动态系统时的一些问题，针对这些问题，我们融入了哪些先验偏置假设从而改进预测效果。 下面主要介绍三个工作。

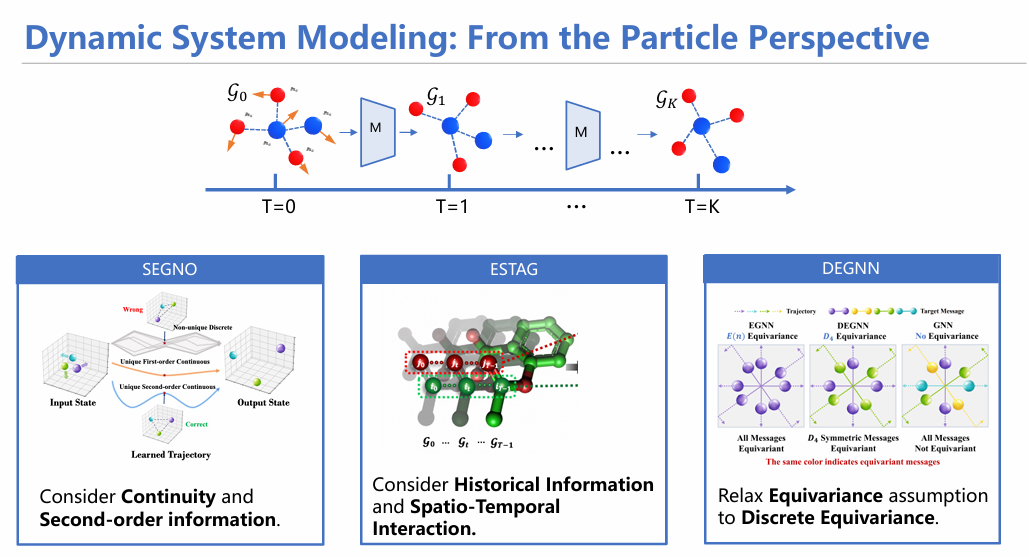
3.1 SEGNO: Second-order Equivariant Graph Neural Ordinary Differential Equation[2]

在建模动态系统时，物理学家能够运用经典物理规律（如牛顿第二定律）对每个粒子的运动进行模拟。然而，随着粒子数的增加，计算复杂性急剧上升，这对计算资源的要求更为苛刻。此外，随着时间和迭代次数的增加，每一步的误差会逐渐累积，直至系统崩溃。这两点困难使得长时程预测任务难度骤然上升。

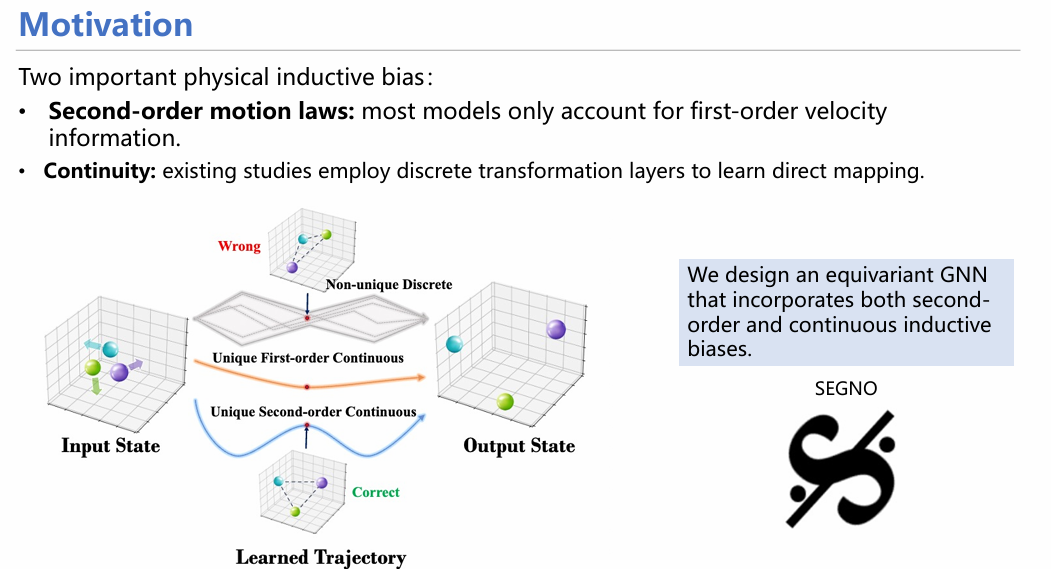
经过文献调研与细致分析，我们发现有两点先验知识之前没有涉及：1）许多模型仅关注从前一时刻的位置预测后一时刻的位置（仅有一阶信息）。然而在物理学领域，逻辑应该是：分析受力-得到加速度-求解速度-求解位移，应该增加对加速度的预测和考量（二阶信息）；2）现有数据极其稀疏，仅有这一时刻和下一时刻的离散化数据，至于中间经历了什么无法知晓。针对这两点局限，我们设计了SEGNO框架，将两种先验假设融入模型中。

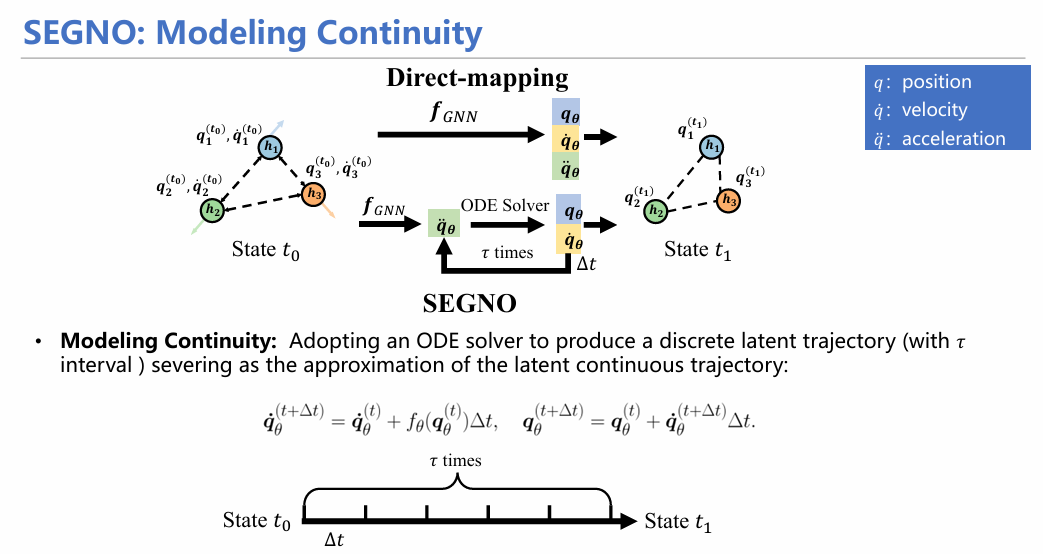
具体而言，模型首先采用一个MLP网络对加速度进行建模，然后将加速度这个参量融入几何图神经网络中进行消息传递，随后采用常微分方程（ODE）对速度、位移等参量进行求解；此外，通过欧拉方程的方式，模型能够很好地求出t0-t1时间段内以Δt 为间隔的粒子位置和速度，从而能够在离散的过程中插值未观测量。

在计算损失时，模型仅计算t1时刻由模型预测出的粒子位置和真实位置之间的距离。

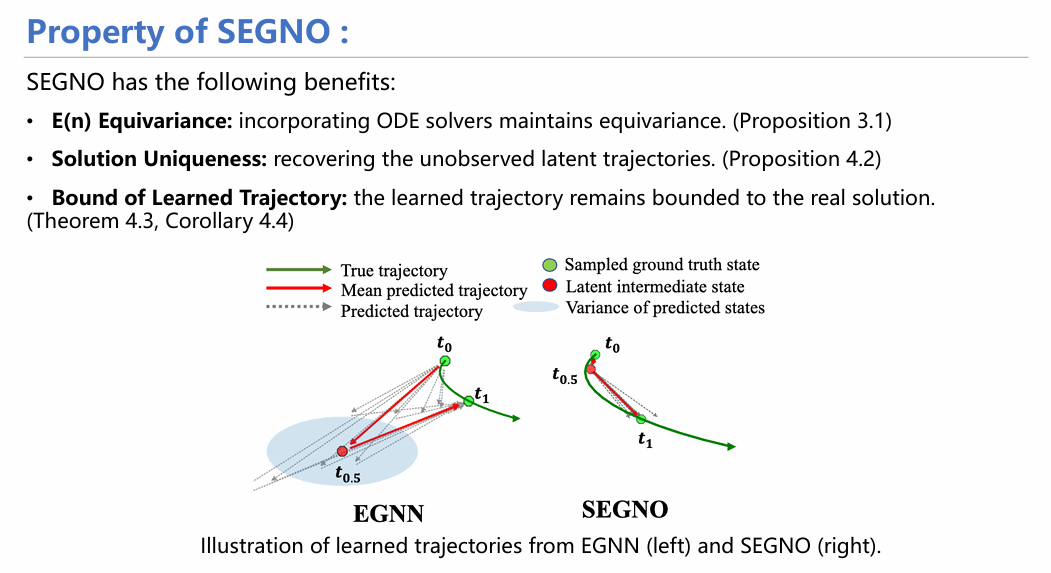
在理论证明上，SEGNO能够证实模型具有等变性，解唯一性；且通过下图实验可看出与传统的EGNN相比，SEGNO在可以保证在t0-t1过程中的路径唯一性，同时这一路径也可以准确预测t0.5这个中间量。

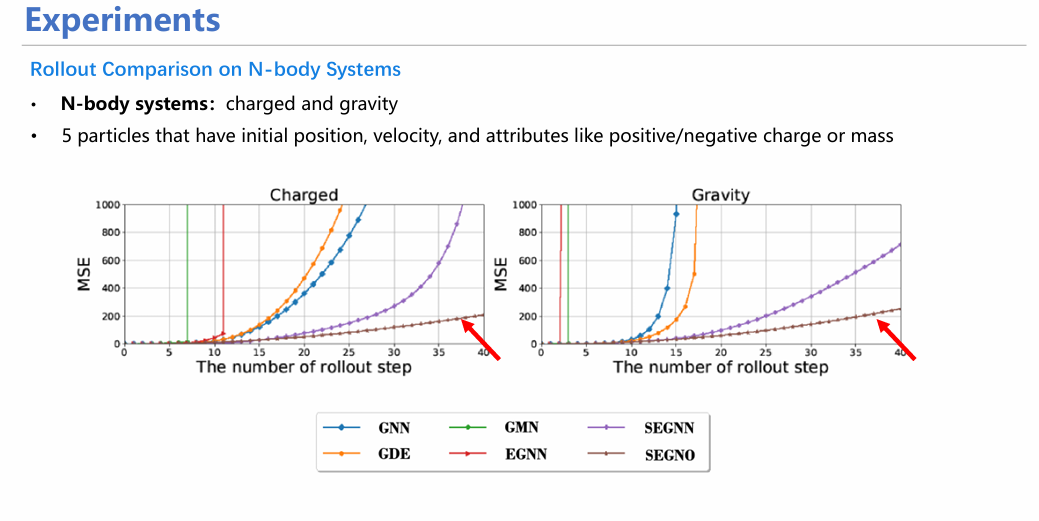
从具体实验来看，SEGNO不仅能在定量实验（如方向预测实验）中取得较高指标，均方误差（MSE）较小；同时也十分稳定，具体表现在随着迭代次数增加，SEGNO的误差增长曲线较其他模型更为平缓，证明其每一步的误差均控制在较小范围。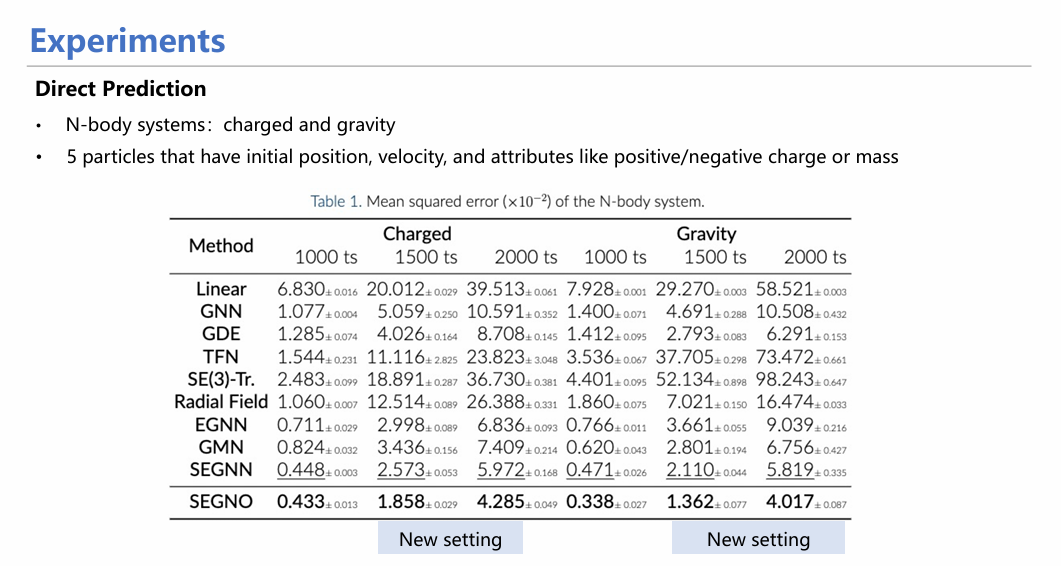

在许多下游任务，如分子动力学模拟和人姿态估计预测上，模型也能超过现有方法，实现更好的效果。

总结而言，SEGNO模型通过加入两种先验假设：二阶参量和连续性插值预测，从而更好地建模长程问题。需要注意的是，模型能够应用于各种backbone模型上，泛化性很强。

3.2 ESTAG：Equivariant Spatio-Temporal Attentive Graph Networks to Simulate Physical Dynamics[3]

在蛋白质建模中，研究者们通常关注于蛋白质和小分子的结构，以及它们如何完成诸如对接这样的动态过程。但实际上，二者都在同一溶剂中进行反应，溶剂分子是不可忽视的一种角色。溶剂分子通过与配体、受体进行互作，有可能影响对接过程。

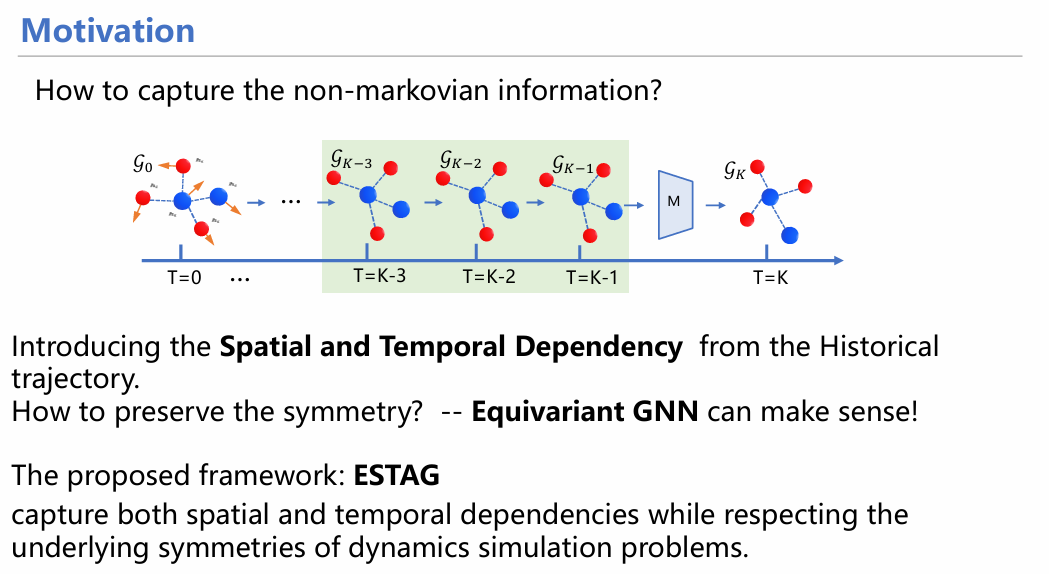
如果采用数学语言精炼化描述上述情况，我们可以认为，之前所述的理想模型满足马尔科夫链结构——任意t时刻的分子状态图只和其前一时刻t-1状态图有关。然而，实际情况不满足马尔科夫性质，t时刻的图和t-1、t-2乃至t-3时刻状态图有关，此外，不同位置的粒子之间也互有作用。总之，要考虑时空依赖性进而对分子状态进行精确估计。

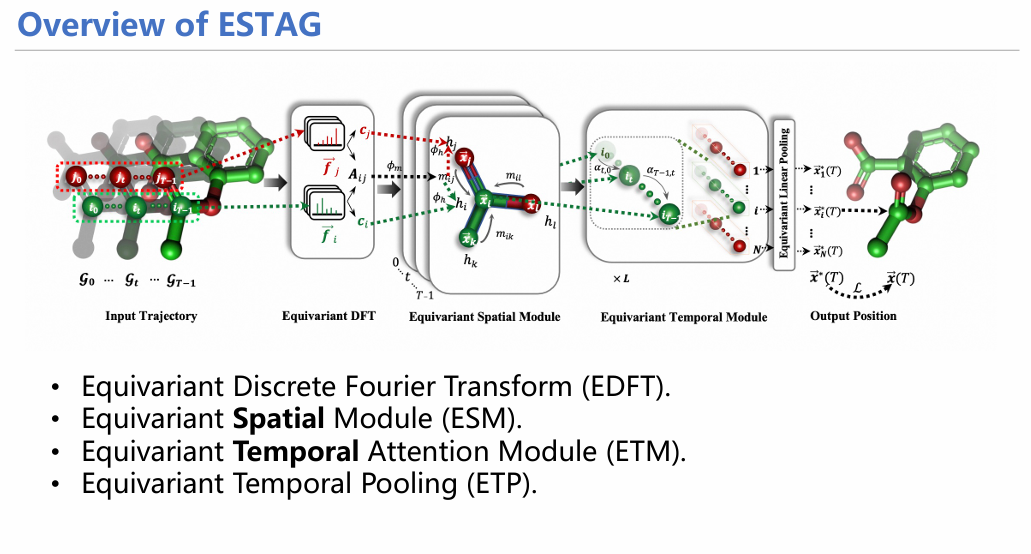
鉴于此，我们开发了一种融合时空信息的等变图神经网络框架ESTAG，用于进行粒子模拟。此框架分为四个部分：

1. EDFT：使用离散傅里叶变换将时域信息转化成频域信息；
2. ESM：融合空间信息的消息传递模块；
3. ETM：融合时间信息和注意力机制的消息传递模块；4. ETP：Pooling模块，将频域转化回时域。

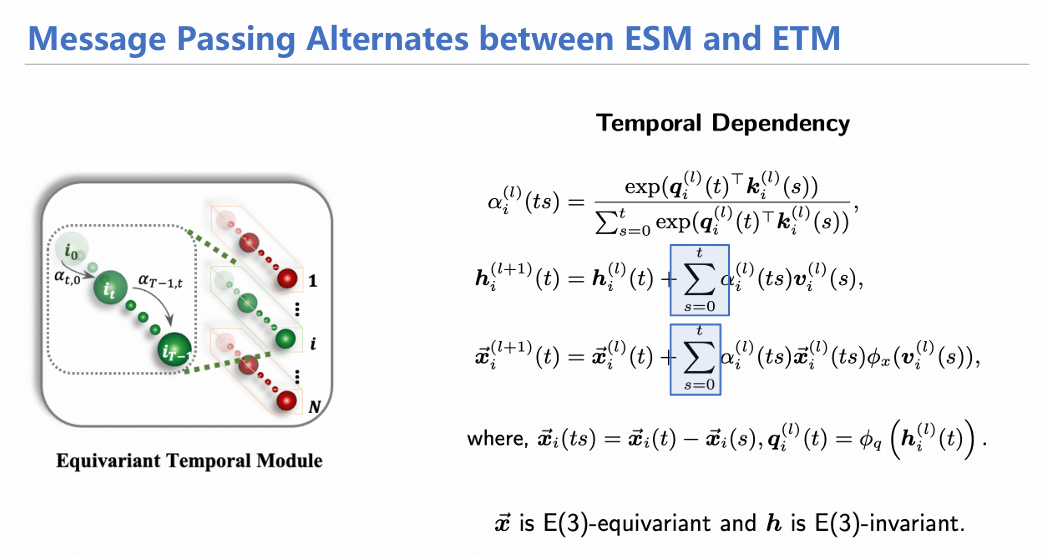
下面两张图大体概括了时空传递机制，其实和EGNN的方式大体相当，只不过在时间信息传递时采用了注意力机制，对从0时刻开始的状态（坐标，速度）进行加权求和，随后生成信息用于下一次传递。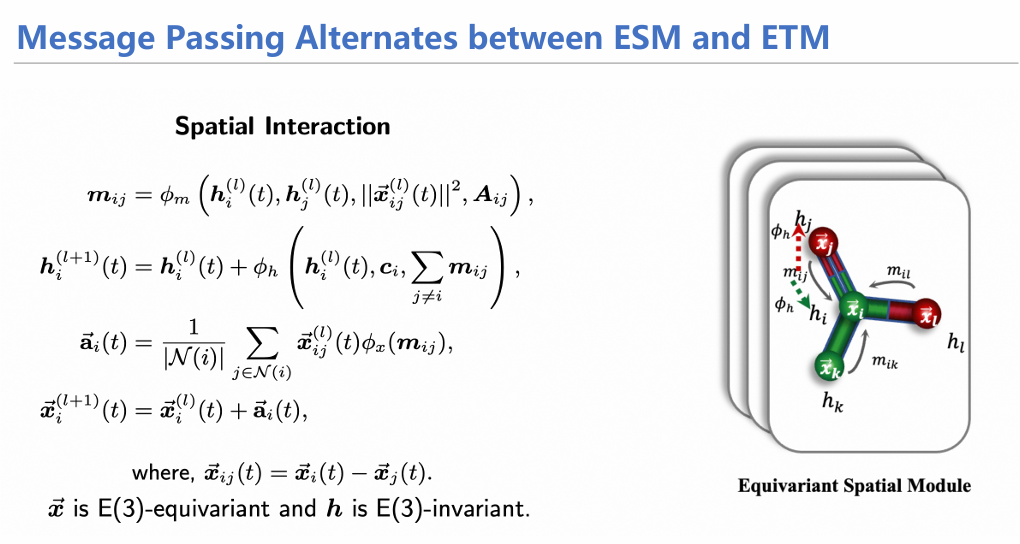

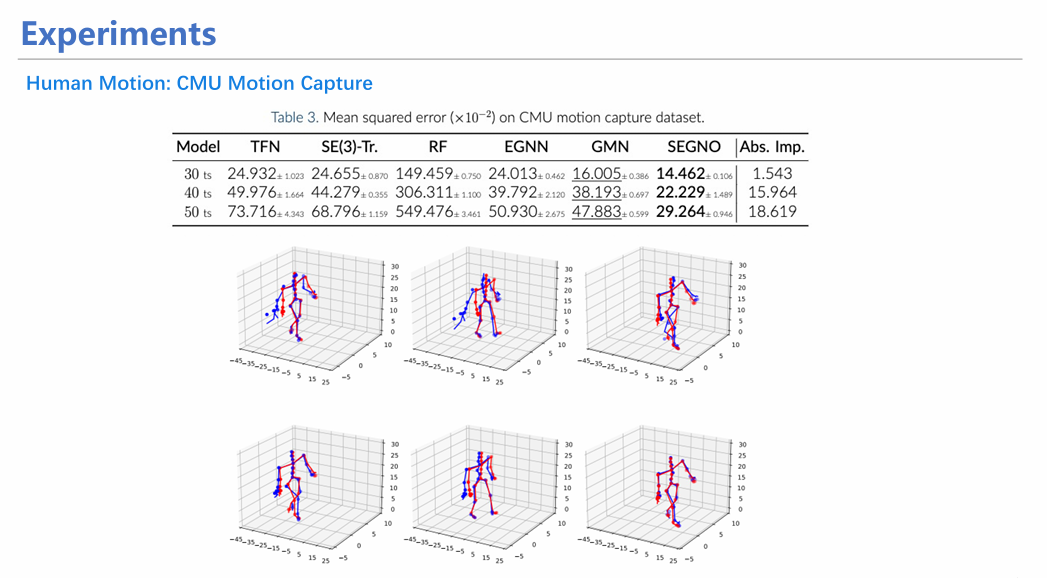
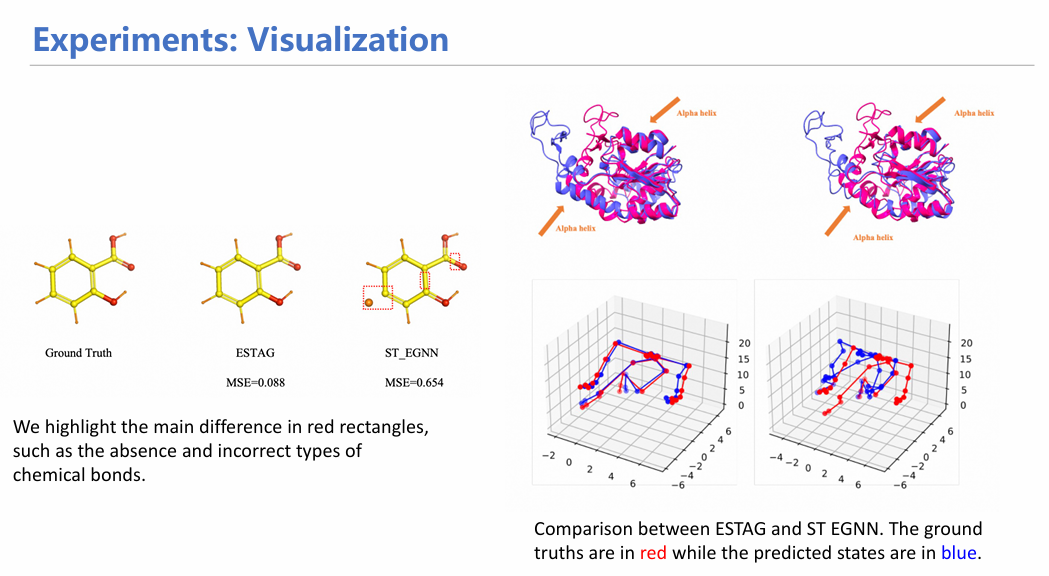
通过在分子模拟数据集MD17上的实验，我们证实了融合时空信息确实能够让模拟性能提升一个数量级，从更宏观的蛋白数据集上也收获到了类似的效果。可视化实验也证明了ESTAG能够在预测过程中保留EGNN丢失的化学键，并能更精确地生成蛋白质alpha折叠和人体姿态数据。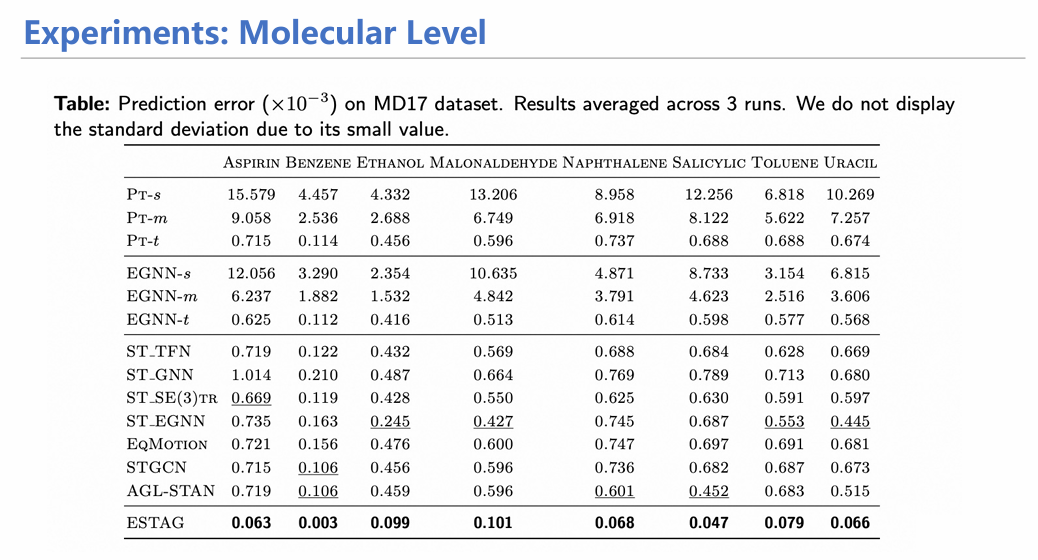

总结而言，ESTAG模型融合时空信息进行消息传递，进而提高粒子模拟性能。该论文也中稿了NeurIPS 2023年的poster。

3.3 DEGNN: Discrete Equivariant Graph Neural Network[4]

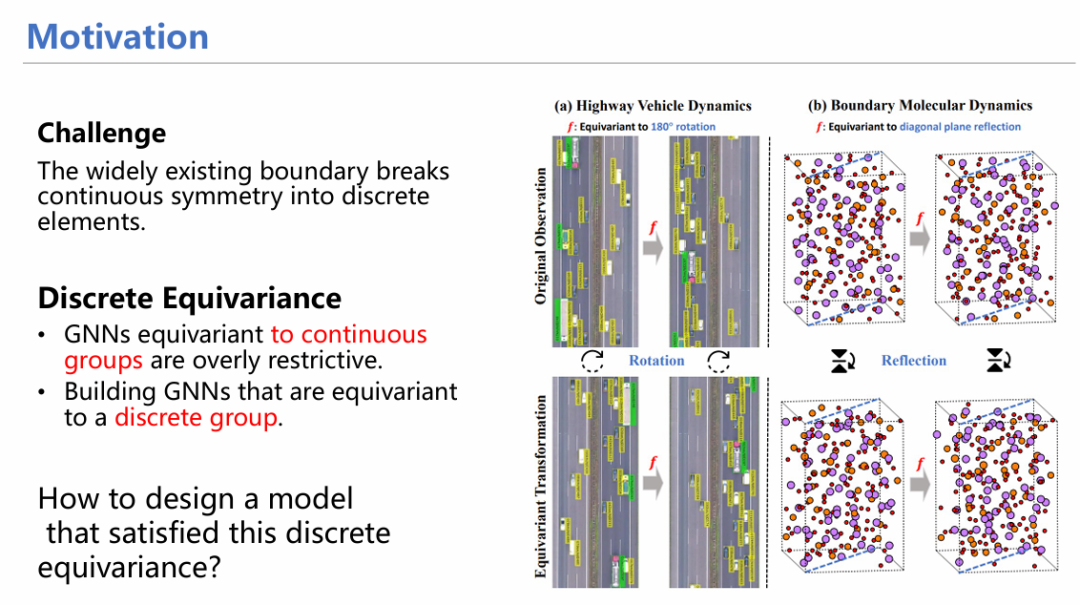
几何深度学习的等变性约束已经广为人知，并应用到各个领域。然而，对所有系统都加以等变性约束是否太过严格？例如，高速公路上的汽车永远不会跑出路，因此它的等变性只体现在旋转180度后有效。因此，有必要探究在不同的离散等变群上适当放松等变性约束，是否更为合理？

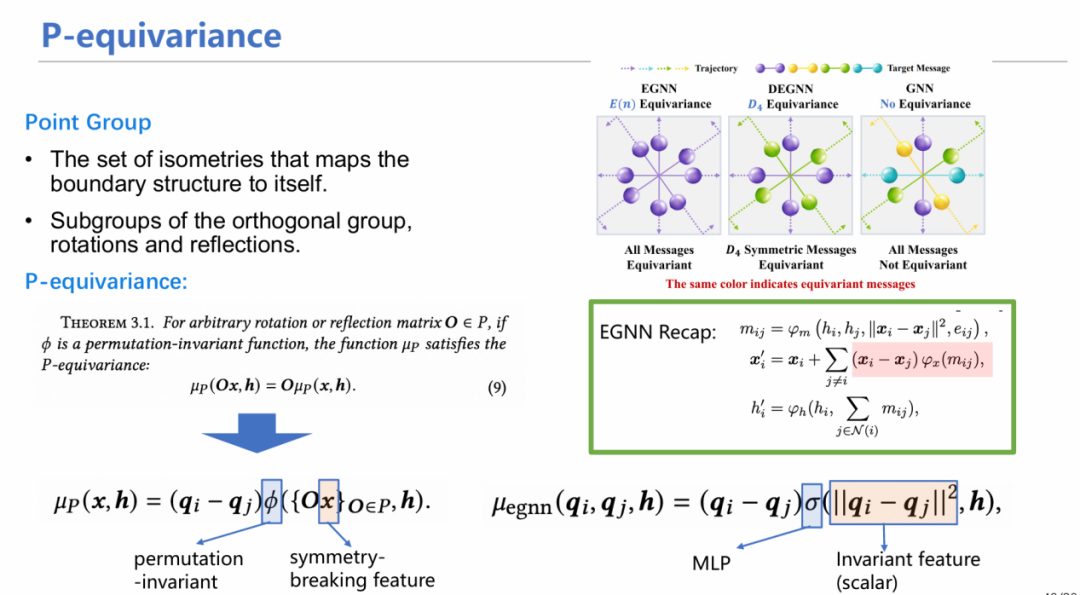
借鉴晶体里面的概念，我们首先定义点群（point group）。点群是传统等变性的放松约束形式，它由一群离散操作组成，这些操作使粒子保持离散等变性。举个简单的例子，D4等变群[7]包含了将粒子旋转90、180、270、360度这四种等变性操作。我们有了离散等变群之后，下一步的关键就是如何构造函数，使得模型能够实现离散等变操作。 下面是一个构造方式μp，它既能保持排列不变性（输入数据顺序不同其输出结果相同），又能保持离散等变性。对比和EGNN的区别，可发现其核心是将EGNN模型σ中从向量转化为标量这个约束进行了放松，将约束转移到φ上，只要φ满足排列不变性，那么对于任意给定的点群，下面的构造都可以满足离散等变性。所以x的对称性破缺特征（symmetry-breaking feature）其实就是表明x不用是标量了，而可以是一堆向量也满足条件。因此，μp是EGNN的一般性表示。

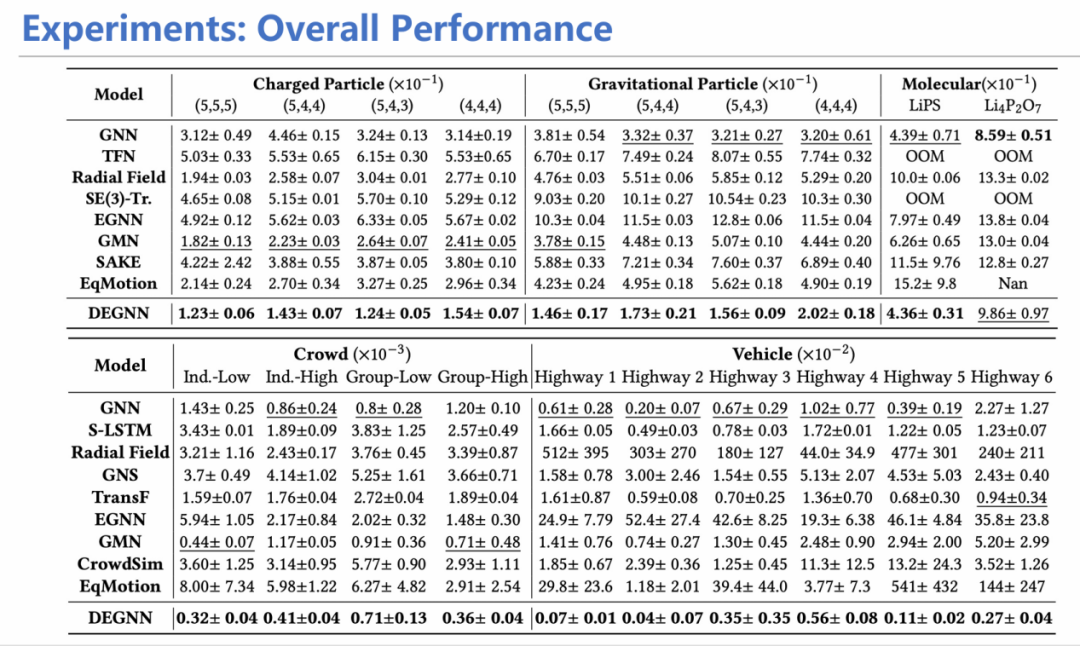
我们采用这样的构造方式搭建模型，并进行了从宏观到微观的不同物理系统（如高速公路、分子动力学）的实验。结果证明，模型在各个领域的实验均表现优异，从而证实本研究开头提到的假设：等变性约束往往太过严格，适当放松约束也是不错的选择，为未来模型设计和研究提供了参考。

这篇文章同时也中稿KDD 2024，用构造函数的方式向研究者们展示放松等变性约束也不失为一种有效办法。

4. 针对复杂系统的建模

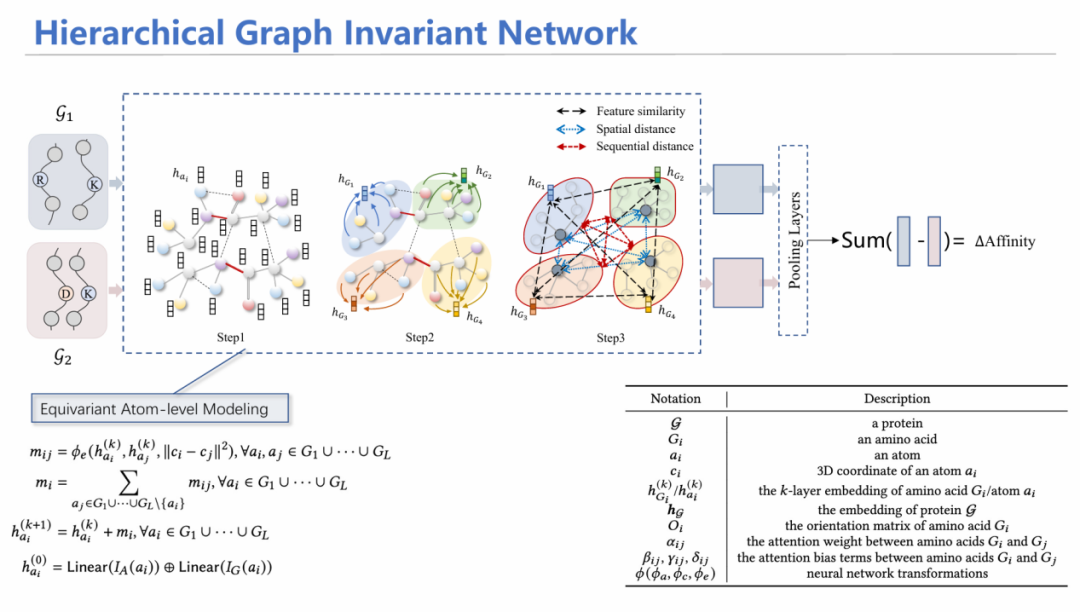
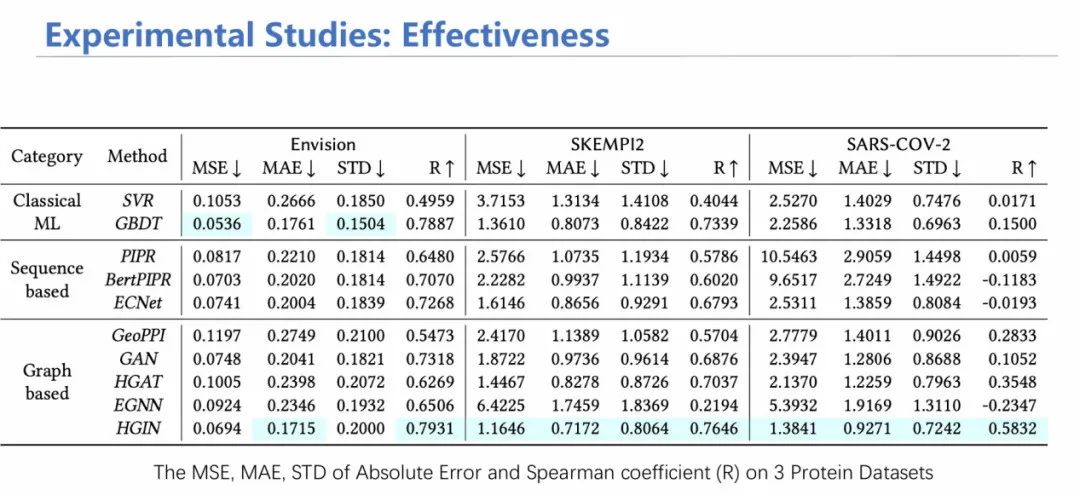
以HGIN: Geometric Graph Learning for Protein Mutation Effect Prediction[5]为例，我们展示等变图神经网络在复杂系统建模上的应用。 在蛋白质建模任务中，有一种任务称之为定向进化。其本质是通过突变，探究蛋白亲和力的变化，如果亲和力增加，则保留这个突变，在该突变基础上继续突变，从而迭代改进蛋白质。

已有工作采用序列输入的方式，用循环神经网络/大语言模型进行建模；此外还有通过卷积核卷积蛋白三维结构对特征进行汇总。存在两个挑战：1）未考虑不同层次的特征：由于是单氨基酸突变，如果从氨基酸序列层面来看，序列变化十分微小，可能在模型学习过程中无法学习出差异信息；然而从原子层面上看，突变一个氨基酸产生的影响比较大——因此要融合不同层次的信息。2）在亲和力预测时，要满足等变性。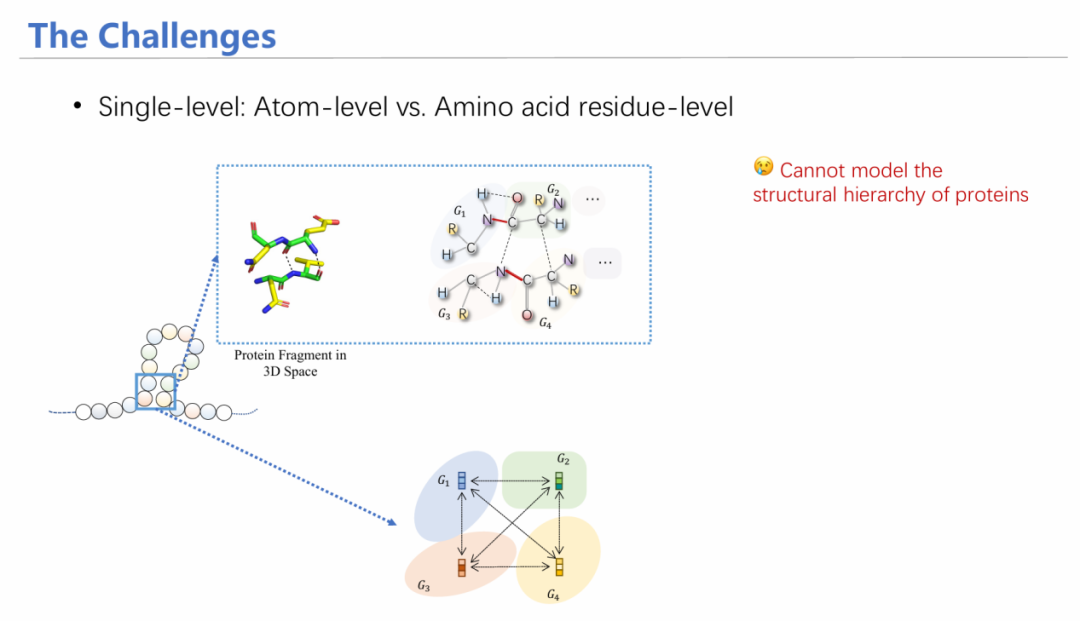

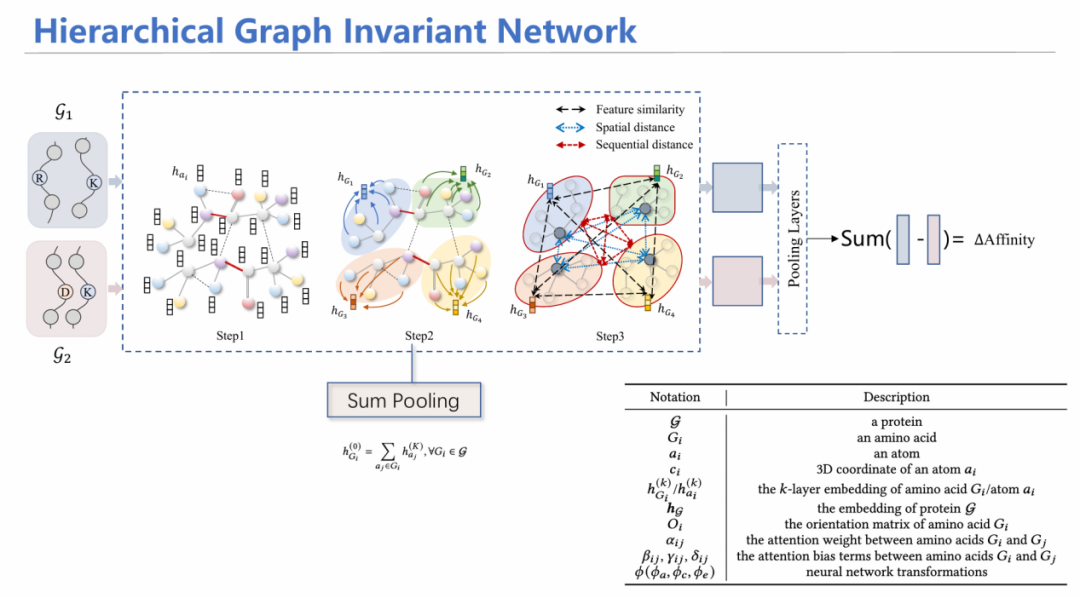
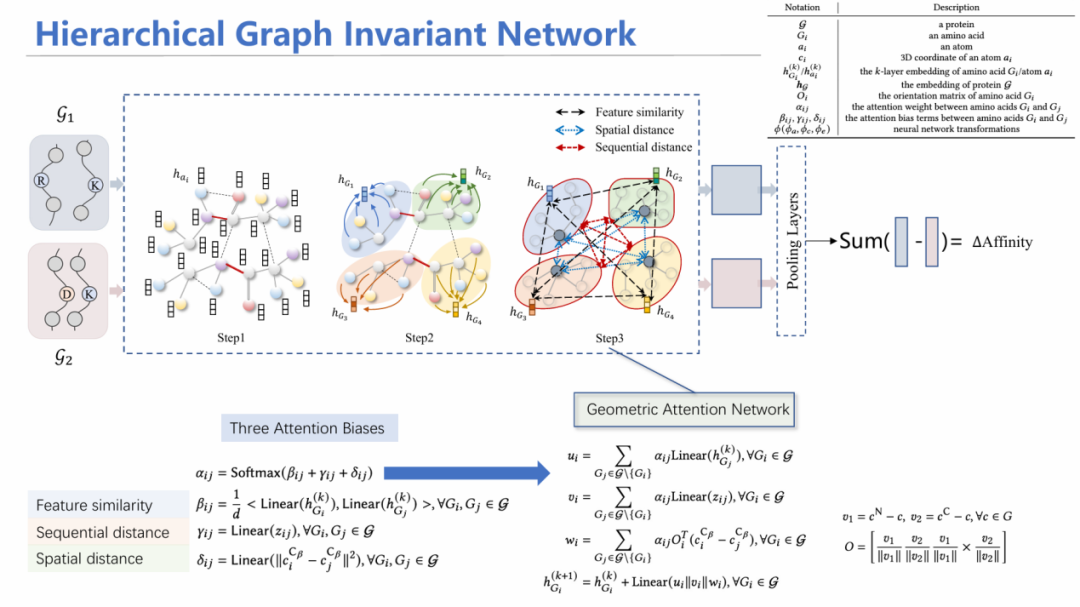
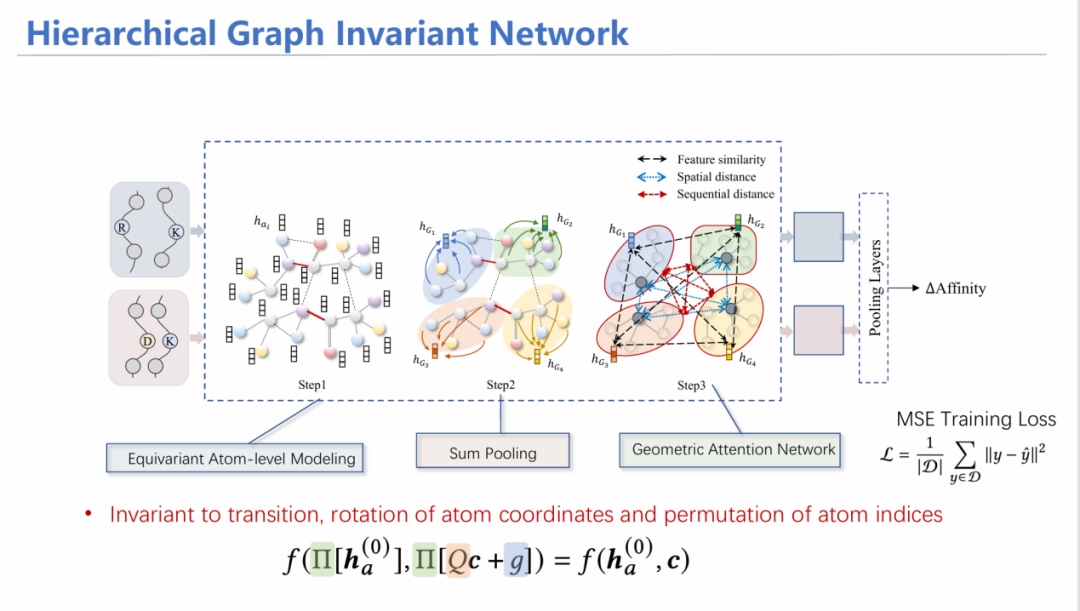
为此，我们设计了HGIN——层次等变图神经网络模型。模型同时输入野生型和突变型结构，首先从原子层面进行消息聚合，随后通过池化（Pooling）方式将其汇总到每个氨基酸的特征；在氨基酸层面，考虑氨基酸之间的特征相似性、空间上是否相近、在序列上的位置等多角度信息进行注意力机制加权平均求和，最后预测出两个潜在表示，加上MLP层预测亲和力变化情况，同原来已知的标签进行监督学习。

通过一系列数学证明，能够证明这个模型也满足几何等变性和排列不变性。

通过在单链蛋白数据集、多链蛋白数据集、病毒数据集上进行主要实验，可证明通过融合层次化信息，模型的性能得到有效的提高。

5. 未来展望

科学研究的范式可分为两类：一类是开普勒的数据驱动型——给定大批数据，通过AI模型学习底层规律；另一类是牛顿的模型驱动型——从第一性原理开始推导，建立理论框架。在当今的研究中，我们是否能将这两种范式进行结合呢？能否通过注入物理先验知识，在有限的数据下训练出一个“足够聪明”的大模型呢？值得大家思考。

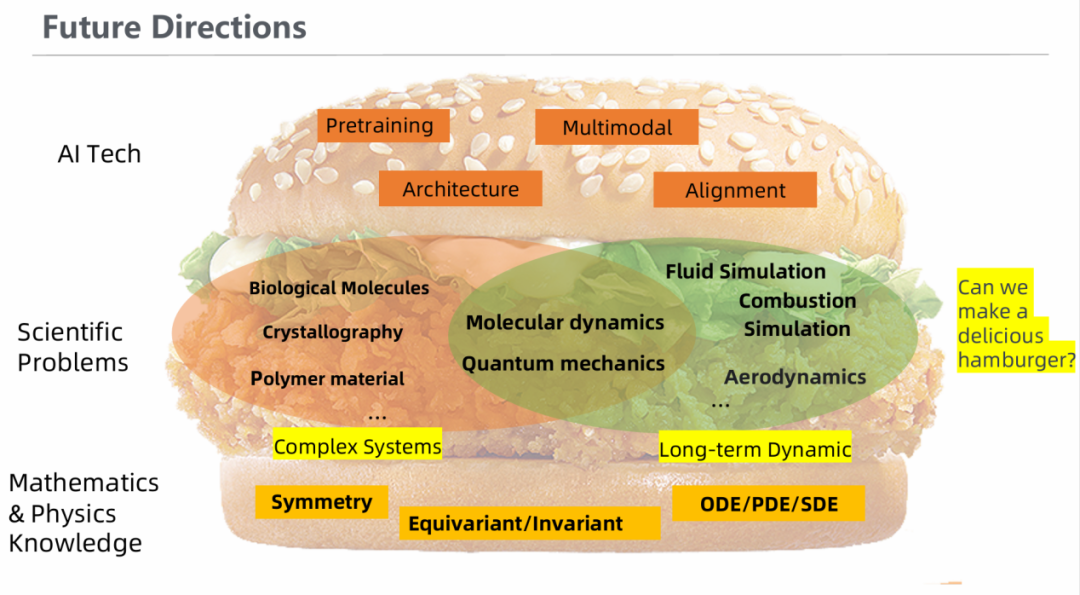
AI for Science领域的大模型应该怎样做？在我看来，科学问题涵盖的领域非常广泛，从生物到物理。其问题的尺度和复杂性也各有不同，大到天体，小到微粒。在过去数百年的研究中，科学家们已经积攒了非常丰富的多尺度数据，那么我们能否通过融入一定的先验知识，研发出多模态、多尺度大模型，从而打通各个领域，助力科学发现呢? 如果能实现，那么我们就可能通过分子动力学模拟去预测蛋白结构，通过蛋白质结构预测催化系统的结合能。 我们有强大的算力和性能优异的算法，我们也有长久积累下来的物理学定律，如何用这两块面包，解决很多重要的科学问题（里面的鸡排），从而做好这个汉堡包，获得新的科学范式，是各位研究者们未来奋斗的目标。

展望未来，AI for Science的基础模型可以通过大语言模型外加知识库的形式进行发展，也可打造一批专业领域模型供大语言模型进行调用，这些可能都会在不远的将来实现，未来可期！

参考文献：[1] Satorras, Vıctor Garcia, Emiel Hoogeboom, and Max Welling. "E (n) equivariant graph neural networks." International conference on machine learning. PMLR, 2021[2] Liu, Yang, et al. "SEGNO: Generalizing Equivariant Graph Neural Networks with Physical Inductive Biases." The Twelfth International Conference on Learning Representations, 2024, https://openreview.net/forum?id=3oTPsORaDH.[3] Wu, Liming, et al. "Equivariant Spatio-Temporal Attentive Graph Networks to Simulate Physical Dynamics." Thirty-seventh Conference on Neural Information Processing Systems, 2023, https://openreview.net/forum?id=35nFSbEBks.[4] Zheng, Zinan, et al. "Relaxing Continuous Constraints of Equivariant Graph Neural Networks for Physical Dynamics Learning." ArXiv, 2024, https://arxiv.org/abs/2406.16295.[5] Zhao, Kangfei, et al. "Geometric Graph Learning for Protein Mutation Effect Prediction." Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, ACM, 2023, pp. 3412–3422, https://doi.org/10.1145/3583780.3614893[6] Han, Jiaqi, et al. "A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications." arXiv, 2024, https://arxiv.org/abs/2403.00485.[7] Mondal, Arnab Kumar, et al. "Group Equivariant Deep Reinforcement Learning." arXiv preprint arXiv, 2020, https://arxiv.org/abs/2007.03437.