【AI+生物医学】耶鲁大学最新博士论文《图先验、最优传输和深度学习在生物医学发现中的应用》231页pdf

2022 年 4 月 29 日 专知

摘要

生物医学数据收集的最新进展允许收集大量数据集，测量数千到数百万个单细胞中的数千个特征。这些数据有可能以以前不可能的分辨率推进我们对生物机制的理解。然而，了解这种规模和类型数据的方法很少。尽管神经网络在监督学习问题上取得了巨大进步，但要使它们对更难表示监督的数据中的发现成为有用，还有很多工作要做。神经网络的灵活性和表现力有时会成为这些监督较少的领域障碍，从生物医学数据中提取知识就是这种情况。在生物数据中更常见的一种先验知识以几何约束的形式出现。

在本论文中，我们旨在利用这些几何知识来创建可扩展和可解释的模型来理解这些数据。将几何先验编码到神经网络和图模型中，使我们能够描述模型的解决方案，因为它们与图信号处理和最优传输领域相关。这些链接使我们能够理解和解释这种数据类型。我们将这项工作分为三个部分。第一个借用图信号处理的概念，通过约束和结构化架构来构建更具可解释性和性能的神经网络。第二个借鉴了最优传输理论，有效地进行异常检测和轨迹推断，并有理论保证。第三个研究如何比较基础流形上的分布，这可用于了解不同的扰动或条件之间的关系。为此，我们设计了一种基于联合细胞图上扩散的最佳传输的有效近似。总之，这些工作利用我们对数据几何的先前理解来创建更有用的数据模型。我们将这些方法应用于分子图、图像、单细胞测序和健康记录数据。

引言

数据分析领域在不断变化。有人问是否会有一天我们不再需要新算法，数据分析领域就像从现成的工具中挑选合适的工具并将其应用于一些新数据一样简单。答案当然是否定的，只要数据、计算机或问题不断变化，我们将始终需要新的算法和方法。

数据生成、处理和存储方面的进步为我们提供了前所未有的从这些数据中学习的能力。在某些领域，几何数据分析领域试图利用点之间的局部关系来理解数据。

随着廉价测序技术的出现，单细胞数据分析领域直到最近才成为可能，使我们能够同时测量单个细胞的许多特征。这导致来自底层连续流形的非常高维和嘈杂的数据集。这种对数据生成过程的假设是整个工作中的一个共同主题，我们将看到其他先验知识开始发挥作用，这些先验最好使用一种或另一种文献进行描述。

本论文从第 2 章中对图信号处理、深度学习和最优传输的概述开始。虽然这些领域是从不同的文献中发展而来的，但每个领域都试图理解从一些基础度量空间中采样的点或点的分布如何相互关联。在本论文中，我们融合了来自这些领域的想法，以深入了解生物医学数据，重点关注单细胞转录组数据以及其他图形和图像数据集。这些数据类型的共同点是它们要么在图数据集中具有点之间的一些内在关系，要么假设是从一些可以在本地表示的底层低维流形中采样的。

本论文分为三个部分，第一部分侧重于融合深度学习和图信号处理，通过借鉴图信号处理的思想来制作更具可解释性的深度学习组件，并借鉴深度学习的思想来制作从图信号开发性能更高的固有可解释模型加工。第二部分融合了深度学习和最优传输，以创建具有可解释属性的深度学习模型。最后，在第三部分中，我们将其完整循环，将最优传输和图形信号处理相结合，以一种基于嵌入的快速方法来优化从底层流形采样的点的传输。这种基于嵌入的方法使我们能够快速逼近许多分布之间的 Wasserstein 距离，而无需解决成对优化问题。

在第 3 章中，我们首先使用来自图信号处理的思想提出了一种更具可解释性的深度学习架构。一层中的神经元在排列下是无序的和等效的，因此从Run-to-Run可能很难找到负责特定功能的神经元。我们通过在给定神经网络层中的神经元之间施加图结构来向层添加结构。这导致更多可重复和可解释的层，其中神经元将通过打破标准架构中权重对称性而不降低表达性，基于图结构从Run-to-Run执行相同的功能。

在第 4 章中，我们将深度学习的思想引入几何散射。先前的工作表明，几何散射在性能方面与从深度学习文献中开发的当前图神经网络架构具有竞争力 [73]，但对新数据不那么灵活，依赖于许多固定参数。在本章中，我们研究了更灵活的几何散射网络的好处，我们称之为可学习几何散射（LEGS），它允许我们学习固定的散射参数。我们表明这在生物医学图中特别有用，其中有各种各样的图，从小型密集连接图到大型稀疏连接图。事实证明，LEGS 的额外灵活性有助于适应这些不同的数据类型。

在第 5 章中，我们将来自最优传输的想法应用于无监督异常检测问题。这里的目标是给定一个正常点的训练样本，建立一个可以检测异常点的模型。例如，在给定一组狗图像的图像中，检测测试集中的猫。一般来说，这个问题是使用基于重建的方法来解决的，训练一个容量有限的模型来重建训练集，然后根据这个模型重建它们的好坏对测试图像进行评分，这个想法是模型将无法重建远离训练集的点.我们指出了这种方法的三个问题，并提出了一种基于容量受限编码器的不同方法，该编码器直接对输入点进行评分。我们将其与解决 Wasserstein 距离的对偶相关联，并将其应用于理论以提供模型输出的保证。

在第 6 章中，我们将称为连续归一化流 (CNF) [38] 的特定深度学习模型与动态最优传输联系起来。然后，我们使用它来模拟单个细胞随时间的轨迹。当前单细胞转录组测量的一个问题是它们具有破坏性——测量细胞的状态会破坏细胞。这使得随着时间的推移测量单个细胞变得困难。在这里，我们在多个时间点收集人口水平数据，并使用正则化 CNF 推断单个细胞轨迹。我们表明，我们可以根据单细胞时间序列数据更准确地模拟细胞状态随时间的变化。

在第 7 章中，我们将流形上的最优传输与该图上的一系列多尺度扩散联系起来。通过比较图上分布的扩散行为，我们可以快速估计推土机的距离，特别是当我们在 Wasserstein 度量中寻找具有多种测地线地面距离的最近邻分布时。我们展示了如何将现有的多尺度方法推广到推土机的距离计算中，并在将其扩展到图形域的同时提高速度和准确性。

在第 8 章中，我们将第 7 章的工作扩展到不平衡最优传输，它融合了推土机距离（Earth-Mover distance）和无度量的总变化距离。直观地说，这允许创建和销毁（成本）而不是传输质量。我们将这种新的不平衡传输应用于医学概念知识图谱，以理解从患者笔记中提取的概念。

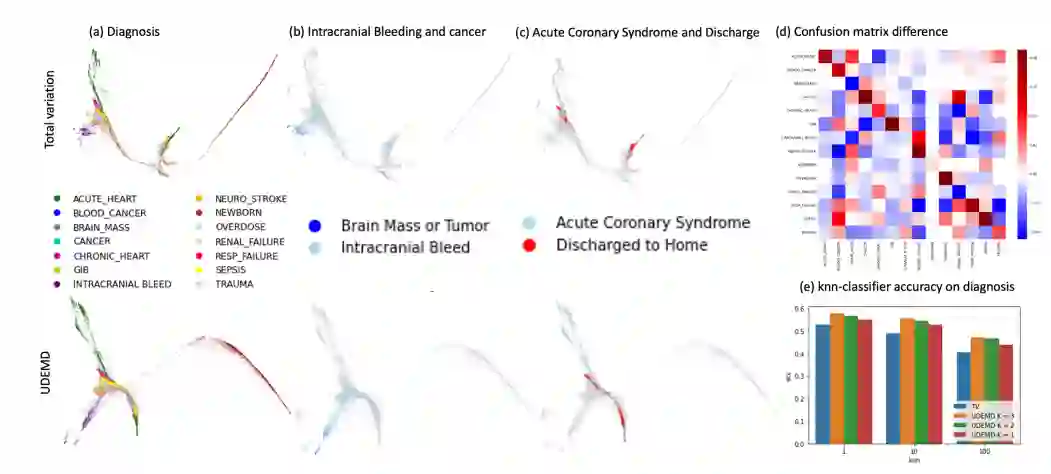
图 8.6：使用 TV 距离（顶部）和 UDEMD 距离（底部）在 Snomed-CT 图上建模为信号的患者嵌入，由患者诊断着色。UDEMD 更好地组织空间，如 (b-c) 中的选定项、(d) 中的混淆矩阵的差异以及 (e) 中诊断的 k-最近邻分类精度所指出的那样。在 (b) 中，请注意 TV 嵌入（顶部）在显示无法通过诊断区分的颅内出血的患者子集之间产生虚假分离（由于信号中的噪声）。另一方面，UDEMD 嵌入（底部）显示了具有此诊断的患者的连续体。对于以绿色显示的脑肿块或肿瘤患者也是如此。(c) UDEMD 嵌入将患有急性冠状动脉综合征的患者组织成一个连续的轨迹，出院的患者（较轻的病例）朝向底部，更严重的病例朝向顶部。TV嵌入再次分裂了这个轨迹。