为什么深度学习泛化性好？Google发布82页《深度学习泛化性揭秘》论文提出相干性梯度理论来解释

深度学习为什么具有很好的泛化性？这个问题得到很多学者的关注。最近Google两位学者提出在于训练过程中不同样例的梯度之间的交互作用来予以解释。值得关注

深度学习中的泛化谜题在于: 为什么经过梯度下降(GD)训练的过参数化神经网络能够很好地对真实数据集进行泛化，甚至它们能够拟合具有可比性的随机数据集?此外，在符合训练数据的所有解决方案中，GD如何找到一个泛化良好的解决方案(当存在这样一个泛化良好的解决方案时)?

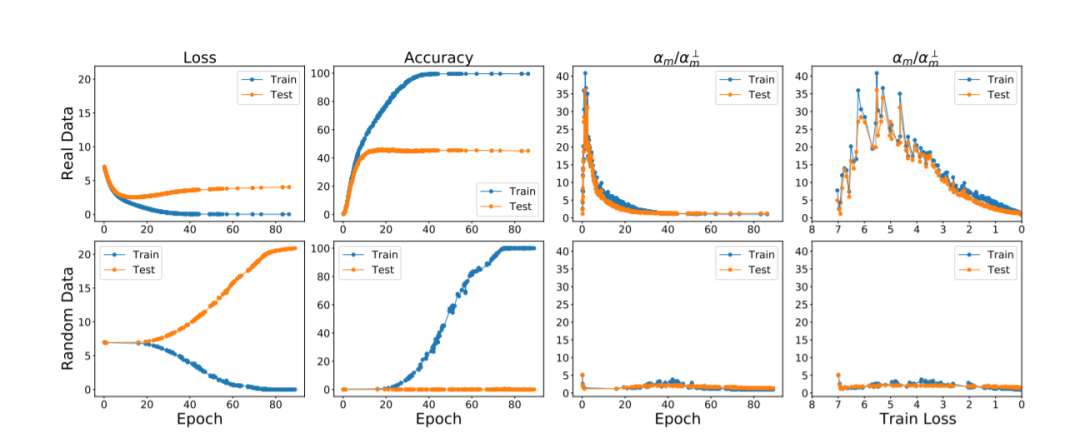
我们认为，这两个问题的答案都在于训练过程中不同样例的梯度之间的交互作用。直观地说，如果每个样例的梯度是良好对齐的，也就是说，如果它们是一致的，那么可以期望GD(在算法上)是稳定的，因此可以很好地泛化。我们用一个易于计算和解释的一致性度量来形式化这个论点，并表明对于几个常见的视觉网络，度量在真实和随机数据集上具有非常不同的值。该理论还解释了深度学习中的一些其他现象，比如为什么一些例子比其他例子更早被可靠地学习，为什么早停止有用，为什么可以从嘈杂的标签中学习。由于该理论提供了一个因果解释，解释了GD如何在存在的情况下找到一个很好的泛化解决方案，它激发了对GD的一系列简单的修改，减少了记忆，提高了泛化。

在深度学习中，泛化是一个极其广泛的现象，因此，它需要一个同样普遍的解释。最后，我们对解决这一问题的其他途径进行了综述，并认为所建议的方法是在此基础上最可行的方法。

引言

**尽管深度学习在实践中取得了巨大的成功，但我们还没有很好地理解它为什么会起作用。**在实践中使用的深度神经网络是过度参数化的，也就是说，它们的参数比用来训练它们的例子的数量要多得多，传统观点认为，这种过度参数化的模型不应该具有很好的泛化性，但它们确实如此虽然我们很早就知道这一认识上的差距(参见Bartlett[1996]和Neyshabur等人[2014])，但在Zhang等人[2017]的一篇有影响力的论文中，该问题得到了尖锐的解决，他们指出，使用随机梯度下降(这是通常的训练方法)训练典型的神经网络，可以很容易地记住一个随机数据集的大小相同的(真实)数据集，他们被设计为。他们认为，这个简单的实验观察对深度学习中所有已知的泛化解释提出了挑战，并呼吁对我们的方法进行“重新思考”。这在社区中引起了很大的努力，以更好地理解为什么神经网络具有泛化性。然而，尽管我们对深度学习的理解由于这一努力而大大提高，但迄今为止，似乎还没有一个令人满意的解释(详细回顾见Zhang et al.[2021])。

在这项工作中，我们的目标是回答由Zhang等人的观察提出的广泛问题，即，为什么神经网络有足够的能力记忆其训练集，但在实践中泛化得很好?****

具体来说，我们想要回答以下问题:

Q1. 通过简单地改变参数化设置中的数据集(例如，从实际标签到随机标签)，我们可以得到非常不同的泛化性能，数据集的什么属性控制泛化差距(当然，假设体系结构、学习率、训练集大小等都是固定的)?我们强调我们的兴趣在于差距，这就是训练和测试损失之间的区别(而不是测试损失本身)。

Q2. 为什么梯度下降不能像记忆随机训练数据那样简单地记忆真实的训练数据?也就是说，在一个过度参数化的设置下，在所有与训练集完美契合的模型中，梯度下降如何找到一个能很好地泛化未知数据的模型呢?这个性质通常称为梯度下降的隐式偏倚。

以往在这些问题上取得进展的大多数尝试都是基于一致收敛的概念[Vapnik和Chervonenkis, 1971]，这是古典学习理论中的主要理论工具。然而，Nagarajan和Kolter最近的一篇论文[2019b]有力地论证了为什么任何基于一致收敛的方法都不太可能解释这一谜题。在本研究中，我们从算法稳定性的角度研究了泛化之谜，虽然这方面的探索较少，但可以说更为普遍[Devroye和Wagner, 1979, Bousquet和Elisseeff, 2002]。我们认为，这两个问题的答案都在于训练过程中样例梯度之间的交互。(样例梯度的相互作用在文献中没有得到太多关注，值得注意的例外是Yin et al. [2018], Fort et al. [2020], Sankararaman et al. [2020], Liu et al. [2020c], Mehta et al. [2021]，我们稍后将对此进行讨论。)

具体来说，我们认为：

1. 当不同样例(训练时)的梯度相似，即存在相干性时，在过参数化设置下的梯度下降具有很好的泛化效果。

2. 当有相干性时，梯度下降的动力学会产生稳定的模型(即不太依赖任何一个训练实例的模型)，稳定的模型具有很好的泛化性。