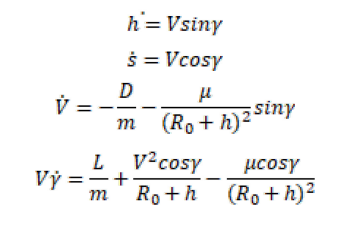本研究提出了一种方法,用于训练和验证数据驱动的、参数化的、多保真的减序模型,能够预测具有不连续特征的高维空气热流场。在设计新概念时,设计者往往缺乏进行传统概念设计所需的历史数据,因此必须依赖基于物理学的模型和模拟工具的数据。然而,现实的计算预算往往限制了可用于训练预测模型的高保真样本的数量。在这些情况下,多保真方法已被确定为提高模型准确性的关键推动力,因为它们能够利用来自高保真和低保真来源的训练数据,这使设计者能够使用大量廉价的低保真样本来补充训练数据并提高采样分辨率。这项研究制定了一种方法,利用Procrustes流形排列,用线性和非线性投影方法进行多保真模型的减序。然后将这些方法应用于陆军海军的Finner射弹,以在学科和系统层面上描述这种方法。据观察,所提出的模型阶次还原能够准确地捕捉表面分布。当部署在一个耦合轨迹模型中时,减序模型能够在模拟中取代全序CFD,同时与全序解决方案保持密切一致。所提出的方法也优于传统的空气动力学数据库查询表,同时保持可控的计算成本。
技术途径
降维
降序建模是一种广泛的方法,它寻求确定高维数据集的低维表征,尽可能准确地捕捉原始数据中观察到的相关行为(Maaten, et al., 2009)。降维(DR)算法通常用于减少原始模型的自由度数量,以获得一些低维表示,被称为潜空间,它保留了原始数据集的一些质量,如观察到的协方差或成对距离(Xiao, et al., 2017)。然后,原始的高维训练数据被投射到这个低维的潜空间中,以便在进行预测时可以识别和利用数据的主导特征。ROM可以分为侵入式和非侵入式,前者意味着它们必须与分析的管理方程对接,并且经常需要修改源代码(Lucia & Beran,2003),后者意味着它们只使用输入和输出数据进行训练(Chen,2012)。由于现代高超音速系统的高度多学科性,设计者在早期设计阶段使用 "黑盒"分析代码是很常见的。出于这个原因,非侵入式ROM通常是航空航天应用的首选(Rajaram, et al., 2020)(Xiao, et al., 2017)。
文献中已经开发了许多非侵入式的ROM技术,每个技术都有不同的假设,即如何最好地识别和描述训练集的基本行为(Maaten, 等,2009)。线性方法,如主成分分析(PCA)(Tropea, et al., 2007),可能是最常用的技术,并已在航空航天应用中成功使用了几十年(Iuliano & Quagliarella, 2013)(Jolliffe, 1986)(Lumley, 1967)。利用非线性降维(DR)的ROM,如基于歧义学习的ROM(Franz, et al., 2014),最近被使用,因为它们能够比线性对应技术更有效地捕捉不连续的流动特征,如冲击(Decker, et al., 2021)。
使用Procrustes分析的流形对齐
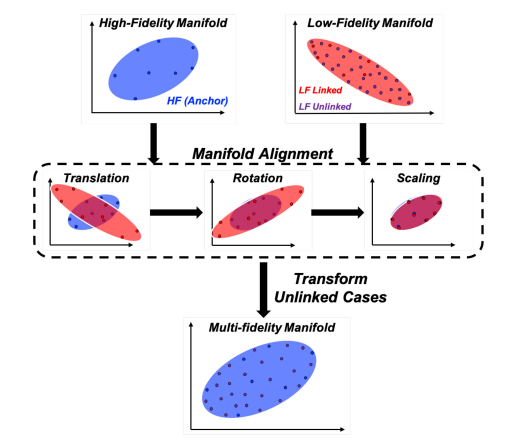
为了使前面讨论的方法适用于CFD解决方案,必须以相同的网格尺寸、节点连接和基础物理模型拍摄快照。Manifold Alignment(MA)被认为是增强这些单保真ROM技术的关键因素,因此它们可以利用多保真来源的数据(Wang & Mahadevan,2009)(Wang & Mahadevan,2008)。这使得在训练预测模型时,只要每个数据集的基础系统是相关的,就可以同时利用来自不一致配方的数据集(Perron, et al., 2020)。特别是,Procrustes MA已被证明在构建多保真ROM方面表现良好,因为它能够利用来自不一致来源的数据,而不需要修改原始训练集(Perron, et al., 2020)。(Decker, et al., 2021)开发了MA在CFD ROM中应用的数学公式。
图2:使用Procrustes分析的流形对齐的概念说明。
降阶建模方法
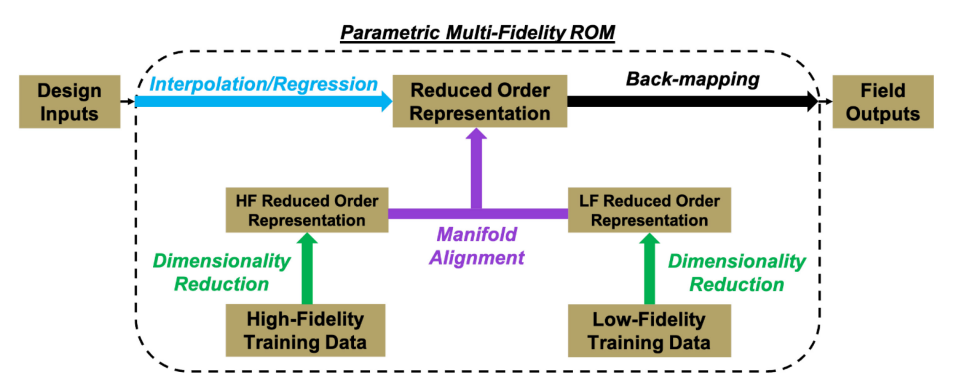
这种方法的结果是遵循图3所示结构的场代理。在这些模型中,DR被用来识别捕捉每个数据集的基本行为的潜在空间。通过减少每个保真度级别的数据得到的潜空间使用MA进行融合。在实践中,这个潜空间具有足够低的维度,多保真插值或回归技术(如CoKriging(Han等人,2012))可以用来预测未见设计点的潜空间坐标。有了这些预测的潜空间坐标,就可以通过一个叫做Back-mapping(Franz, et al., 2014)(Decker, et al., 2021)的过程构建高维领域的预测。
图3:多保真ROM结构的说明。
轨迹分析
一旦空气动力学的ROMs被训练出来,它们就可以被部署在一个耦合的分析框架中以评估它们的性能。在这项研究中,进行了滑行轨迹分析。高超音速飞行器的轨迹对高水平的性能目标有重大影响,并推动了其他几个学科的关键边界条件。任务优化是必要的,以确定特定飞行器的最佳性能。由于这些原因,滑行轨迹分析是一个有用的测试案例,以评估所提出的方法的实用性。
文献中已经开发了许多方法来解决高超音速滑翔轨迹。工程中感兴趣的问题往往过于复杂,无法用变分法分析解决,因此需要数值方法(Rao,2009)。已经开发了一系列被称为直接方法的数值方法,这些方法将轨迹离散化,并使用一个称为转录的过程将最优控制问题转换为非线性编程(NLP)问题,可以通过直接优化解决(Rao,2009)(Ross & Fahroo,2002)。在直接方法家族中,有两类主要的解决方法:射击法和同位法。射击法通过显式积分治理方程来传播轨迹,而配位法通过将治理方程视为离散域内每一点的平等约束来隐式执行治理方程(Von Stryk & Bulirsch,1992)。射击法对参数化简单的问题表现良好,并允许使用高阶数值积分方案,而配位法由于现代NLP求解器的鲁棒性和利用数值稀疏性的能力,被认为对更复杂的问题效果良好(Rao,2009)。出于这个原因,本研究中使用了直接配位来进行轨迹分析。
为了解决这些问题,轨迹分析是用Dymos(Falck, et al., 2021)实现的。Dymos建立在OpenMDAO(Gray, et al., 2010)的基础上,利用伪光谱配位技术来进行优化。问题使用IPOPT算法(Wachter, 2002)解决,该算法在pyOptSparse框架(Perez, et al., 2012)中实现(Wu, et al., 2020)。
在这项研究中,运动方程是针对球形、非旋转地球上的二维飞行路径而实现的: