AAAI 2024 | 通用图扩散框架

题目：A Generalized Neural Diffusion Framework on Graphs 作者：李一博，王啸，刘洪瑞，石川单位：北京邮电大学，北京航空航天大学前言：近期许多研究都揭示了图神经网络（GNN）与扩散过程之间的联系，并且提出了许多基于扩散方程的GNN。因为这两种机制紧密相关，所以我们思考一个根本性的问题：是否存在一个通用的扩散框架，可以统一这些 GNN？这个问题不仅可以加深我们对 GNN 学习过程的理解，而且可能会指导我们设计一系列新型 GNN。在本文中，我们提出了一个带有保真项的通用扩散方程框架，正式建立了扩散过程与更多GNN之间的关系。同时，通过这个框架，我们发现了图扩散网络的一个特性，即当前的图扩散网络仅对应于一阶扩散方程。然而，通过实验研究，我们发现高阶邻居的标签呈现相似性。这一发现给了我们设计新的高阶邻居可知的扩散方程的灵感。基于该框架，我们提出一种新型图扩散网络（HiD-Net）。HiD-Net对攻击的抵抗能力更强，并适用于同质图和异质图。

1. 背景与动机

图在现实生活中随处可见，而GNN可以高效地完成各类图上的任务。近期一些研究表明，GNN本质上和扩散方程密切相关，图上的消息传递过程可以视作一种消息扩散。扩散方程提供了一种新的连续的视角来解释GNN，并且可以启发新的GNN架构设计。随着越来越多基于扩散方程的GNN架构的提出，我们需要一种形式化的方法来建立各类GNN和扩散方程之间的联系。这将帮助我们更好地理解GNN，并启发我们设计新的GNN架构。

2. 图上的扩散方程

扩散方程用于物质在不同浓度区域间通过扩散作用进行转移的过程，被定义为：其中，

是浓度。
是时间。
是扩散系数，代表物质的扩散速率，通常是常数或是由时间和位置决定的函数。
代表散度。散度是各方向二阶导之和。
是浓度的梯度，即浓度的变化速率。

该方程左边是浓度的变化速率，右边是各个方向上浓度差异的和。即某位置浓度的变化速率取决于该位置浓度与各个方向上浓度的差异之和。以一个简单的链式图为例，我们将该扩散方程类比到图上。我们首先定义图上的一阶导和二阶导。

在图上我们将节点的特征类比为“浓度”。第个节点的特征为，位置上的一阶导为和。我们进一步定义图上的二阶导（即一阶导的差）为：。链式图上只有一个方向，所以。而在一般的图上有多个方向，则。我们进一步对该式做正则，得到, 其中是矩阵中的元素, 。所以节点上的扩散方程可以定义为：该式描述了时刻节点的特征变化速率，指出节点和周围邻居的特征差异越大，那么其特征变化速率也越大。

3. 通用图扩散框架

然而，的变化速率不应该只取决于节点和周围邻居节点的特征差异，否则就会导致过平滑的现象，即节点所有节点的特征都变得相似。的变化应该也取决于节点的初始特征。如果和的特征差异比较小，那么的变化速率也应该比较小。所以我们加上了一个保真项，提出了我们的通用扩散框架：

为系数。

我们进一步有两点发现： 1. 该通用扩散框架可以从一个能量方程推出： 1. 该框架与许多GNN紧密联系，如GCN/SGC，APPNP，GAT，AMP，DAGNN等，如：

SGC/GCN上的扩散方程为： * APPNP上的扩散方程为：

4. 高阶图扩散网络

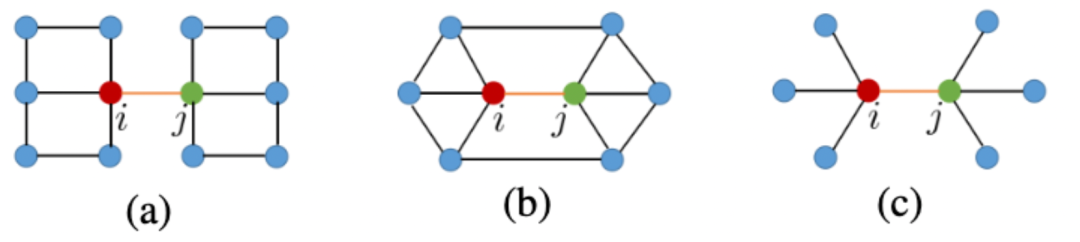
在一阶扩散过程中只考虑了节点的一阶邻居。如上图所示，三个图中的节点完全相同，虽然结构不相同，但是从节点到节点的扩散流完全相同。但我们希望扩散过程能捕捉这个结构差异，让节点到节点的扩散流不同。所以我们需要提供额外的信息。我们测试了节点的不同阶邻居与其的标签相似程度。

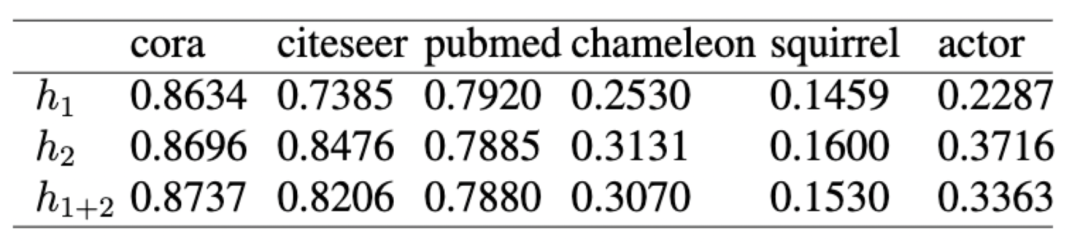
如上表所示，衡量的是节点和第阶邻居的标签相似程度。可以看到二阶邻居和节点也具有很高的相似性。所以我们希望利用二阶邻居提供更为丰富的信息。因此我们重新定义一阶扩散流为：高阶扩散方程即为：这个过程为基于扩散的消息传递范式(DMP)，好处有两点：

二阶邻居可以节点周围的局部环境。即使一阶邻居有异常特征，这个影响也可以通过考虑更大的邻居范围来缓解
二阶邻居提供了和标签相关的额外信息，这样即使一阶邻居倾向于异配，我们也可以通过利用二阶邻居的信息来做出正确的预测。

最终我们提出了我们的模型HiD-Net：

5. 实验

数据集：同质图：Cora，Citeseer，PubMed，异质图：Chameleon，Squirrel，Actor Baseline：选取了传统GNN：GCN，GAT，APPNP，基于扩散的GNN：GRAND，GRAND++，DGC，ADC。

5.1 节点分类

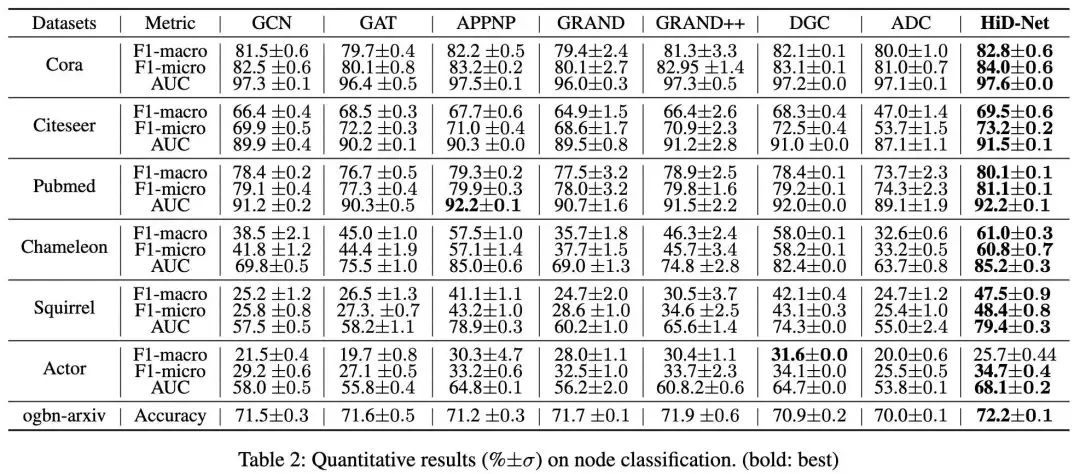
如上表所示。可以看到我们的模型相比其他baseline取得了更好的效果，尤其是在异配图上。

5.2 鲁棒性分析

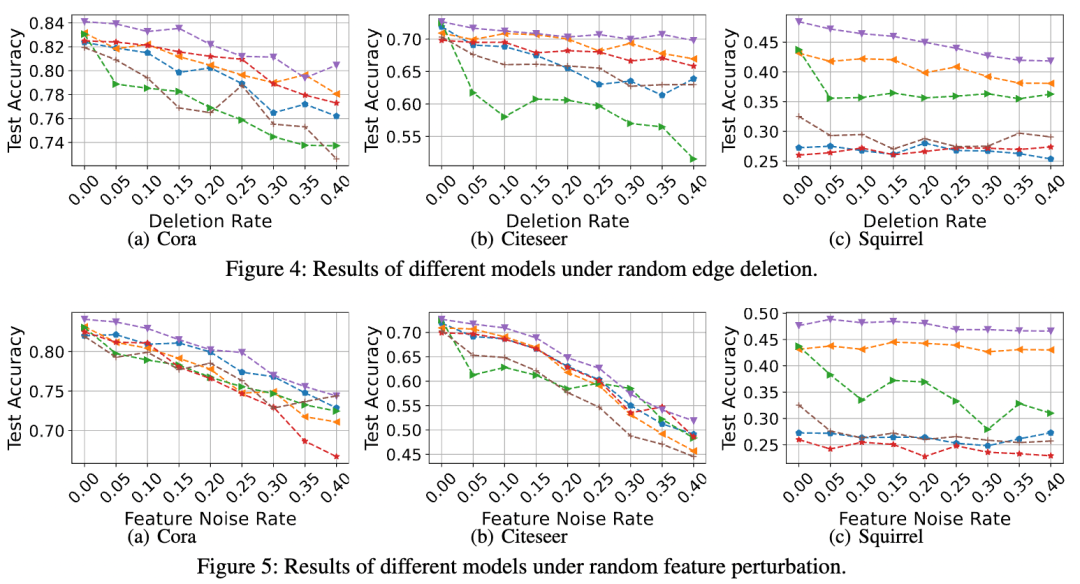
我们的模型利用了二阶邻居，因而能更好地处理特征和结构异常的情况。我们分别对边和特征做了扰动，观察我们的模型和其他baseline在不同扰动程度下的表现。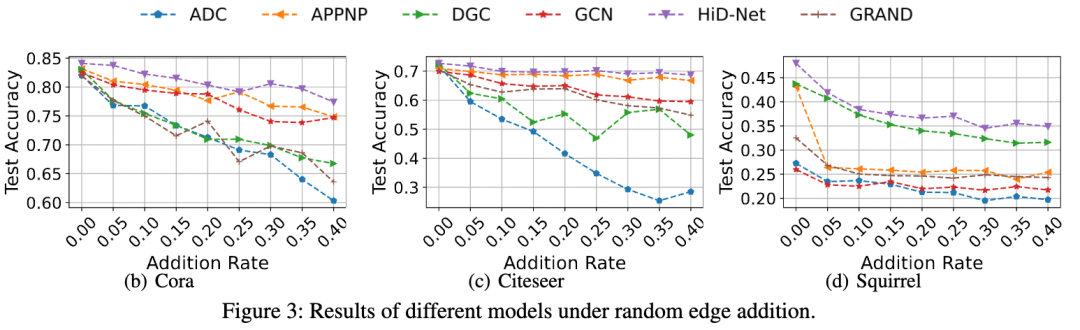

如上图所示，可以看到我们的模型相比其他baseline在扰动的情况下性能下降较少，因而更鲁棒。

5.3 过平滑分析

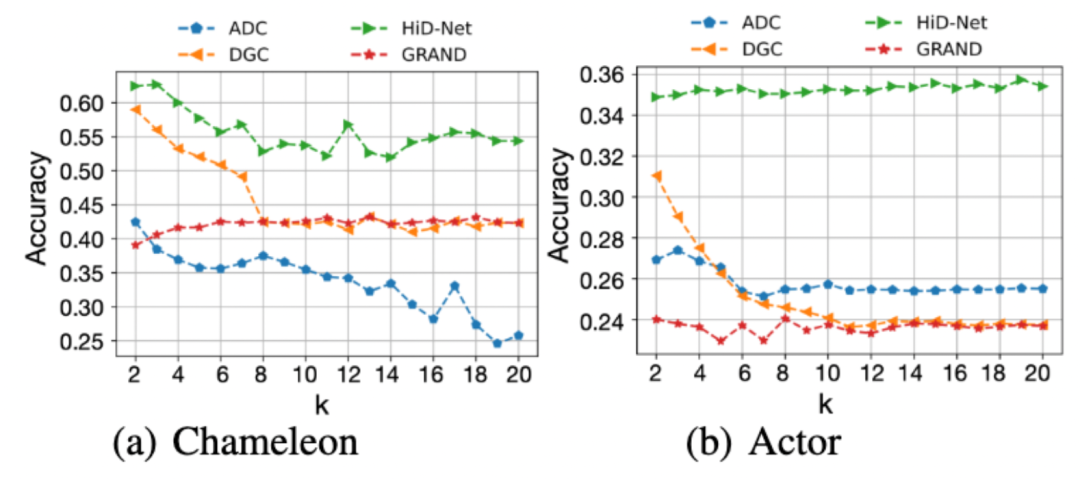
为了证明我们的模型相对其他基于扩散的GNN能更好地解决过平滑的现象，我们测试了在不同层数下的表现。

如上图所示，可以看到随着层数的增加，我们的模型能取得更好的效果。

6. 结论

在这篇论文中，我们提出了一个通用的扩散图框架，建立了不同图神经网络与扩散方程之间的关系。基于该框架我们发现当前的图扩散网络主要考虑一阶扩散方程。我们发现二阶邻居蕴含丰富的信息，因而提出一个新的高阶扩散图网络（HiD-Net）。HiD-Net在同质图和异质图上都更加鲁棒和通用。广泛的实验结果验证了HiD-Net的有效性。我们的工作正式指出了扩散方程与广泛多样的GNN之间的关系。考虑到以往的GNNs主要是基于空域或谱谱域设计的，这个新框架可能会开启一个理解和推导新型GNN的新路径。

本期责任编辑：杨成本期编辑：岳大帅

北邮 GAMMA Lab 公众号

主编：石川责任编辑：杨成编辑：岳大帅

长按下图并点击“识别图中二维码” 即可关注**北邮 GAMMA Lab **公众号