GNN在非欧式空间如何表达？【TPAMI2021】双曲深度神经网络研究综述

2021 年 12 月 29 日 专知

【导读】关于双曲神经网络综述论文。

近年来，双曲深度神经网络(HDNNs)在双曲型空间中的深度表示提供了维数较少的高质量嵌入，特别是对于具有层次结构的数据。这样的双曲神经体系结构迅速应用到不同的科学领域，包括自然语言处理、单细胞RNA序列分析、图形嵌入、金融分析和计算机视觉。有希望的结果表明，它优越的能力，显著的紧致性的模型，相比欧几里德空间的模型有更好的物理解释。为了促进未来的研究，本文对构建HDNN的神经成分进行了全面的综述，并对目前主要的双曲空间深度研究方法进行了推广。它还介绍了各种任务的当前应用，以及富有洞察力的观察和确定开放的问题和有前途的未来方向。

树形结构和层次结构的数据在自然场景和现实世界的[1]、[2]、[3]、[4]中普遍存在。很多这样的数据，例如，互联网[5]，大脑网络[6]，世界贸易网络[7]和金融网络[8]，表现出高度非欧几里德潜伏解剖和负弯曲属性[9]，[10]，[11]。在推荐系统[12]、社交媒体分析[13]、知识图嵌入[14]、单细胞RNA序列分析[15]、图像检索[16]等任务中都可以观察到类似的属性。与此同时，当前的机器学习，特别是深度学习[17]已经提供了一种强大的数据驱动方式来分析和理解数据。其核心是期望学习数据的低维和语义丰富的表示。深度神经网络具有多层结构，具有数百万个参数，并以全面和高度优化的深度学习库[18]，[19]，[20]为载体，理论上具有适应任何复杂函数的潜力，促使了许多研究领域的主导地位，比如图像分类[21]，[22]，机器翻译任务[23]，甚至玩电子游戏[24]。

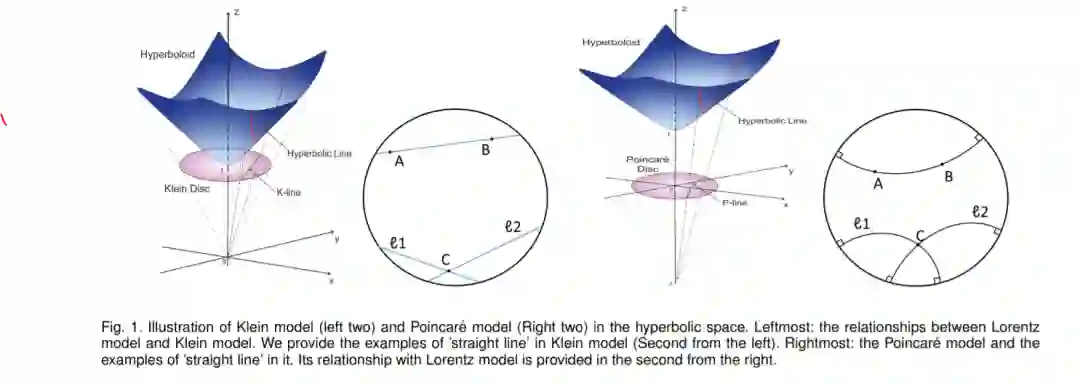
然而，在这些成功的应用中，欧几里德空间中的常规网格数据，例如文本和图像，是主要的焦点。此外，学习过程是在直观友好的欧几里德空间中进行的，欧几里德空间是一个曲率为零的平坦空间。然而，在欧几里德空间中运行的神经体系结构严重依赖于局域性，并且最初是为网格数据设计的，因此不一定为非欧几里德空间中的结构化数据提供最强大或最有意义的几何表示。一般情况下，应考虑非欧几里德空间，包括常正曲率的椭圆空间[25]和常负(截面)曲率的双曲空间[26]。椭圆空间中的神经网络[27]，[28]，[29]，[30]，利用球面调和变换或基于拉普拉斯图卷积，已成功地应用于球面信号。与此类似，对于具有层次结构的数据，人们强烈希望在双曲空间中构建神经网络，因为层次结构可以在这种空间中以低失真[31]表示。

除了结构化数据外，常规样本与重要发展进展之间的潜在关系也可以用双曲空间中的层次结构来建模。从认知科学的角度来看，人们普遍认为人类使用等级来组织行为[32]和对象类别[33]，[34]，[35]。一项有趣的研究[36]发现，自然气味和人类对气味的感知描述都可以用三维双曲空间来描述。在单细胞分析中，细胞发育过程显示出强烈的层次关系，可以用双曲空间[15]来描述。Zhou等人[37]也发现遗传变异及其表达可以用低维双曲几何建模。有趣的是，目前的研究[16]甚至发现miniImageNet[38]和CIFAR[39]的特性具有明显的双曲性质，这些特性是通过使用VGG[40]、Inception[41]和Resnet[21]等神经体系结构在欧几里得空间中学习的。因此，构建双曲型深度神经网络(hypercurve deep neural network, HDNN)对于有效地处理更复杂的不规则数据，解释和推理超出欧几里德空间的更复杂关系，从而在双曲型空间[31]，[42]中取得成功是非常必要和有利的。

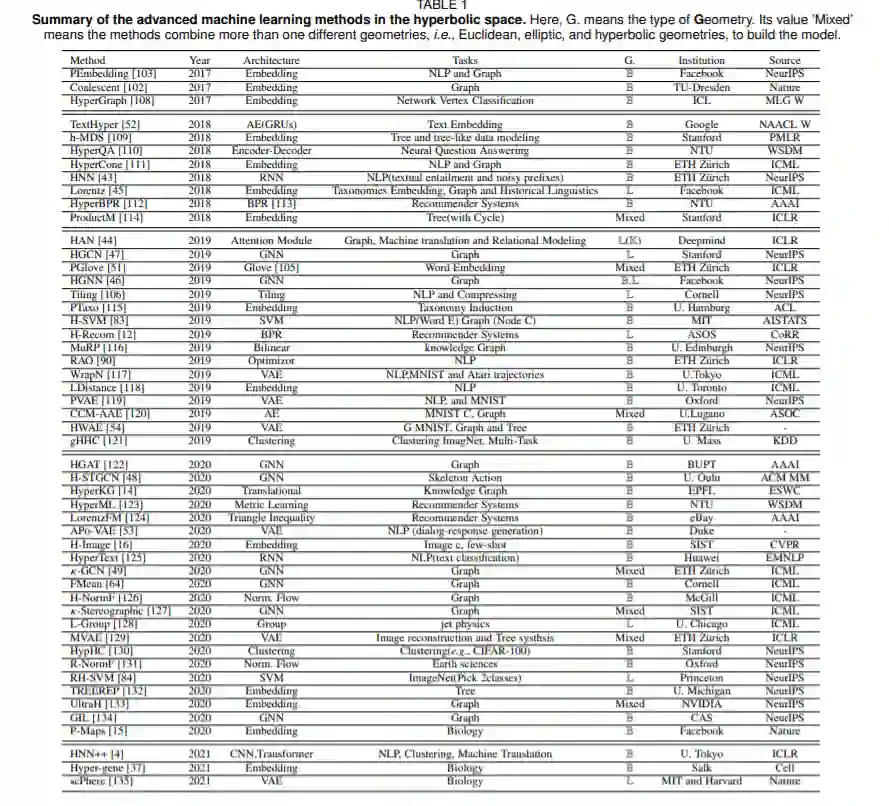
最近，为了解决各种不同的机器学习任务，开发了众多的HDNN架构[4]、[43]、[44]、[45]、[46]、[47]、[48]、[49]、[50]。双曲空间已经被提出作为一种连续学习数据层次表示的替代方法，从文本的[51]，[52]，[53]和图结构的数据[46]，[48]，到生物的[15]，[37]和图像的[16]，[54]。这一兴趣的原因是双曲度规近似指数展开的系统的可能状态描述的层次树状过程。双曲空间的负曲率导致了截然不同的几何性质，这使得圆的周长和圆盘的面积随着半径r呈指数增长，而不是像欧几里德空间那样只能线性和二次增长。因此，双曲空间最近获得了在显示出某些理想的几何层次特征的空间中建模数据的势头。

综上所述，利用双曲深度神经网络来表示数据有几个潜在的优势:

模型的泛化能力更强，过拟合更少，计算复杂度更低，对训练数据的要求更低。
低失真嵌入，保留了局部和全局的几何信息。
一个更好的模型理解和解释，可以提供一个正形映射到欧几里德空间，这样它是友好的下游任务。

虽然近年来在双曲空间中构造神经网络得到了广泛的关注，但这是一项极具挑战性的任务，因为欧几里德神经算子在空间中并不总是有效。将欧几里得运算，从基本算术运算(如加法和乘法)，到神经运算(如卷积和运算)，再到双曲空间，都是非常困难的。据我们所知，这一领域还没有关于双曲型深度神经网络的研究。本文首次尝试并旨在提供一个全面的文献综述双曲深度神经网络的机器学习任务。我们的目标是:1)提供一个简明的背景和解释，使读者熟悉双曲几何的基础知识，2)回顾当前有关双曲深度学习算法和应用的文献，3)确定开放的问题和有前途的未来方向。