IJCAI2022 Oral: 探究和解释图像分类任务中存在的频域偏见

作者：林致宇，高逸飞，桑基韬*

单位：北京交通大学，鹏城实验室 论文链接：https://arxiv.org/pdf/2205.03154.pdf 代码地址：https://github.com/zhiyugege/FreqBias *通讯作者

1、简介

卷积神经网络（CNN）在各种任务上已经表现出接近人甚至超越人的表现，研究[1]指出，CNN在处理视觉信息机制上与人类视觉系统存在差异，这导致CNN常有“超人”的表现，例如：CNN倾向于使用纹理信息进行图像分类，而不是像人一样利用形状信息[2]。针对这些差异表现，[3]在频域角度提供了一个有趣的结论：CNN能利用人不可见的图像高频信息进行模型泛化，同时CNN捕获图像频域分量的行为能够部分解释模型的一些反直觉表现，例如泛化性高而对抗鲁棒性差。

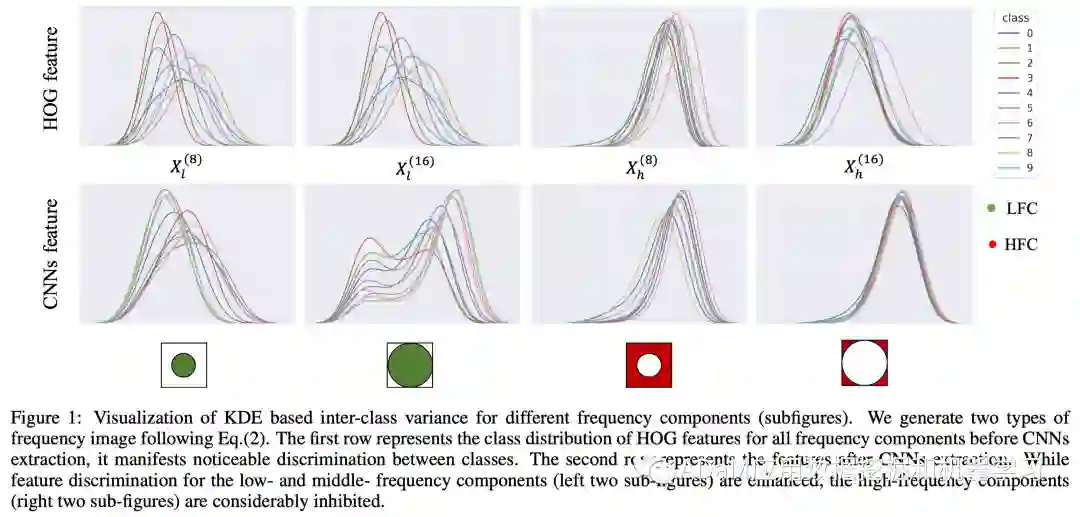
本论文旨在研究图像分类任务下CNN在频域空间的表现。首先我们在探究频域特征空间的过程中发现了一个有意思的现象：图像频域分量在经过CNN的特征提取后（HOG特征CNN特征），低频分量的类间差异被放大（图1左两列），而高频分量的类间差异被抑制（图1右两列）。

这一现象表明CNN在中低频图像分量上表现出了比高频图像分量更强的学习偏好，这启发我们探究CNN学习机制下更基本的频域偏见现象和现象背后的原因。本论文具体贡献可以归纳为以下两个方面：

为了研究图像分类任务中的频域偏见现象，我们从特征判别性（feature discrimination）和学习优先级（learning priority）两方面提供了新的偏见观测结果。这两个观测结果相互关联，共同为现有研究中关于泛化性偏见的结论提供了补充视角。

我们从频谱密度（spectral density）和类一致性（class consistency）两个方面给出频域偏见原因的假设，实验结果表明：数据集频谱密度主要影响学习优先级，而类一致性主要影响特征判别性。

2、符号定义

表示给定数据集中的图像-标签对，表示CNN特定中间层的特征，其中为特征的维度。表示CNN的输出，其中为类别数，由此我们定义损失函数为。在本论文中，我们使用二维离散傅里叶变换（简称DFT）进行频域分析，，分别表示离散傅立叶变换和离散傅立叶逆变换。通过以上变换，输入图像可以被分解为低频图像分量,和高频图像分量,具体定义如下：

其中表示给定频率半径的掩码矩阵，我们定义低频和高频的掩码矩阵如下： 由此：

频谱密度定义为径向频率上的方位角积分 其中。

3、探索频域偏见的现象

3.1 特征判别性偏见

本节通过基于KDE的类间方差（inter-class variance）估计来观察不同频域分量的特征判别性偏见现象。

**3.1.1 基于KDE方法的类间方差计算

考虑在第个类别特征空间的第维特征，采样个特征并组成集合，特征点的核密度估计为： 所有特征维度上的特征分布集合可以被视为类特征分布的估计值。通过计算两个类在所有维度的特征分布曲线之间的重叠面积比的均值来估计类间方差，具体如下： 类间方差表示为：

**3.1.2 结果&讨论

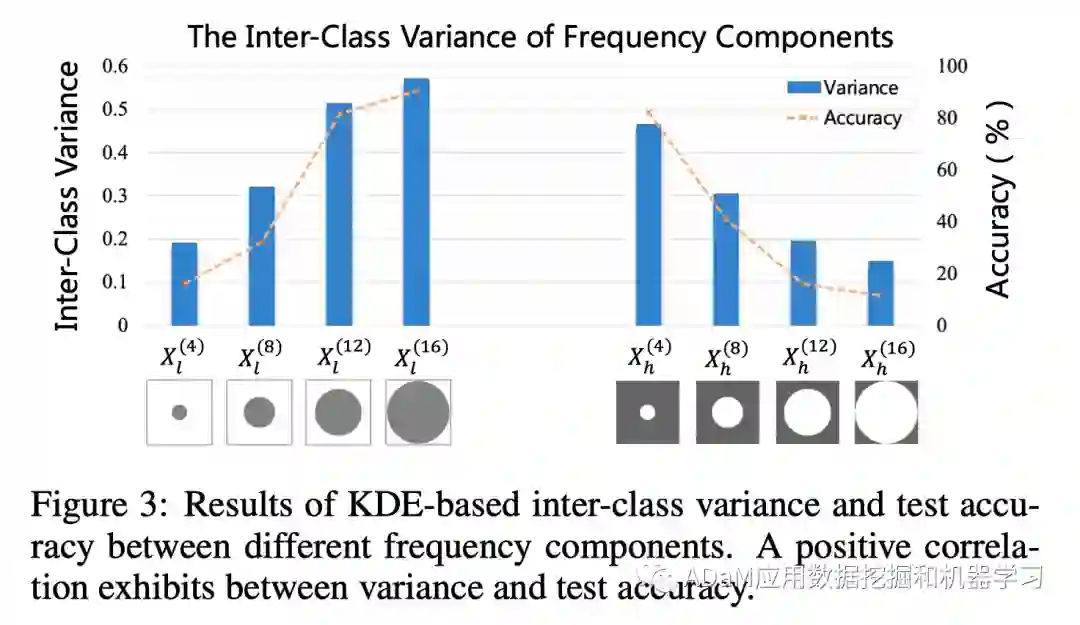
图中第一个值得注意的现象：特征判别性在不同频域分量之间表现出显著的差异。具体而言，中低频分量的特征的类间差要显著大于高频分量的特征类间差。这一结果从特征粒度揭示了模型的对频域信息的利用偏见现象。 * 另一个有价值的发现是频域分量的特征判别性和测试准确率呈现正相关性。不难理解，高判别特征对模型泛化性的贡献更大，同时说明我们提出的特征判别性偏见支持和解释了之前研究工作[3,4]中观察到的泛化性偏见。

3.2 学习优先级偏见

本节通过评估输入图像的梯度频谱（gradient spectrum）观察训练过程中不同频域分量的学习优先级偏见。

**3.2.1 频域分量的梯度评估

在图像分类任务中，的测量为我们提供了有关空间域图像对损失函数的贡献的信息。在本论文中，关注的重点从空域转移到频域，即度量输入图像中部分频域分量对损失的贡献：（表示保留频段信息的图像），以观察模型对频域信息的学习优先级。为了探索图像中所有频段分量的学习优先级同时降低计算复杂度，我们提出以下命题，详细证明过程在附录可见。 **Proposition：**表示输入图像，表示保留给定频段的掩码矩阵，我们通过以下公式建立空域梯度谱和频域梯度谱的联系： , 其中定义为梯度频谱。 基于以上命题，我们在训练的每个步骤中计算梯度频谱，并进行可视化。

**3.2.2 结果&讨论

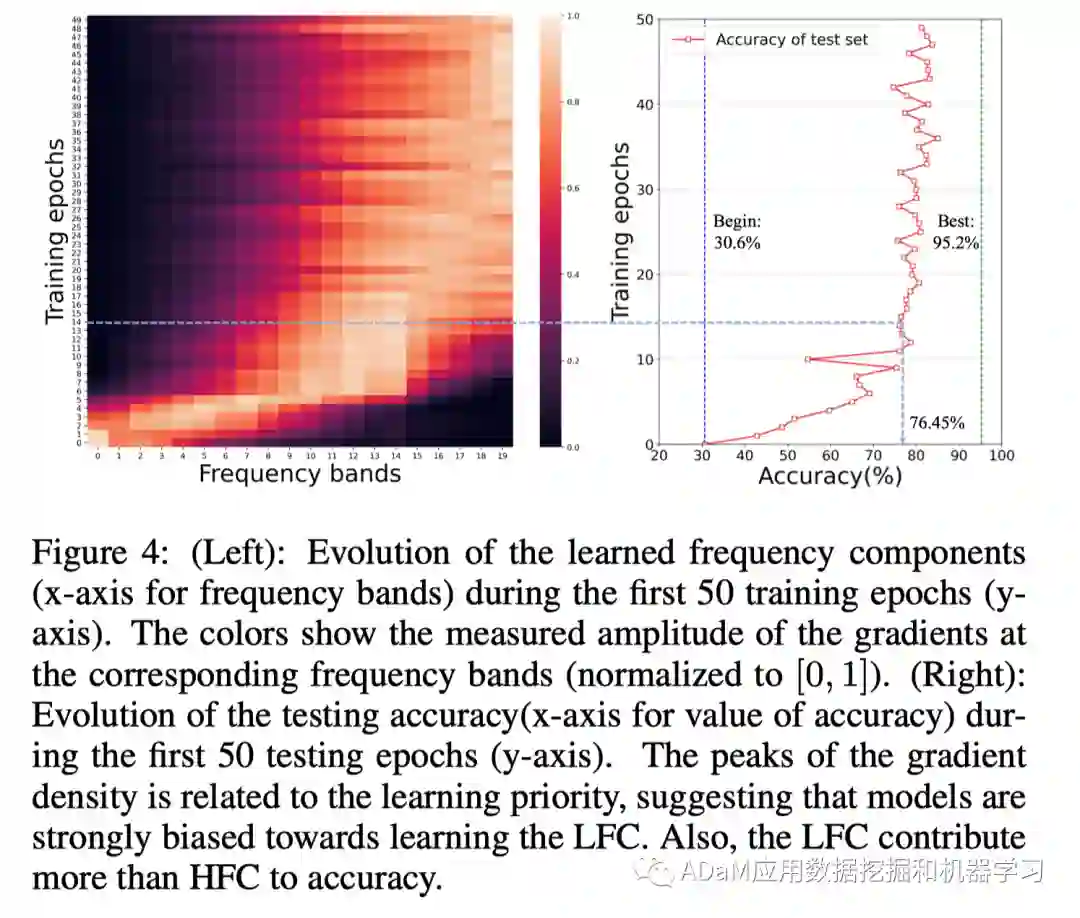
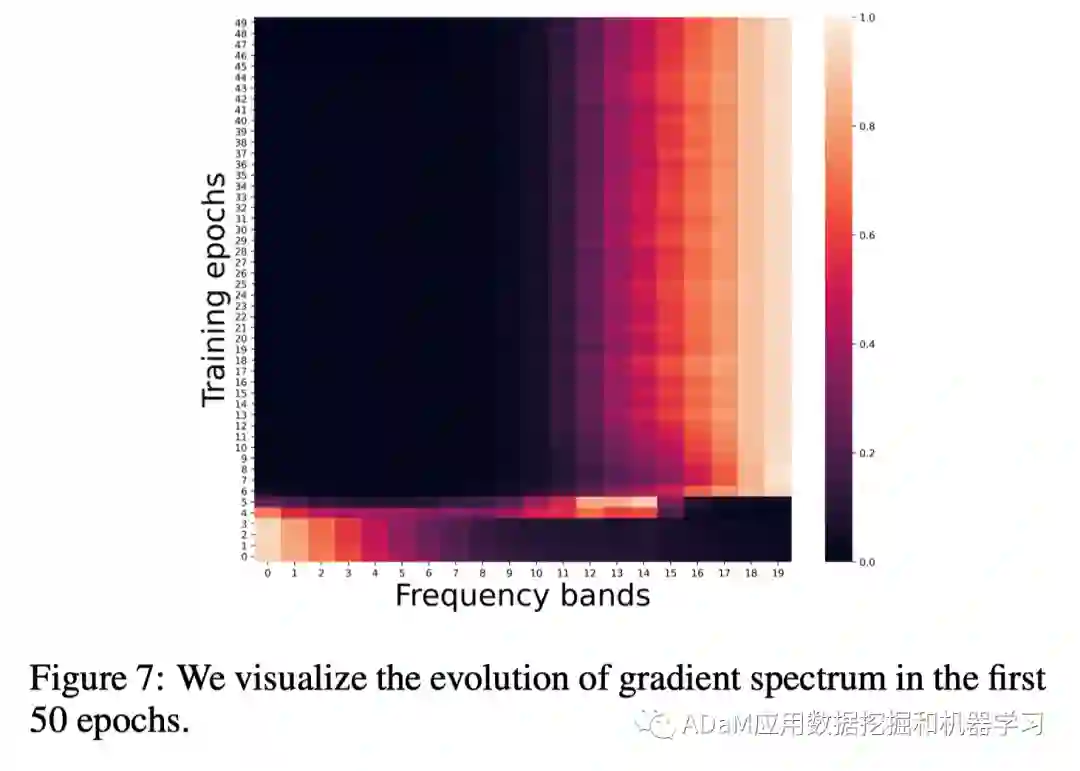
• 在每个训练过程中，梯度谱峰值主要集中在某几个特殊频段而不是均匀分布在所有频段；随着训练的进行，梯度谱峰值从低频逐渐向中频移动，最后停留在高频。梯度谱的演化揭示了频域信息学习优先级的偏见现象：模型更倾向于优先学习低频信息。
• 模型快速（前15个训练步骤）拟合中低频信息，且达到较高的泛化性（76.45%）;相反，模型利用更多的时间拟合高频信息，但是精度收益有限（76.45% to 95.2%）。以上观察表明，在低频信息上的学习优先级偏见有益于提高模型的泛化能力。

4、频域偏见背后的假设

4.1 频谱密度假设

我们假设频谱密度（spectral gradient）是图像分类任务中频域偏见现象的影响因子，并提出了基于卷积操作的密度增强策略（CDES），用于修改自然图像的频谱密度。

**4.1.1 CDES

该策略的核心思想是提高高频区域的密度峰值，具体算法流程： 1、通过卷积核的卷积操作使生成图像的频谱密度与设计的目标频谱密度对齐，卷积核训练过程的损失函数如下：

上式中代表卷积操作后的新生成图像，代表目标频谱密度。

2、 为了保证低频分量的一致性，用原始图像的低频分量替换生成图像的低频分量： 实验中，我们设置并训练了两组卷积核，在cifar10数据集基础上生成了两个变体数据集：中添加的高频信息包含了类别强相关的信息，中添加的高频信息包含了类别弱相关的信息，并在此基础上训练了分类器：,, 。

**4.1.2 偏见现象分析

从特征判别性和学习优先级两个角度给出现象和分析：

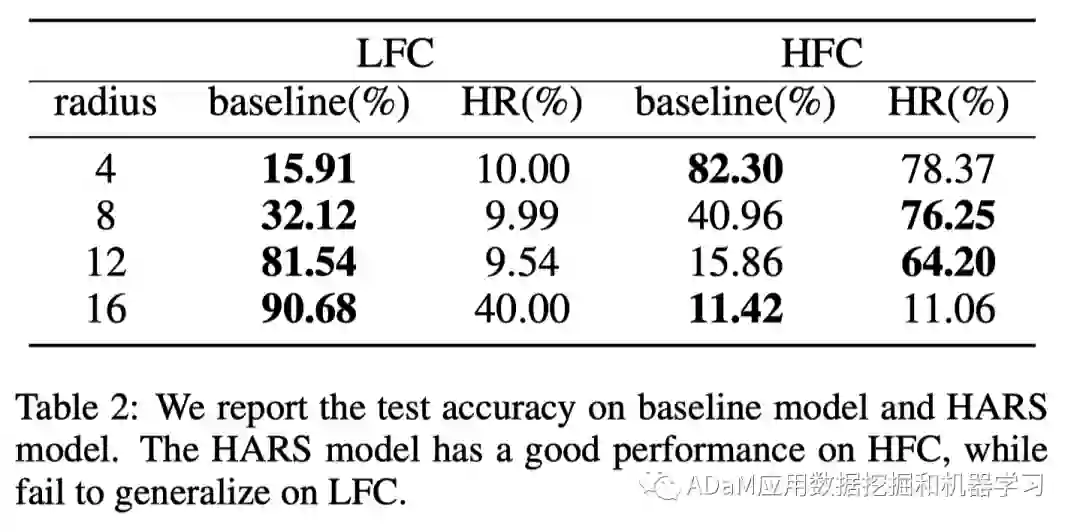
特征判别性: 测试3个数据集中高频分量图像的准确率，实验结果如上表所示。我们发现 显著提升了高频图像的泛化精度，而却严重抑制了高频信息的表达，我们分析现象产生的原因是与添加的高频信息中类信息强弱相关。实验结果表明：频谱密度不是影响特征判别性的唯一因素。

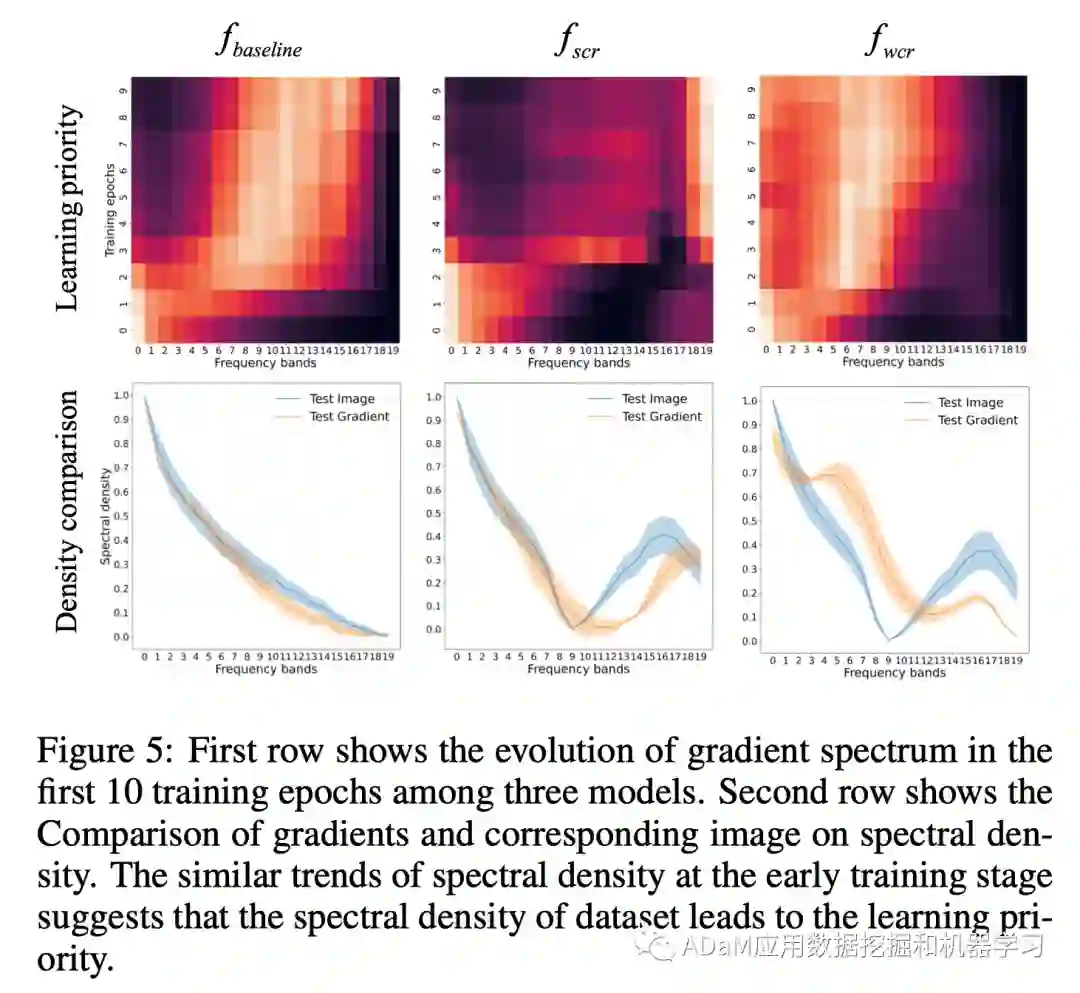
学习优先级：我们可视化了3个数据集在学习过程中的梯度频谱的演化情况（上图第1行），一个有趣的现象是，在训练初期，和的学习优先级表现出了相似性并和表现出了差异。在第2行，我们进一步发现图像的频谱密度与梯度的频谱密度的演化趋势呈现出几乎一致的趋势。这表明，早期训练阶段的学习优先级偏见现象是由在数据集中图像的频谱密度决定的。

上述观察和分析验证了我们的假设，即数据集的频谱密度很好地解释了学习优先级现象，但不是特征判别性的充分条件。

4.2 类一致性假设

这一节旨在类一致性的角度解释频域偏见现象。我们假设模型在分类任务中只利用具有类一致性属性的频域分量

**4.2.1 基于频域空间的数据增强方法分析

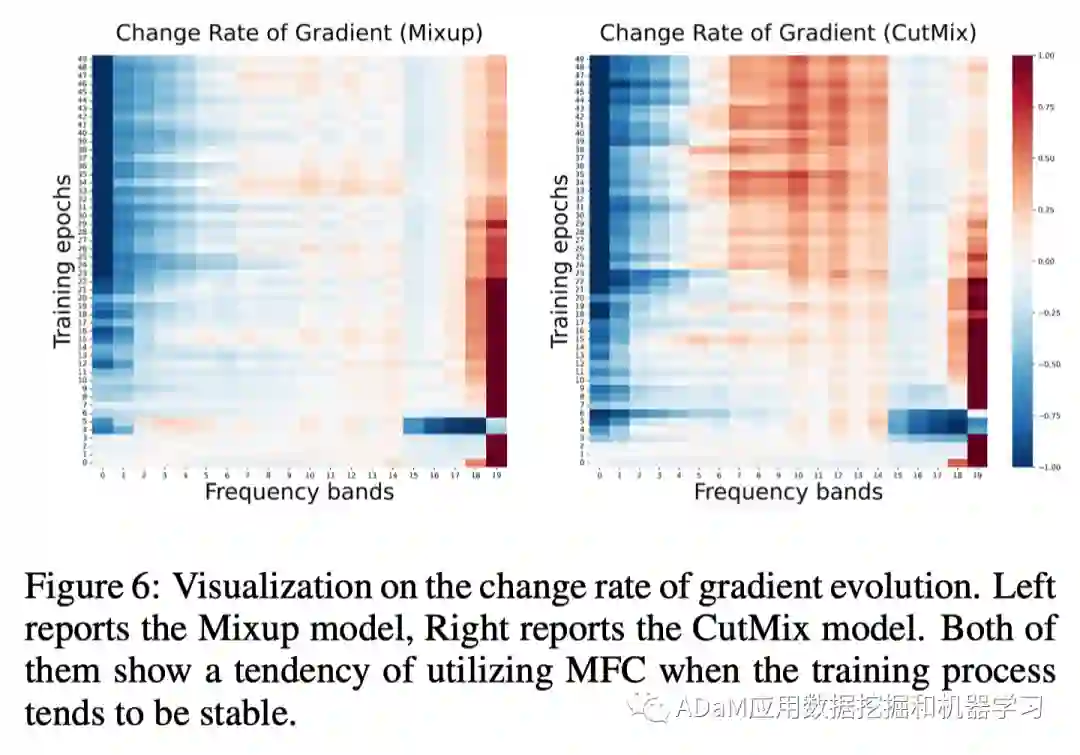
由于数据增强是增强类一致性的重要手段，首先尝试从频域角度了解其有效性和出色的性能。我们探究了Mixup[5]和CutMix[6]对学习过程中不同频段信息梯度频谱密度的影响，计算其相比标准模型的变化率并可视化：

结果表明，数据增强模型提高了对中频分量的利用：当训练过程趋于稳定时，中频分量的梯度密度有一个明显上升的趋势。在频域分量的泛化性结果也得到了一致的结论。

**4.2.2 基于频域重组的数据增强

为了验证类一致性假设，我们构建了cifar10数据集的另一个变体数据集。在我们构建数据集的策略中，扰动了由人工标注建立的低频和标签的类一致性，图像仅保留高频信息和标签的类一致性。模型在变体数据集训练后在标准的测试集上进行测试，在特征判别性和学习优先级的结果上有了如下有趣的发现：

特征判别性：如表所示，标准测试集上高频的分量的泛化性显著提高，这表明重组数据集有效地提高了模型对于高频分量的利用和高频分量的特征判别性。

学习优先级：

• 尽管我们扰动了低频分量的类一致性，模型仍然会保持低频分量在训练初期的学习优先级。考虑到我们并没有改变图像的频谱密度，我们认为这一现象很好地支持了我们对频谱密度的假设
• 相比标准的训练过程，我们发现模型更早地开始关注高频信息。

上述观察和分析验证了我们关于类一致性的假设。

结论：

本文研究并解释了图像分类中的频域偏见现象。我们通过对特征辨别性和学习优先级的观察扩展了频域偏见现象。进一步讨论和假设验证了导致频域偏见现象的可能原因。在解决频域偏见问题并用于实际模型改进之前，还有更多可探索的方向。一些未来的工作包括但不限于：（1）需要从模型的角度分析更多的原因，例如，局部感受野和分层表示是否有利于高频特征提取。（2）需要在高频分量和中低频分量之间取得平衡，即在不破坏中低频分量利用的情况下增强模型对高频信息的利用。(3) 我们在初步观察中发现，抑制的高频特征与对抗鲁棒性密切相关。这启发我们：频域偏见是否能够为泛化性-鲁棒性权衡问题提供解决思路。

参考文献

[1] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. IEEE, 2016. [2] K. L. Hermann, T. Chen, and S. Kornblith. The origins and prevalence of texture bias in convolutional neural networks. 2019. [3] H. Wang, X. Wu, Z. Huang, and E. P. Xing. High-frequency component helps explain the generalization of convolutional neural networks. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. [4] Antonio A. Abello, Roberto Hirata, and Zhangyang Wang. Dissecting the high-frequency bias in convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, pages 863–871, June 2021. [5] Hongyi Zhang, Moustapha Cisse, Yann N Dauphin, and David Lopez-Paz. mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412, 2017. [6] Sangdoo Yun, Dongyoon Han, Seong Joon Oh, Sanghyuk Chun, Junsuk Choe, and Youngjoon Yoo. Cutmix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 6023–6032, 2019.