IJCAI'21 | 理解GNN的"弱点"

2021 年 11 月 26 日 图与推荐

1Understanding Structural Vulnerability in Graph Convolutional Networks

论文标题：Understanding Structural Vulnerability in Graph Convolutional Networks
作者：Liang Chen, Jintang Li, Qibiao Peng, Yang Liu, Zibin Zheng, Carl Yang
单位：中山大学，Emory University
论文链接：https://www.ijcai.org/proceedings/2021/310
代码链接：https://github.com/EdisonLeeeee/MedianGCN

今天介绍的是中山大学图学习团队被 IJCAI'21 会议接收的一篇论文：「Understanding Structural Vulnerability in Graph Convolutional Networks」。国际人工智能联合会议（International Joint Conference on Artificial Intelligence, 简称为IJCAI）是人工智能领域中最主要的学术会议之一，位列CCF-A，2021年的论文接受率为13.9%。文章重点关注图卷积网络的鲁棒性问题，基于崩溃点（breakdown point）理论解释了图卷积网络容易受到攻击的原因，并基于此提出两种更加鲁棒的图卷积方法。

2前言

近年来，图卷积神经网络被广泛用于各种图结构数据的学习任务上，并在各个领域中取得了优异的表现。尽管图卷积网络已经在各个领域取得了一系列成功，有大量文献指出其存在结构脆弱性问题，这使得通过修改图中少量的边或节点信息就能够使得图卷积网络输出错误的结果。更甚者，攻击者可以不需要知道模型的参数也能够发动有效的攻击。

图卷积网络脆弱性的特点限制了其在实际中的广泛应用。为了提高图卷积网络的鲁棒性，一系列防御方法被提了出来，包括对抗学习，迁移学习，鲁棒性验证等，并且有效地提高了模型的鲁棒性。然而，以往的研究大多倾向于从实验性的角度去解释图卷积网络的脆弱性归因，并没有尝试去揭示图卷积网络容易受到攻击的本质原因。文章尝试从另一个新的角度去解释图卷积网络的脆弱性，并给出如下结论：图卷积网络的脆弱性主要归因于不鲁棒的聚合函数。在文章余下的内容，作者从理论与实验的角度提供了支撑这一结论的依据。

3图卷积网络

这里首先回顾一下图卷积网络(Graph Convolutional Networks, GCN)。假设表示一个图，其中为节点集合，为边集，并且存在节点特征集合。一个层的GCN定义为：

其中，与为每一层的节点表示(embedding)以及经过线性层与激活层输出后的表示。为聚合函数，这里以最常用的GCN为例：

4实证研究分析

文章的这一节以一个简单的小实验着手。通常来讲，攻击者的目的就是在给定攻击成本的情况下去近似最强的攻击扰动，从而给模型造成最大的破坏性。在这个实验中，文章通过枚举所有可能的扰动观察是否可能改变GCN对目标节点的预测类别。具体地，扰动包括增加一条边(Injection)，删除一条边(Deletion)，以及增边和减边同时使用的方法(Both)。

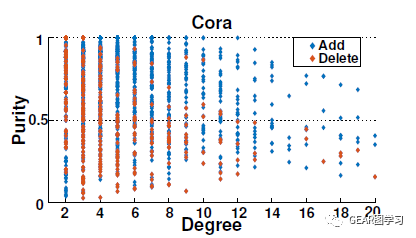
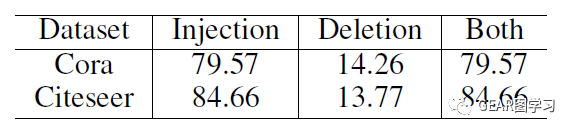
图1展示了攻击成功的节点的度和纯净度(purity)分布情况，纯净度(purity)定义为节点两跳邻居内与其相同类别的节点所占的百分比。表1则展示了两个数据集上三种不同方法攻击成功的节点百分比。从上述实验可以得到如下结论：（1）修改一条边能够攻击成功大多数节点，即使这些节点的度和纯净度(purity)都较高。（2）增加一条边的攻击效果比减少一条边的攻击成功率更高，也就是Injection是比Deletion更强的攻击操作。这一结论也于之前的研究相符。

5鲁棒性分析

根据上一节的实验性分析，可以发现增加边的操作是比删除边的操作更能够攻击成功GCN。那么，为什么往图中增加边能够攻击GCN呢？作者以一张图举例：

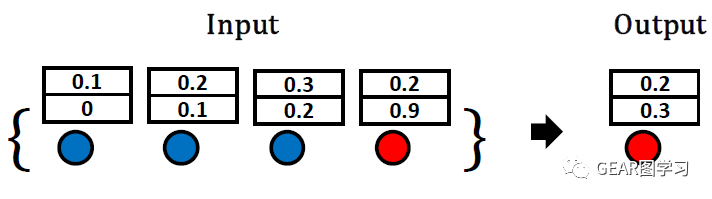
通过图2的简单例子可以看到，使用均值聚合函数的GCN在目标节点邻域注入一个恶意节点（也就是增加了一条边），而这个节点在特征上与其余正常节点分布差异较大，通过均值聚合后改变了GCN的聚合结果。

接着，文章借鉴了鲁棒统计学领域的崩溃点（breakdown point）理论进行分析：

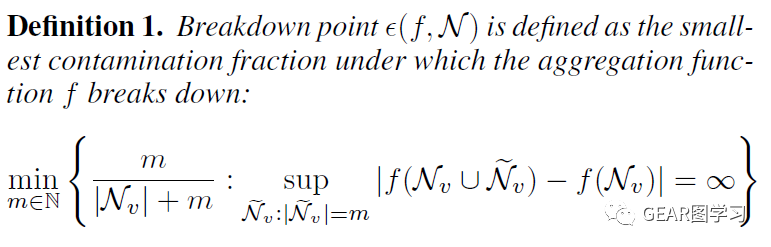
简单解释下，崩溃点（breakdown point）理论就是衡量一个函数在受到数据扰动情况下鲁棒性情况。崩溃点（breakdown point）可以直观地理解为：最少需要往数据中添加数量为的数据点，能够使得函数的输出变化为无穷大。

我们假设攻击者可以添加的扰动数量不超过，因为如果异常数据超过正常数据，那么就难以区分「正常」与「异常」了。基于崩溃点（breakdown point）理论，可以发现均值函数是不鲁棒的。在最坏情况下，只需要往数据中加入一个值为无穷的点，即可使得模型的输出变化为无穷大。 因此，均值函数的崩溃点为最小值，其中为目标节点的邻居节点。

回到GCN的模型分析，在受到扰动的情况下，我们将GCN的聚合过程分解为如下两部分：

由于GCN中的聚合权重总是正数，的输出与扰动后的节点表示呈线性相关。因此仅需要添加一个特征差异非常大的节点，就可以使得GCN输出错误的预测结果。通过上述的分析也揭示了为何基于均值聚合的GCN容易受到结构性扰动攻击，并且删除边的攻击效果远远不如增加边的效果。因为即使攻击者删除了一半的边，也不会使得均值函数的输出改变为无穷大。

基于此，文章提出了两种鲁棒的聚合函数来提高GCN的鲁棒性。

中值聚合函数(median)

显然，从统计学角度上来看，中值函数的鲁棒性是远远高于均值函数的，通过崩溃点（breakdown point）理论分析我们也可以发现，中值函数的崩溃点为最大值1/2，也就是攻击者需要添加一半以上的扰动才可能成功改变输出结果。

截尾均值聚合函数(trimmed mean)

截尾均值函数可以看成是均值函数的改进，也就是我们平时在比赛打分经常用到的：去掉一部分最大值和最小值评分，最后取平均。通过这种方式，能够很大程度上减少打分的偏差，从而得到更加公平的结果。在统计学中，截尾均值函数也是另一个鲁棒的函数，其崩溃点至少为，其中为数据点的数量，为去掉的最大值和最小值百分比。

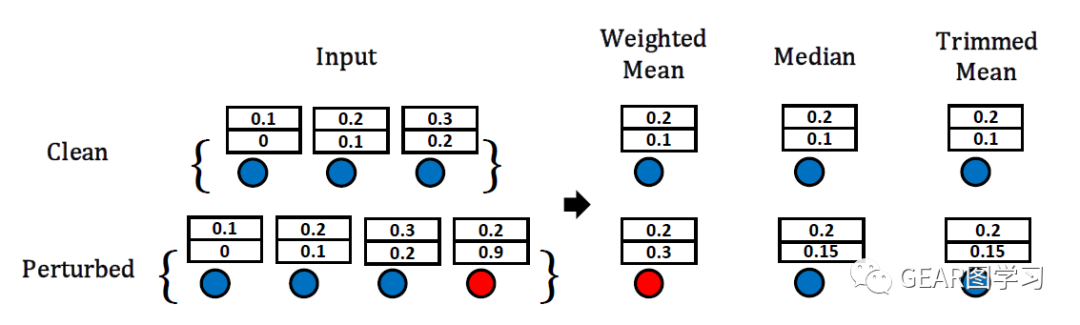
最后，文章通过图3说明了三种聚合函数的在受到攻击前和攻击后的输出，可以发现：在没有受到攻击的时候(clean)，三种聚合方式都能够输出正常的结果；在受到攻击后(perturbed)，均值聚合函数的输出变化较大，而其余两种鲁棒聚合函数则受到的影响较小。

6实验

作者在四个引文数据集上进行了实验，数据集信息如表2所示：

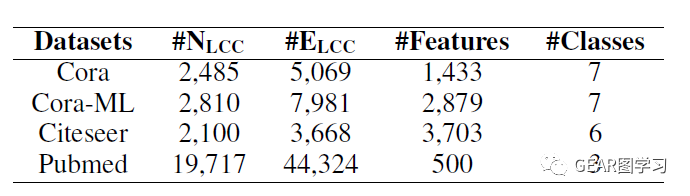
文章follow了2018年KDD Zügner et al.的文章，对每个图进行了预处理，仅取最大联通子图(largest connected component, LCC)进行实验。数据集划分为10%训练，10%验证，80%测试。文章设置的攻击场景为两种：直接攻击与间接攻击。直接攻击为扰动添加的边可以直接作用到目标节点上，而间接攻击则相反，扰动不能直接影响目标节点。通常直接攻击的效果是远远好于间接攻击的，但是间接攻击会更具有隐蔽性。

文章基于中值聚合函数与截尾均值聚合函数提出了两个鲁棒聚合模型：MeidanGCN (median)和Trimmed GCN (TMean)。由于防御模型不仅需要聚焦于鲁棒性，还需要保持在原始数据集上的性能（防止模型过度拟合扰动数据），因此实验分别从攻击前和攻击后进行分析。

6.1攻击前实验

攻击前，可以发现文章提出的两种方法都没有影响GCN的性能。

6.2攻击后实验

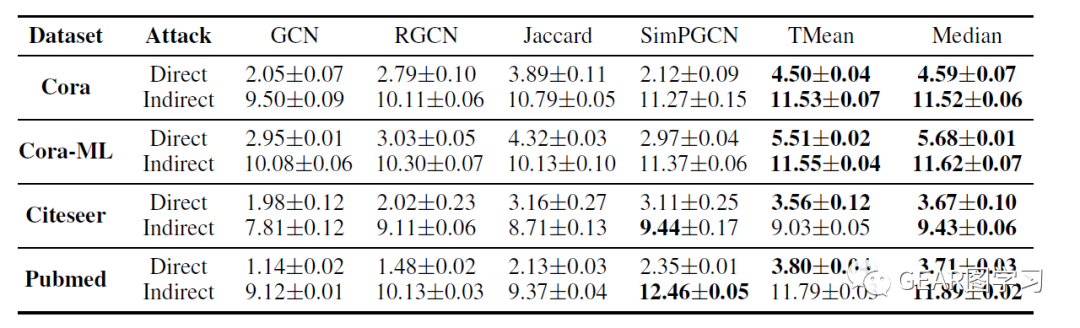
作者采用来衡量模型的鲁棒性，具体计算方式为，也就是当攻击的扰动从1-5的时候模型分类准确率的加权和。可以发现，在攻击后，GCN的鲁棒性远远低于其余防御方法，而文章提出的两种模型在直接攻击场景下取得了最优的鲁棒性，并且在间接攻击的场景下也大多数鲁棒性最优。

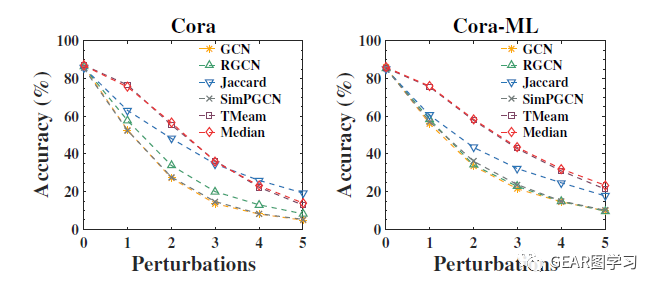
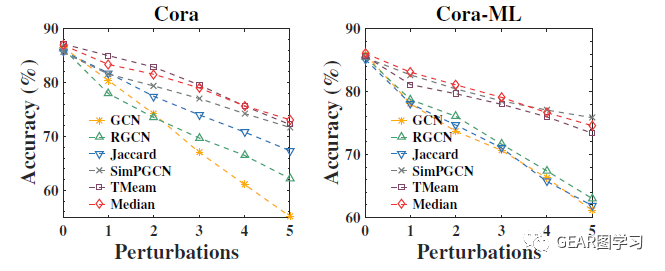
从图4和图5可以看见，在扰动情况较低的条件下，文章提出的两种模型准确率都远远高于其余方法，而随着攻击扰动的强度增大，这一差距在逐渐减小。这是由于图中节点的度都较小（大约3左右），攻击达到3以上则已经破坏了崩溃点理论的假设（扰动不超过1/2），因此模型难以区分正常和异常结点。然而在这种情况下，模型的准确率仍然高于其它方法。

7总结

本文研究了图卷积网络容易受到攻击的原因，并基于崩溃点理论与实验结果给出了解释：图卷积网络的脆弱性主要来自于不鲁棒的聚合函数。基于这一发现，文章进一步提出了基于中值聚合函数与截尾均值聚合函数提出了两个鲁棒聚合模型：MeidanGCN (median)和Trimmed GCN (TMean)，在四个数据集的实验中说明了所提方法的有效性，从而验证了文章的结论。