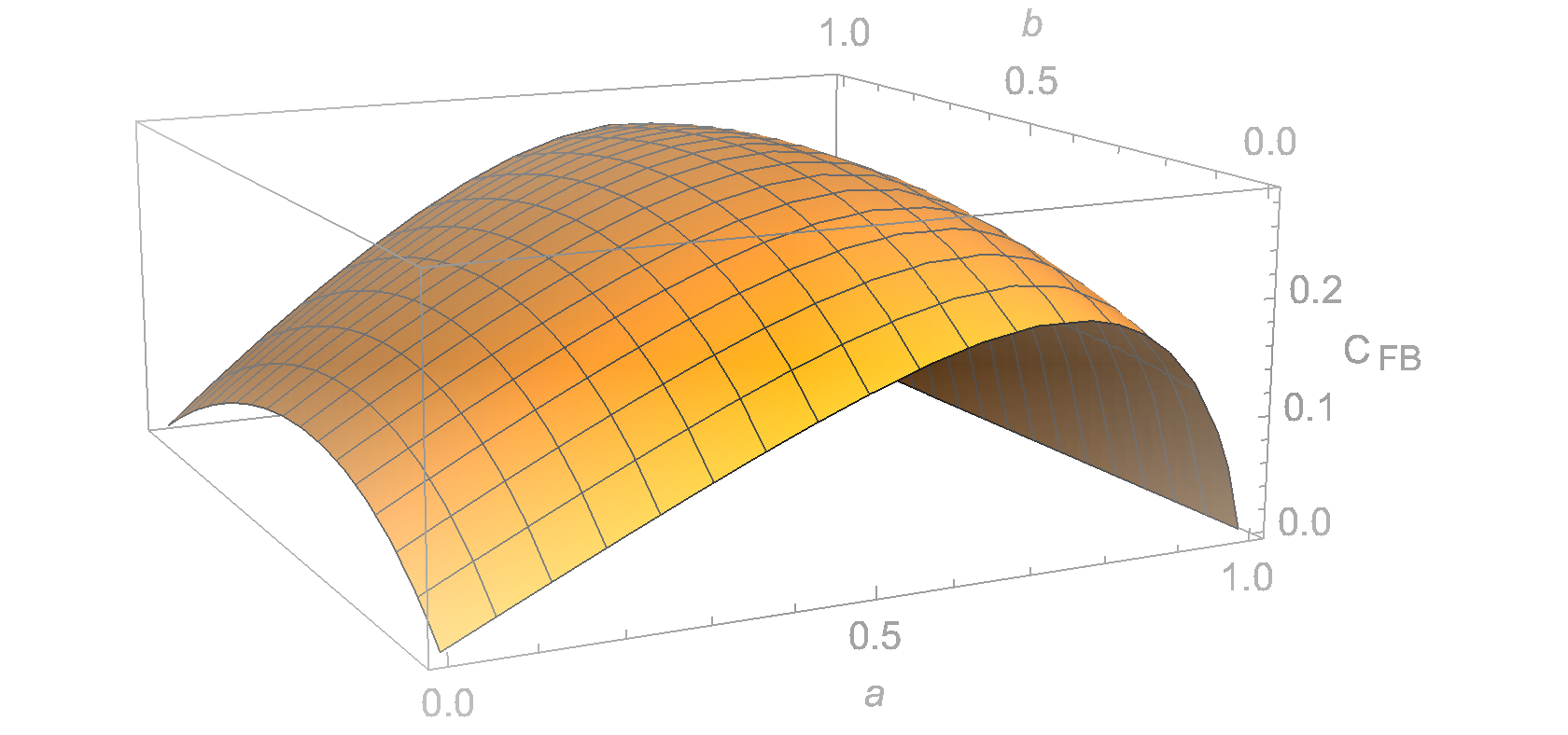
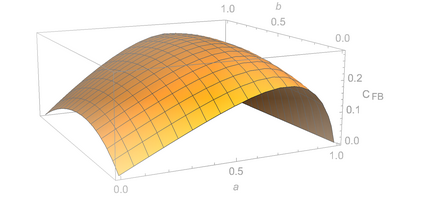
We consider finite-state channels (FSCs) where the channel state is stochastically dependent on the previous channel output. We refer to these as Noisy Output is the STate (NOST) channels. We derive the feedback capacity of NOST channels in two scenarios: with and without causal state information (CSI) available at the encoder. If CSI is unavailable, the feedback capacity is $C_{\text{FB}}= \max_{P(x|y')} I(X;Y|Y')$, while if it is available at the encoder, the feedback capacity is $C_{\text{FB-CSI}}= \max_{P(u|y'),x(u,s')} I(U;Y|Y')$, where $U$ is an auxiliary RV with finite cardinality. In both formulas, the output process is a Markov process with stationary distribution. The derived formulas generalize special known instances from the literature, such as where the state is i.i.d. and where it is a deterministic function of the output. $C_{\text{FB}}$ and $C_{\text{FB-CSI}}$ are also shown to be computable via convex optimization problem formulations. Finally, we present an example of an interesting NOST channel for which CSI available at the encoder does not increase the feedback capacity.
翻译:我们考虑的是频道状态取决于先前频道输出输出的有限状态频道( FSCs ) 。 我们称之为 Nosy 输出是STate (NOST) 频道。 我们以两种情况来获取NOST 频道的反馈能力: 在编码器( CSI) 中, 有或没有因果状态信息( CSI) 。 如果 CSI 不可用, 反馈能力是 $C ⁇ text{F ⁇ \\\\\\\\\\\\\\(x ⁇ y) } I(X); Y ⁇ Y”, 而如果在编码器中, 反馈能力是 $C ⁇ text{FSI {FSI} 。 在两种公式中, 输出进程是带有固定分布的Markov 进程。 衍生公式概括了文献中已知的特殊实例, 例如, 状态是 {FSI}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\