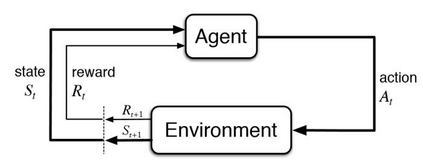
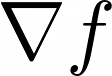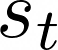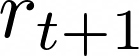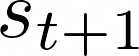Maximising a cumulative reward function that is Markov and stationary, i.e., defined over state-action pairs and independent of time, is sufficient to capture many kinds of goals in a Markov Decision Process (MDP) based on the Reinforcement Learning (RL) problem formulation. However, not all goals can be captured in this manner. Specifically, it is easy to see that Convex MDPs in which goals are expressed as convex functions of stationary distributions cannot, in general, be formulated in this manner. In this paper, we reformulate the convex MDP problem as a min-max game between the policy and cost (negative reward) players using Fenchel duality and propose a meta-algorithm for solving it. We show that the average of the policies produced by an RL agent that maximizes the non-stationary reward produced by the cost player converges to an optimal solution to the convex MDP. Finally, we show that the meta-algorithm unifies several disparate branches of reinforcement learning algorithms in the literature, such as apprenticeship learning, variational intrinsic control, constrained MDPs, and pure exploration into a single framework.
翻译:在基于强化学习(RL)问题拟订的Markov决策程序(MDP)中,将累积奖励功能最大化(Markov)和固定的,即界定为州-行动对对和时间独立的累积奖励功能,足以在基于强化学习(RL)问题的制定基础上,捕捉到许多类型的目标。然而,并非所有目标都可以以这种方式捕捉到。具体地说,很容易看到,以固定分布的连接函数表示目标的Convex MDP无法以这种方式总体地形成。在本文中,我们重新将 convex MDP问题作为政策和成本(负奖励)参与者之间的一个微积分游戏来描述,并提出了解决该问题的元-algorthm。我们表明,由成本玩家产生的政策的平均水平,即最大限度地增加成本玩家产生的非固定的奖励,与 convex MDP 的最佳解决方案一致。最后,我们表明,元-alphymorizm 将文献中若干不同的强化学习算法分支(如学徒学习、变化、单一内在控制、约束和单一探索框架等)。