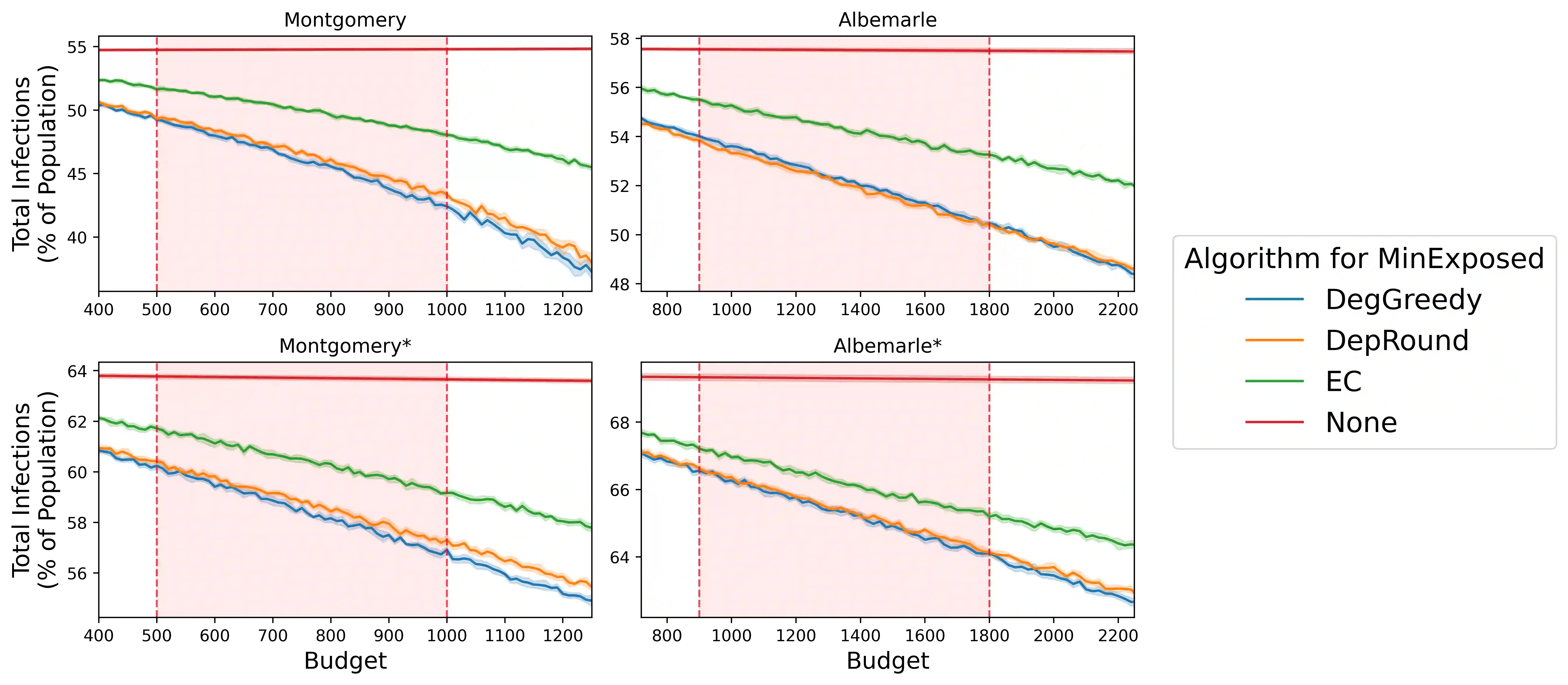
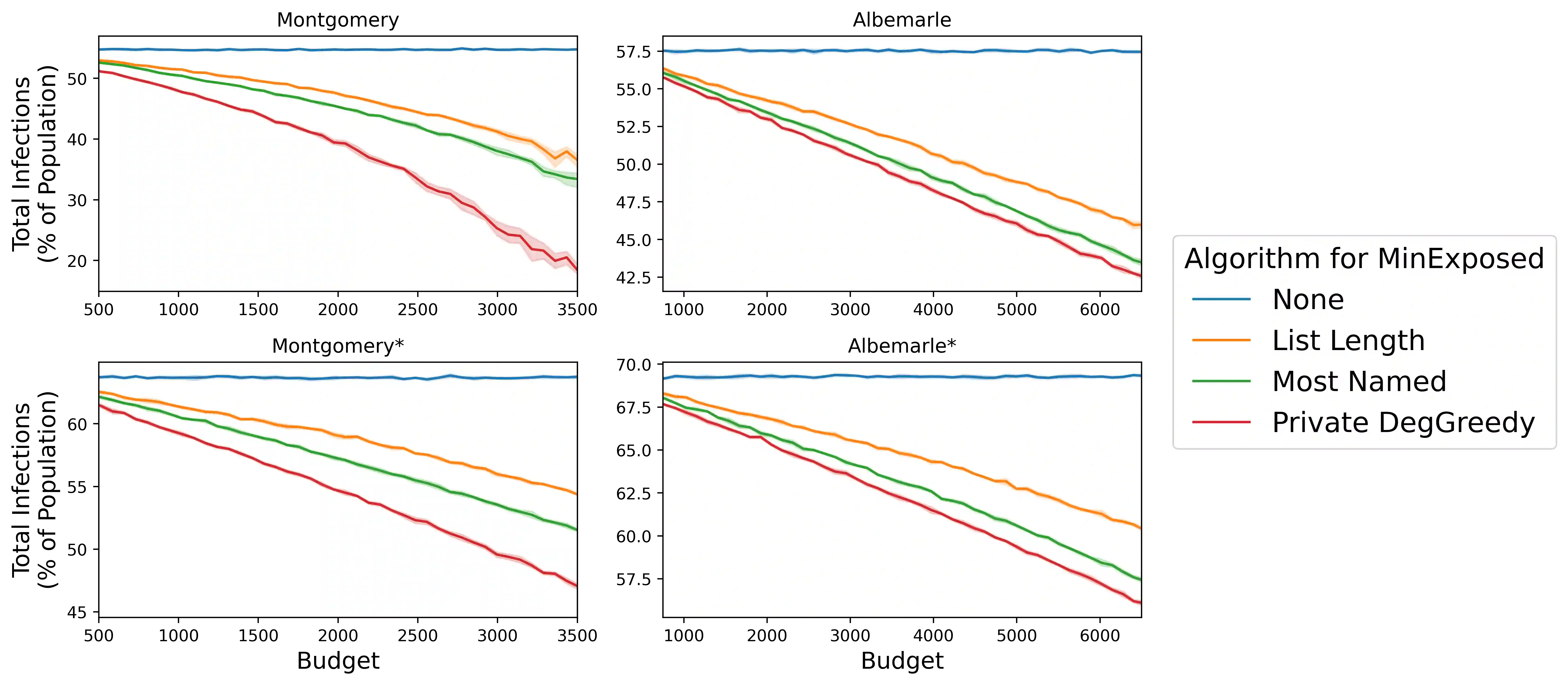
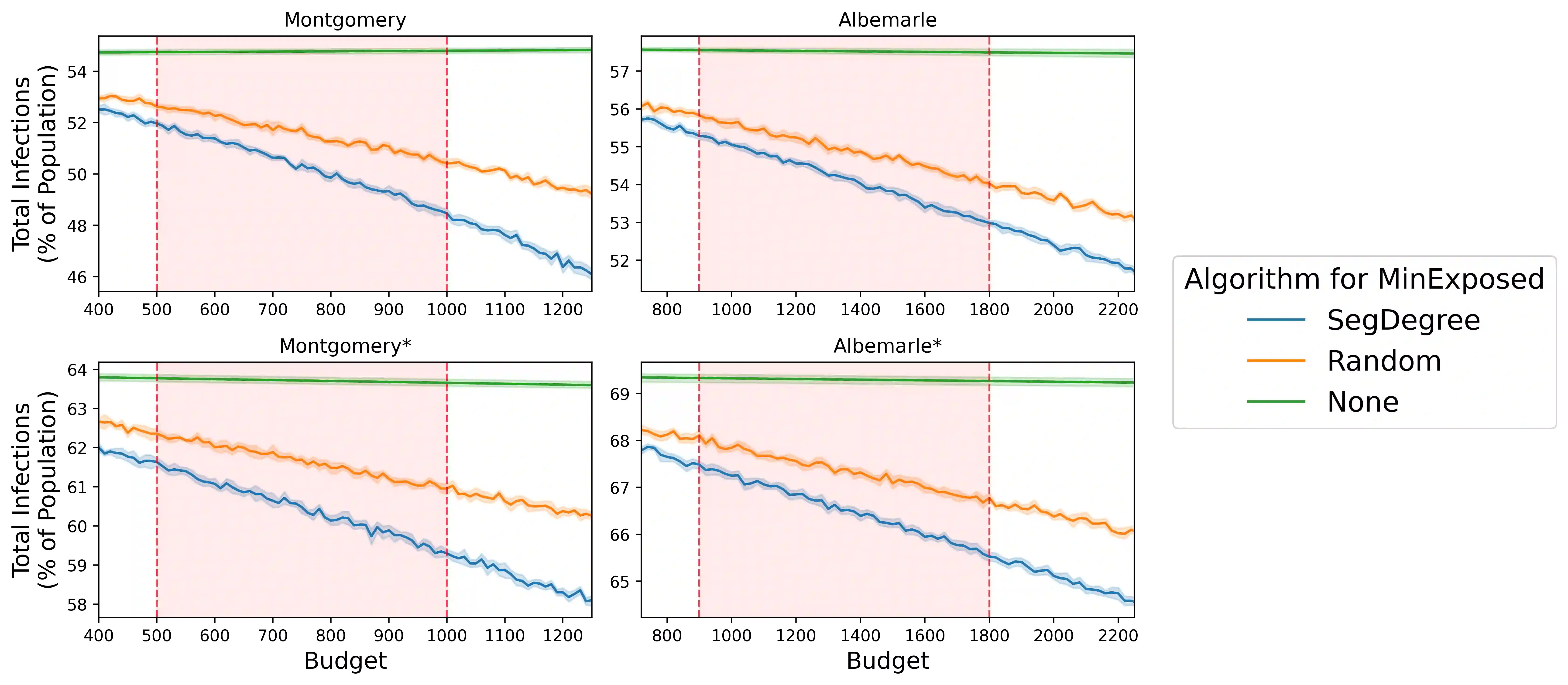
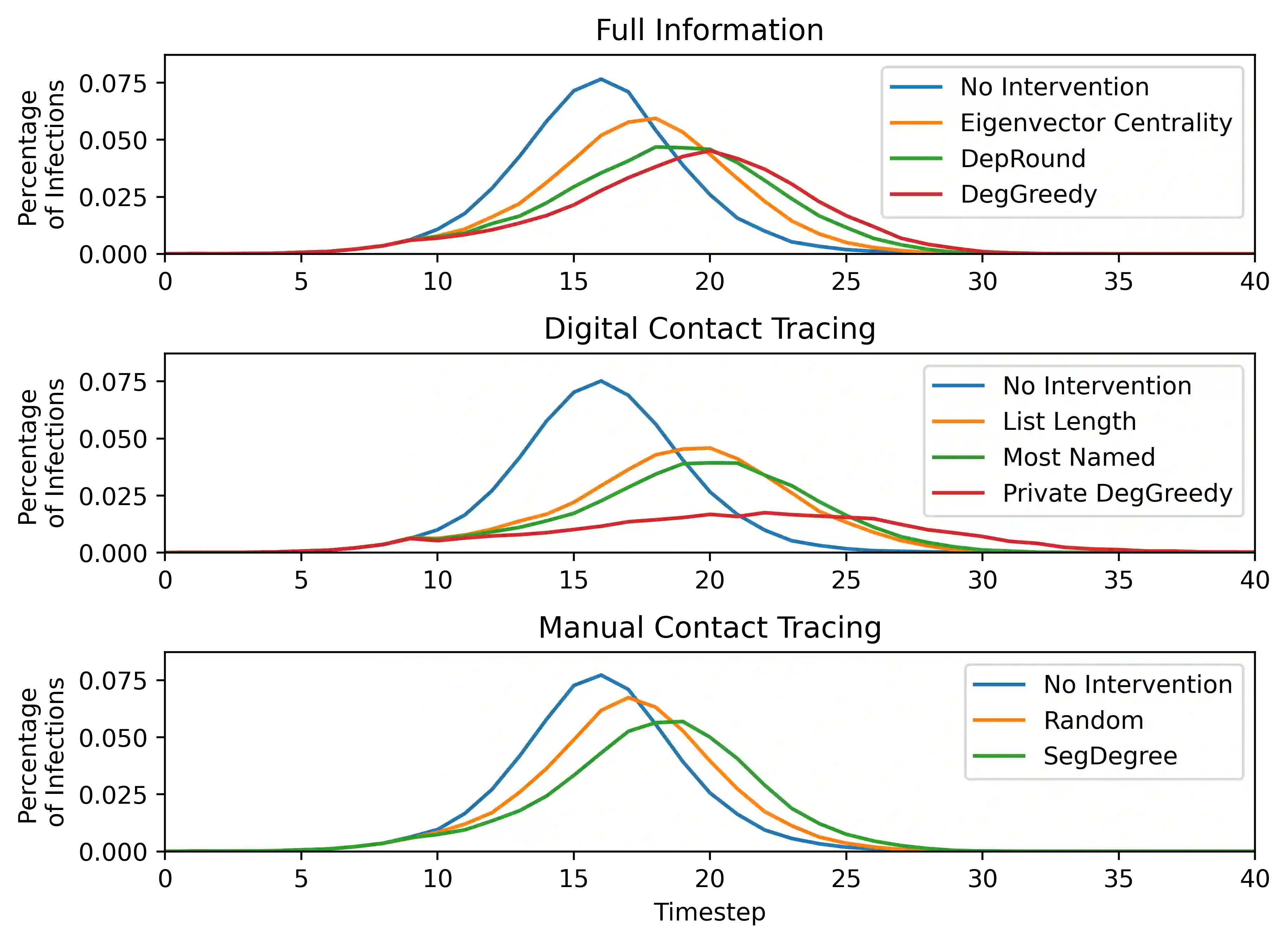
Efficient contact tracing and isolation is an effective strategy to control epidemics. It was used effectively during the Ebola epidemic and successfully implemented in several parts of the world during the ongoing COVID-19 pandemic. An important consideration in contact tracing is the budget on the number of individuals asked to quarantine -- the budget is limited for socioeconomic reasons. In this paper, we present a Markov Decision Process (MDP) framework to formulate the problem of using contact tracing to reduce the size of an outbreak while asking a limited number of people to quarantine. We formulate each step of the MDP as a combinatorial problem, MinExposed, which we demonstrate is NP-Hard; as a result, we develop an LP-based approximation algorithm. Though this algorithm directly solves MinExposed, it is often impractical in the real world due to information constraints. To this end, we develop a greedy approach based on insights from the analysis of the previous algorithm, which we show is more interpretable. A key feature of the greedy algorithm is that it does not need complete information of the underlying social contact network. This makes the heuristic implementable in practice and is an important consideration. Finally, we carry out experiments on simulations of the MDP run on real-world networks, and show how the algorithms can help in bending the epidemic curve while limiting the number of isolated individuals. Our experimental results demonstrate that the greedy algorithm and its variants are especially effective, robust, and practical in a variety of realistic scenarios, such as when the contact graph and specific transmission probabilities are not known. All code can be found in our GitHub repository: https://github.com/gzli929/ContactTracing.
翻译:高效的接触追踪和隔离是控制流行病的有效战略,在埃博拉疫情期间有效使用,并在目前COVID-19大流行期间在世界若干地区成功实施。联系追踪的一个重要考虑因素是要求隔离的人数预算 -- -- 预算因社会经济原因有限。在本文中,我们提出了一个Markov 决策程序框架,以制定使用接触追踪来减少爆发规模的问题,同时要求数量有限的人进行隔离。我们把MDP的每一个步骤都设计成一个组合问题,即MinExposed,我们展示的是NP-Hard;结果,我们开发了一个基于LP的近似算法。尽管这种算法直接解决了MinExplosed,但由于信息限制,在现实世界中往往不切实际。我们根据对先前算法的分析来制定一种贪婪的方法,我们所展示的是,我们所找到的社会接触网络的精细细度并不需要完整的信息。这使我们的直观执行规则,因此,我们开发一个基于LP-P的近算法,这是一个重要的考量。最后,我们通过这个算法在现实的模型中进行我们所知道的路径的路径上的路径上的路径,我们是如何在模拟中可以用来显示我们所知道的轨道上的路径上的路径上的路径上的路径上的路径变压。我们是如何在模拟中可以帮助。