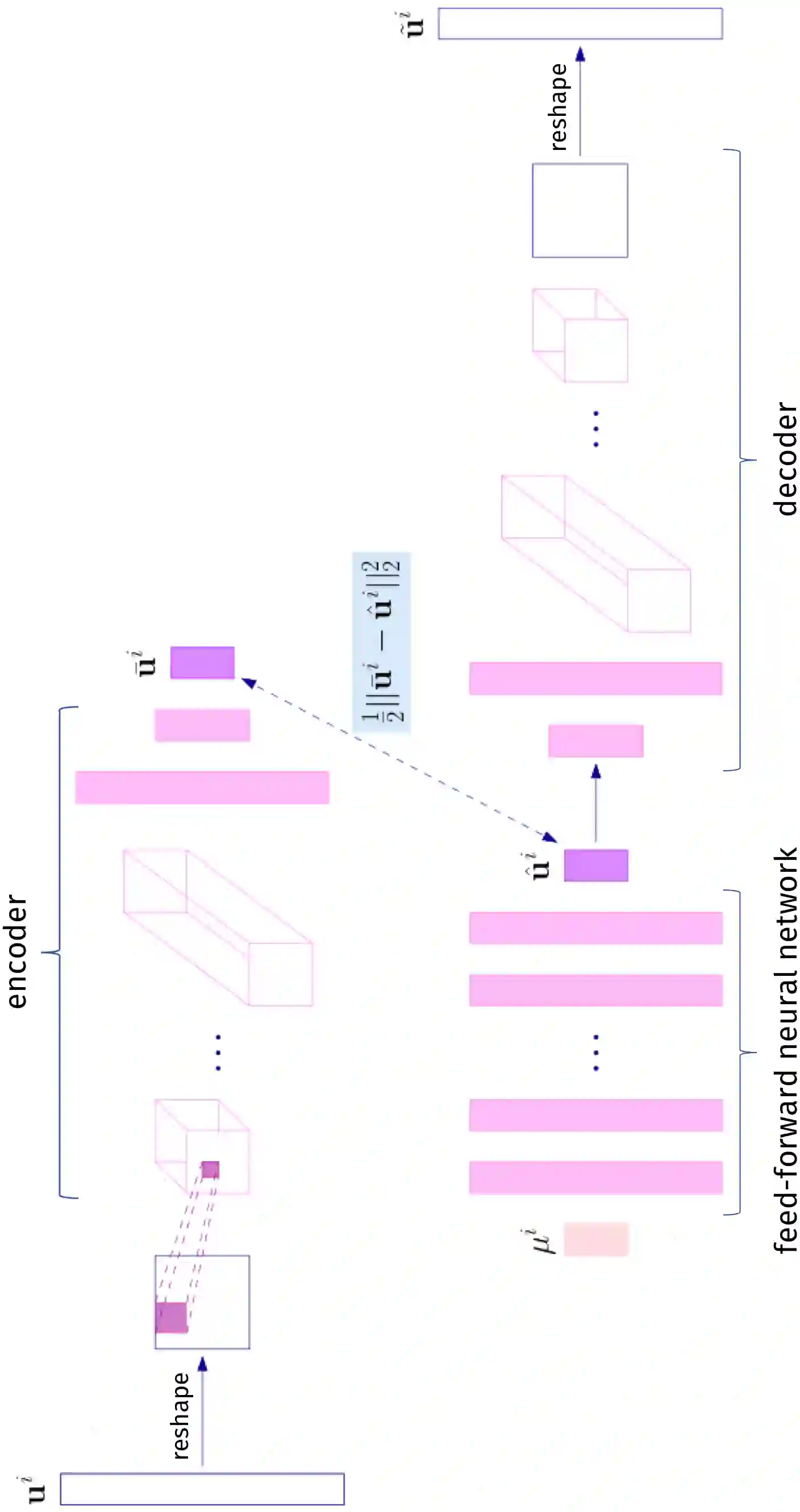
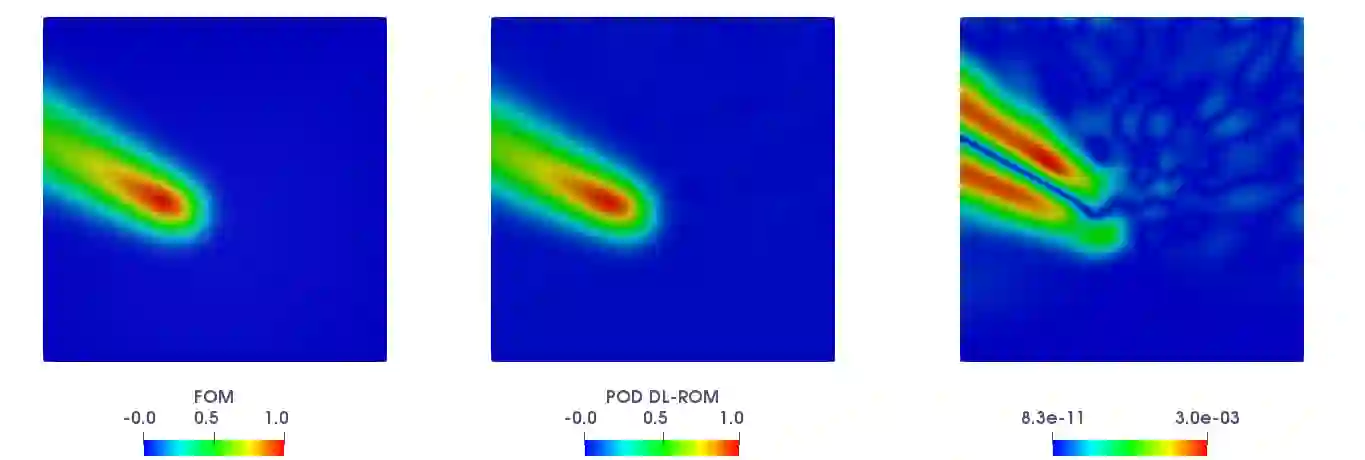
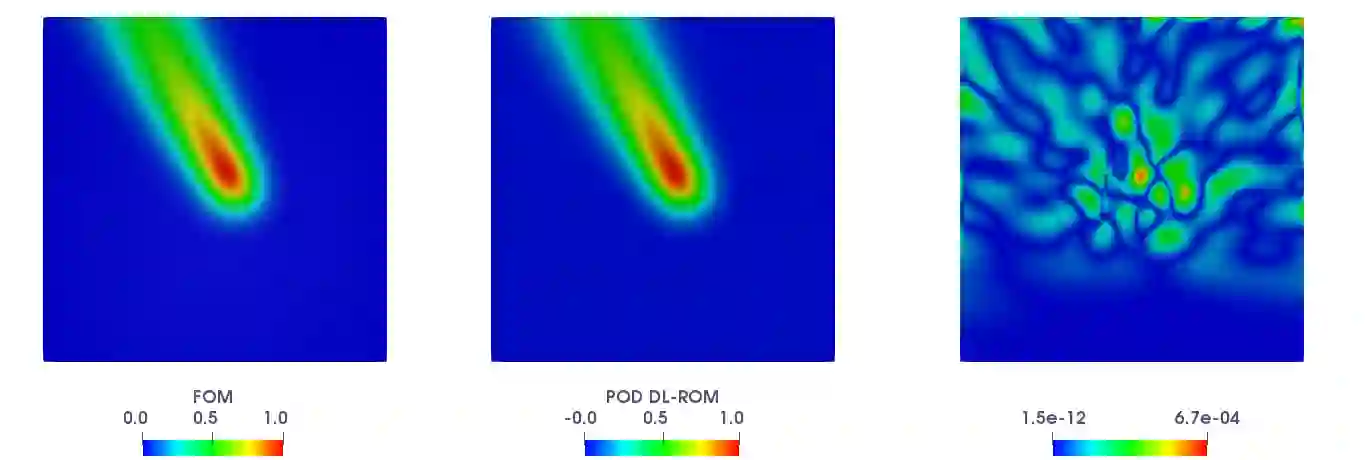
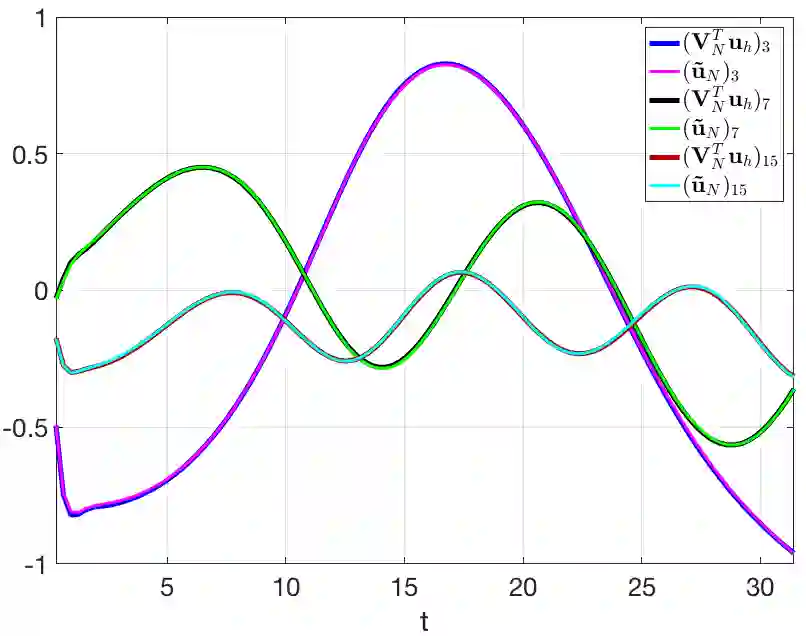
Deep learning-based reduced order models (DL-ROMs) have been recently proposed to overcome common limitations shared by conventional reduced order models (ROMs) - built, e.g., through proper orthogonal decomposition (POD) - when applied to nonlinear time-dependent parametrized partial differential equations (PDEs). These might be related to (i) the need to deal with projections onto high dimensional linear approximating trial manifolds, (ii) expensive hyper-reduction strategies, or (iii) the intrinsic difficulty to handle physical complexity with a linear superimposition of modes. All these aspects are avoided when employing DL-ROMs, which learn in a non-intrusive way both the nonlinear trial manifold and the reduced dynamics, by relying on deep (e.g., feedforward, convolutional, autoencoder) neural networks. Although extremely efficient at testing time, when evaluating the PDE solution for any new testing-parameter instance, DL-ROMs require an expensive training stage, because of the extremely large number of network parameters to be estimated. In this paper we propose a possible way to avoid an expensive training stage of DL-ROMs, by (i) performing a prior dimensionality reduction through POD, and (ii) relying on a multi-fidelity pretraining stage, where different physical models can be efficiently combined. The proposed POD-DL-ROM is tested on several (both scalar and vector, linear and nonlinear) time-dependent parametrized PDEs (such as, e.g., linear advection-diffusion-reaction, nonlinear diffusion-reaction, nonlinear elastodynamics, and Navier-Stokes equations) to show the generality of this approach and its remarkable computational savings.
翻译:最近提议了深层学习式降序模型(DL-ROM),以克服常规降序模型(ROM)所共有的共同限制(DL-ROM) -- -- 建造的常规降序模型(ROM)所共有的共同限制,例如,当应用到非线性时间依赖的超光化部分偏差方程式(PDEs)时,这些模型可能与以下因素有关:(一) 需要处理向高维线性近线性试验管(DL-ROM)的预测,(二) 昂贵的超光度战略,或(三) 使用直线性超模(ROM)处理物理复杂性的内在困难。当使用DL-ROM(S-ROM)时,所有这些方面都避免了,以非侵入性的方式学习非线性线性试验的多光线性线性分解(Pl-ROD-OD-G-S-Procial-Procial-deal-deal-deal-deal-deal-deal-deal-deal-demodeal-al-de-deal-deal-deal-al-demodeal-de-de-al-de-de-de-de-de-deal-deal-deal-deal-lational-deal-deal-deal-al-de-de-al-al-al-al-al-de-de-de-de-de-lational-l),我们表),我们提出一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的、一个可能的不透明的不透明的、一个可能的、一个在前的、一个不规则-ODDDDDDDDD-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-de-s-de-de-de-mod-mod-l-de-de-de-de-de-de-de-de-