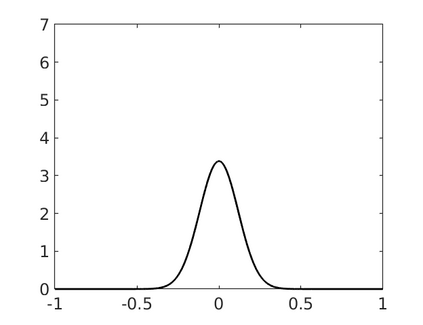
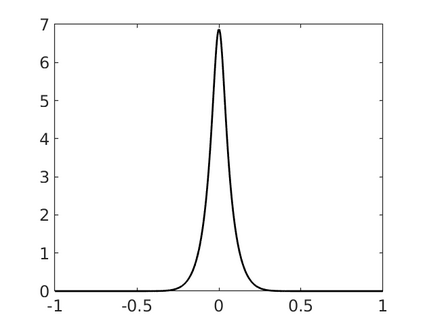
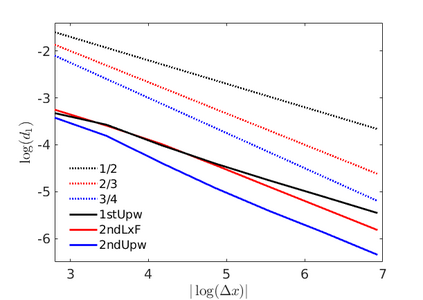
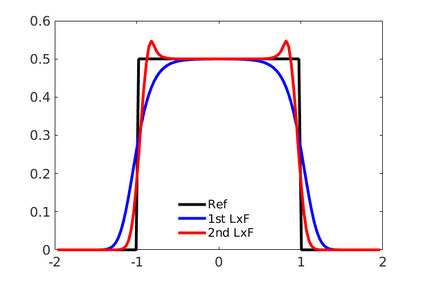
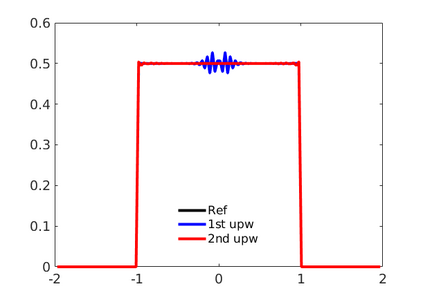
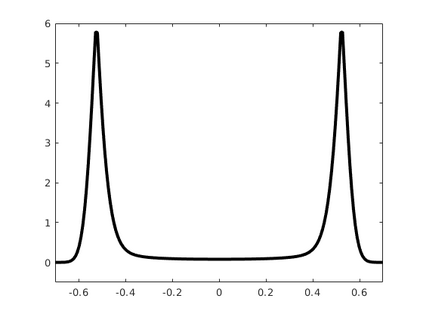
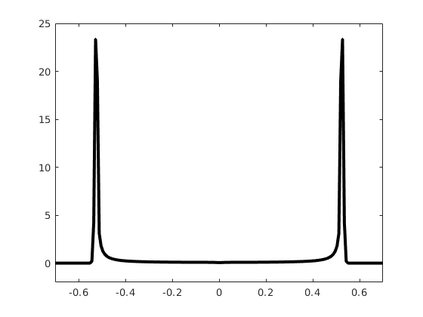
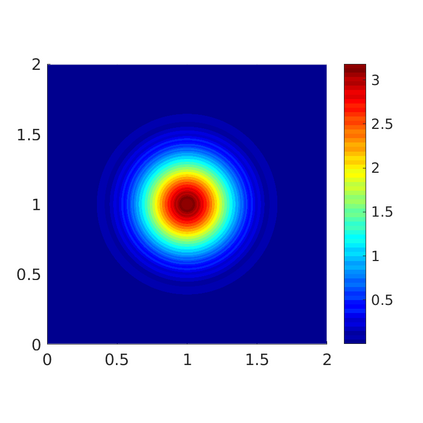
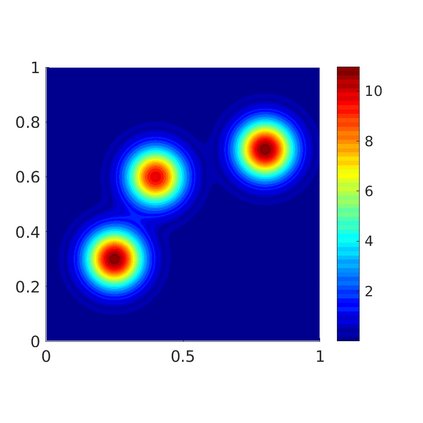
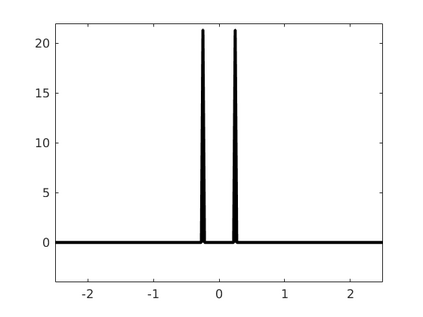
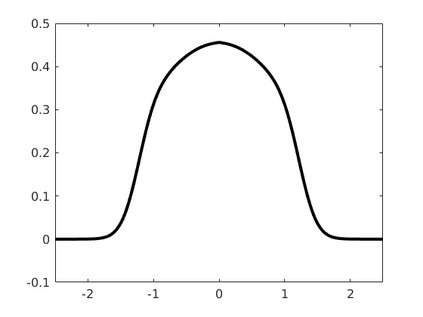
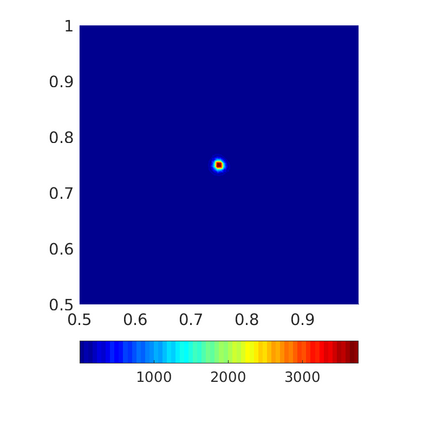
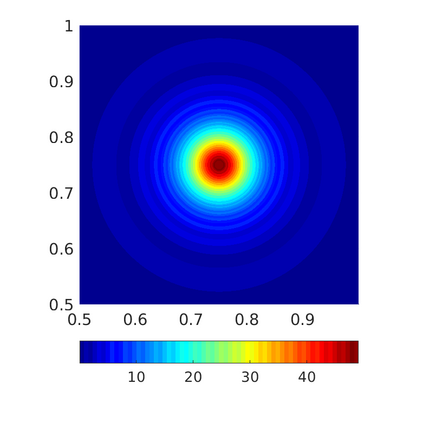
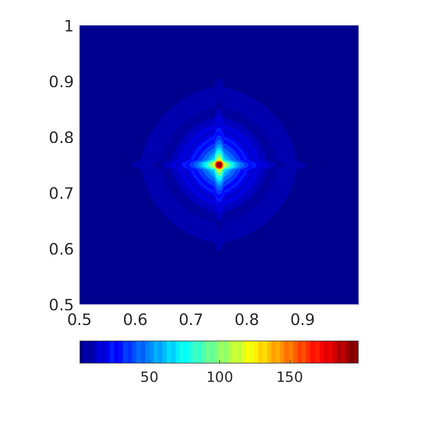
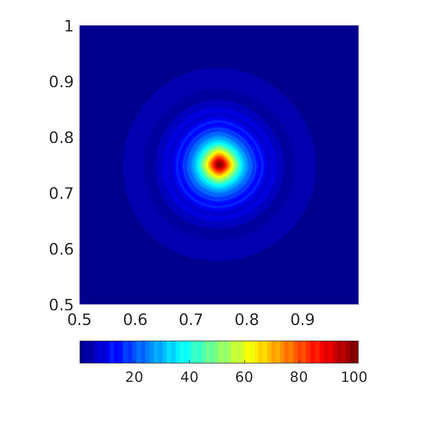
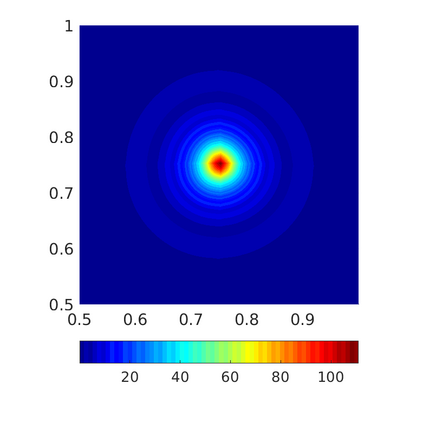
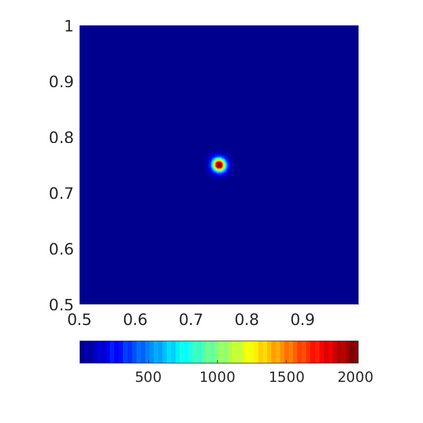
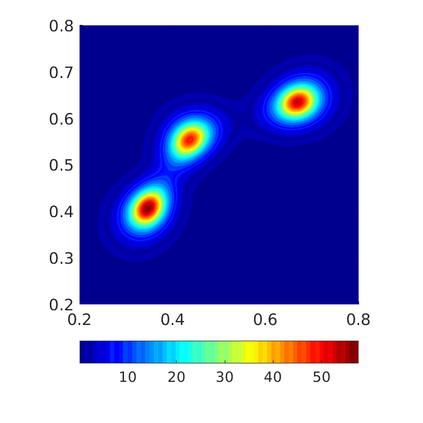
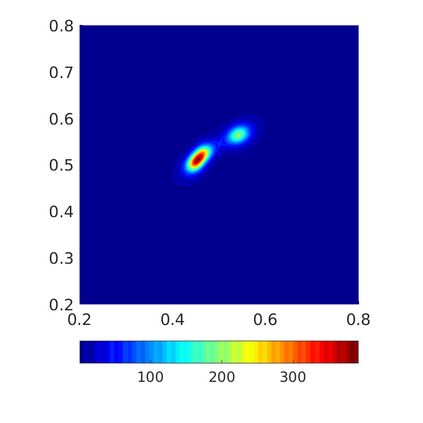
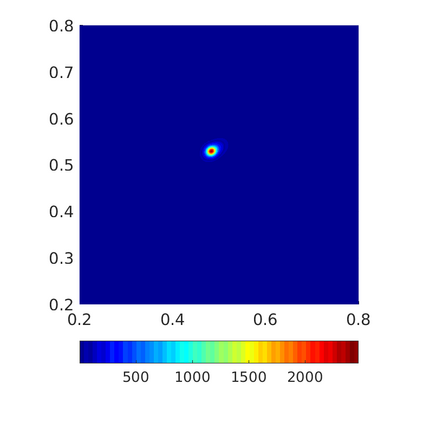
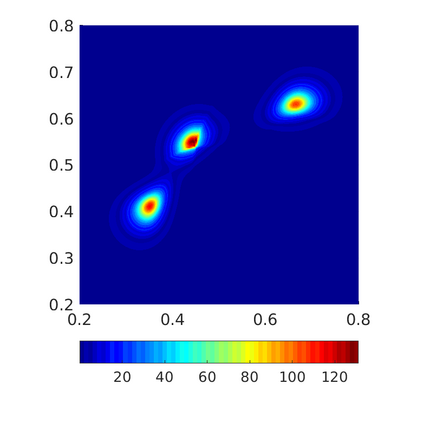
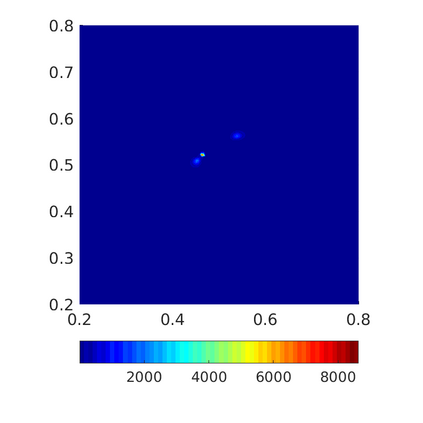
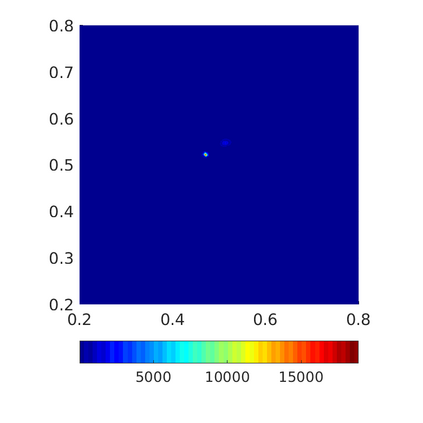
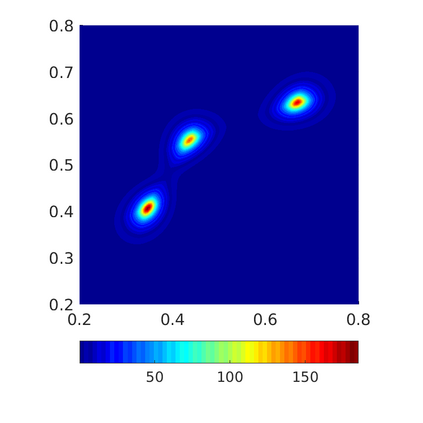
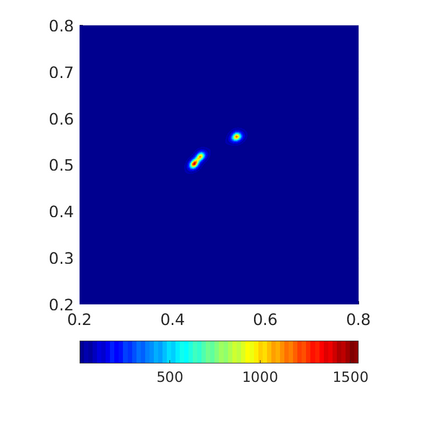
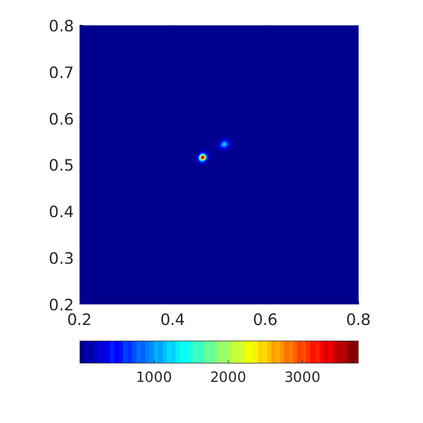
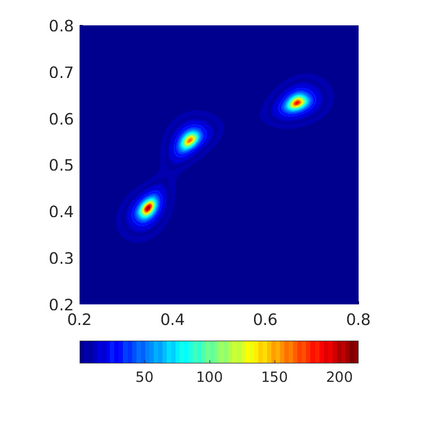
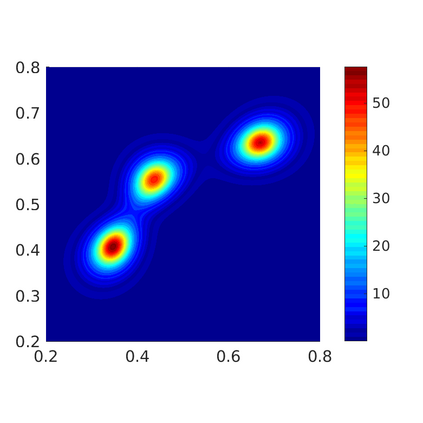
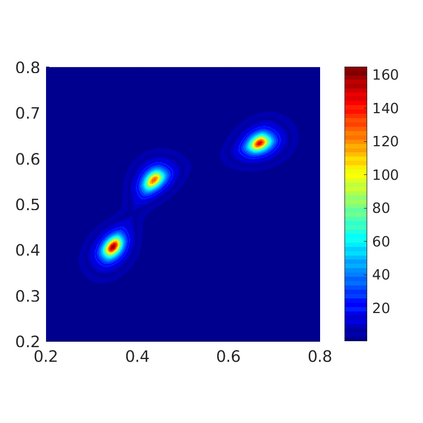
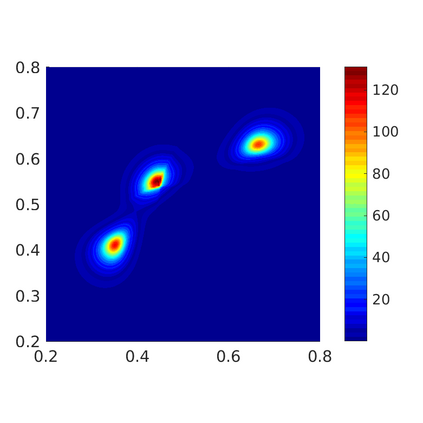
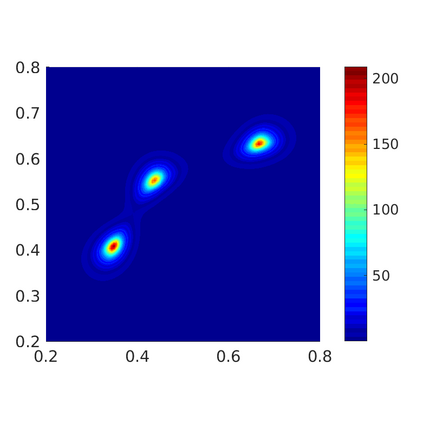
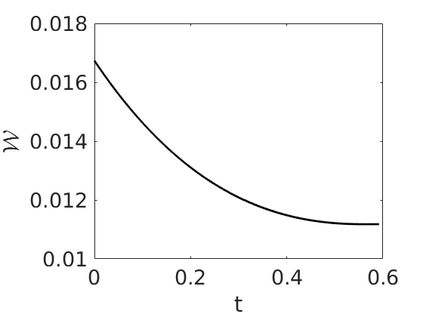
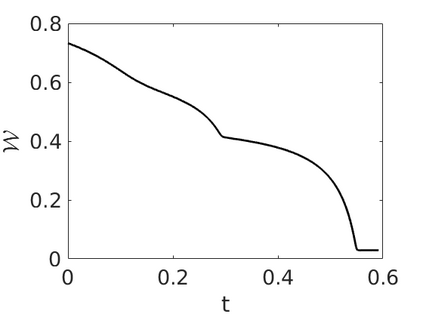
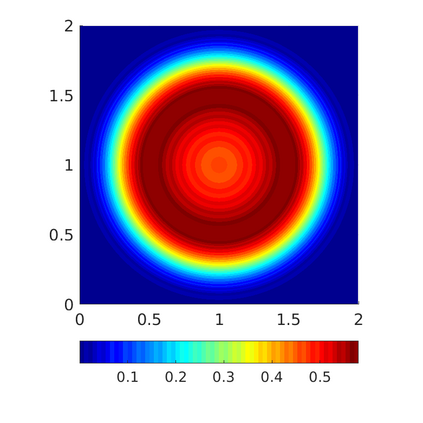
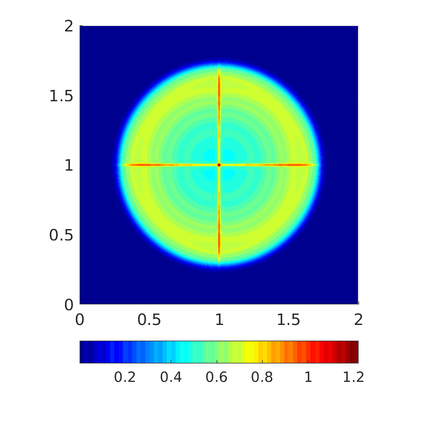
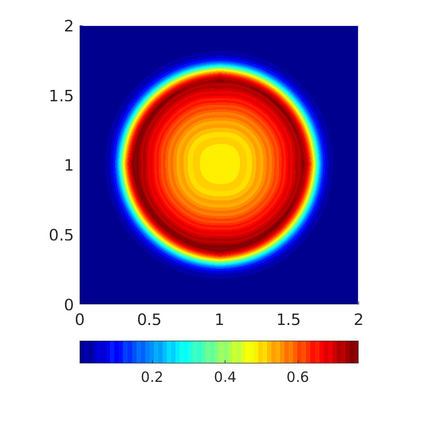
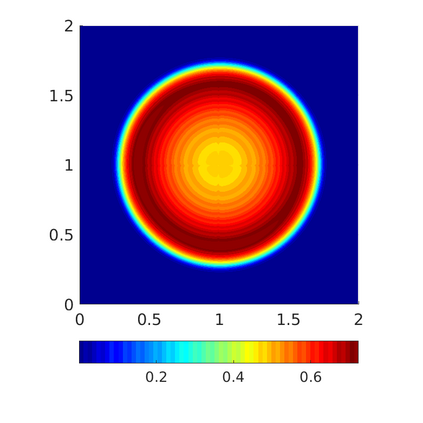
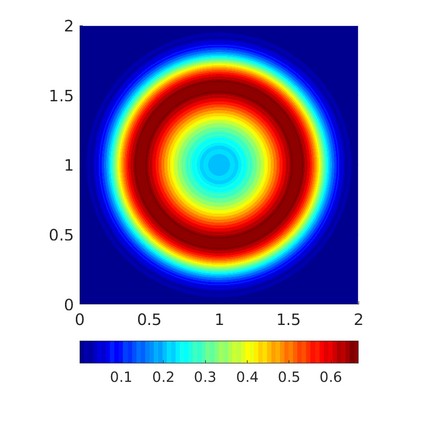
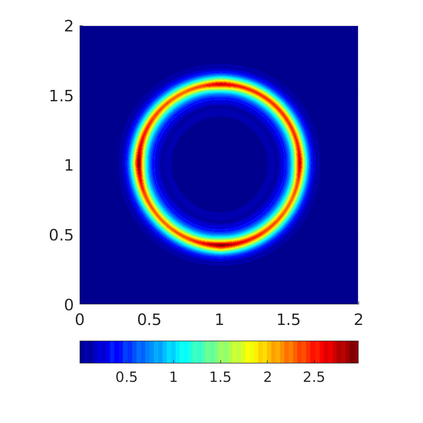
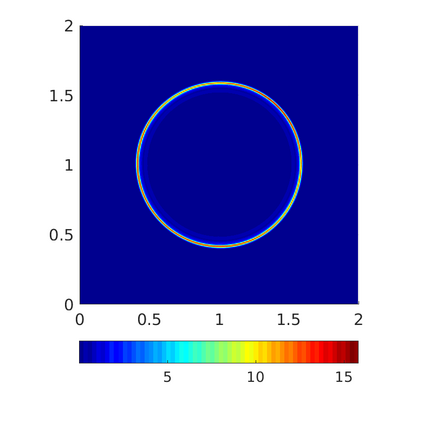
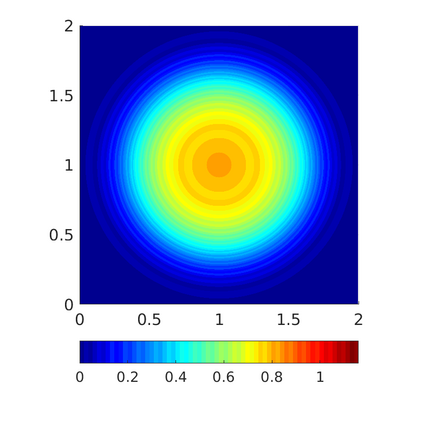
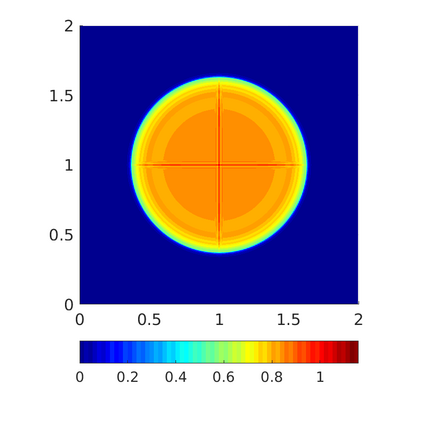
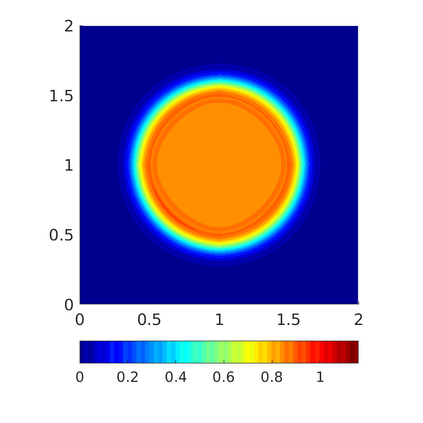
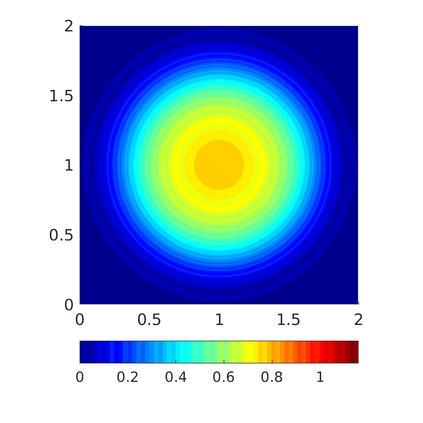
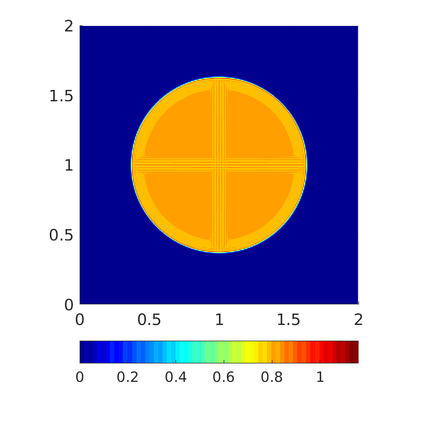
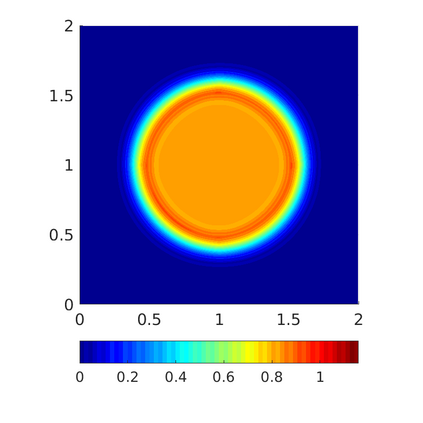
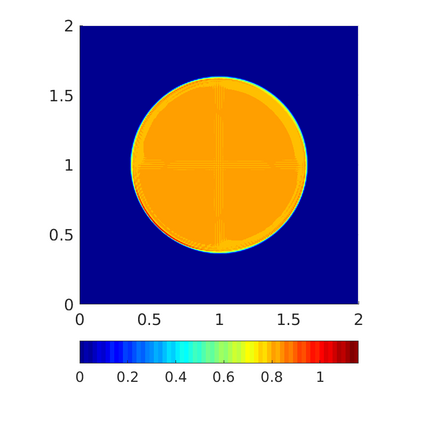
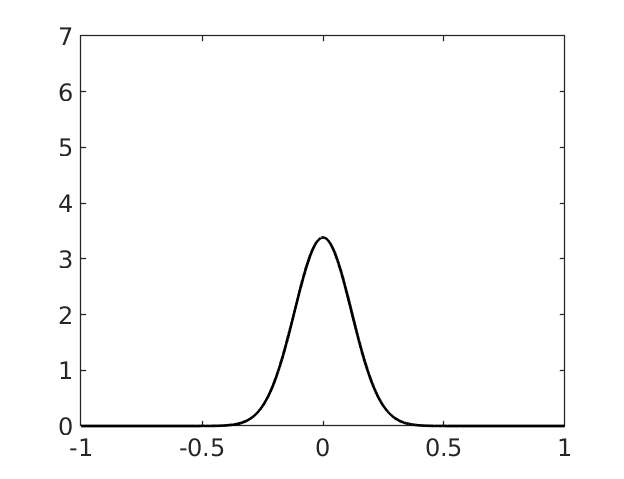
Inspired by so-called TVD limiter-based second-order schemes for hyperbolic conservation laws, we develop a second-order accurate numerical method for multi-dimensional aggregation equations. The method allows for simulations to be continued after the first blow-up time of the solution. In the case of symmetric, lambda-convex potentials with a possible Lipschitz singularity at the origin we prove that the method converges in the Monge--Kantorovich distance towards the unique gradient flow solution. Several numerical experiments are presented to validate the second-order convergence rate and to explore the performance of the scheme.
翻译:在所谓的基于TVD限制的双曲保护法第二序列计划的启发下,我们为多维聚合方程式开发了第二阶精确数字方法,该方法允许在解决方案第一次爆炸后继续进行模拟。在对称的情况下,用Lipschitz的独一性,我们证明该方法在蒙盖-坎托罗维奇距离与独特的梯度流解方法相融合。为了验证第二阶汇合率和探索该方法的性能,我们提出了数项实验。
相关内容
Source: Apple - iOS 8