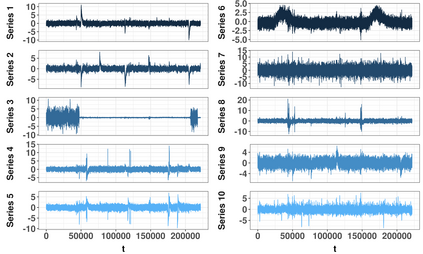
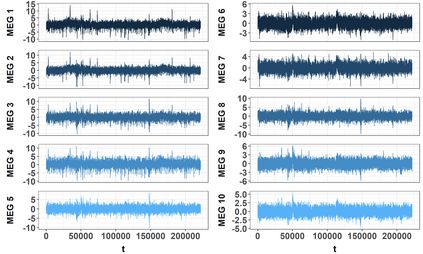
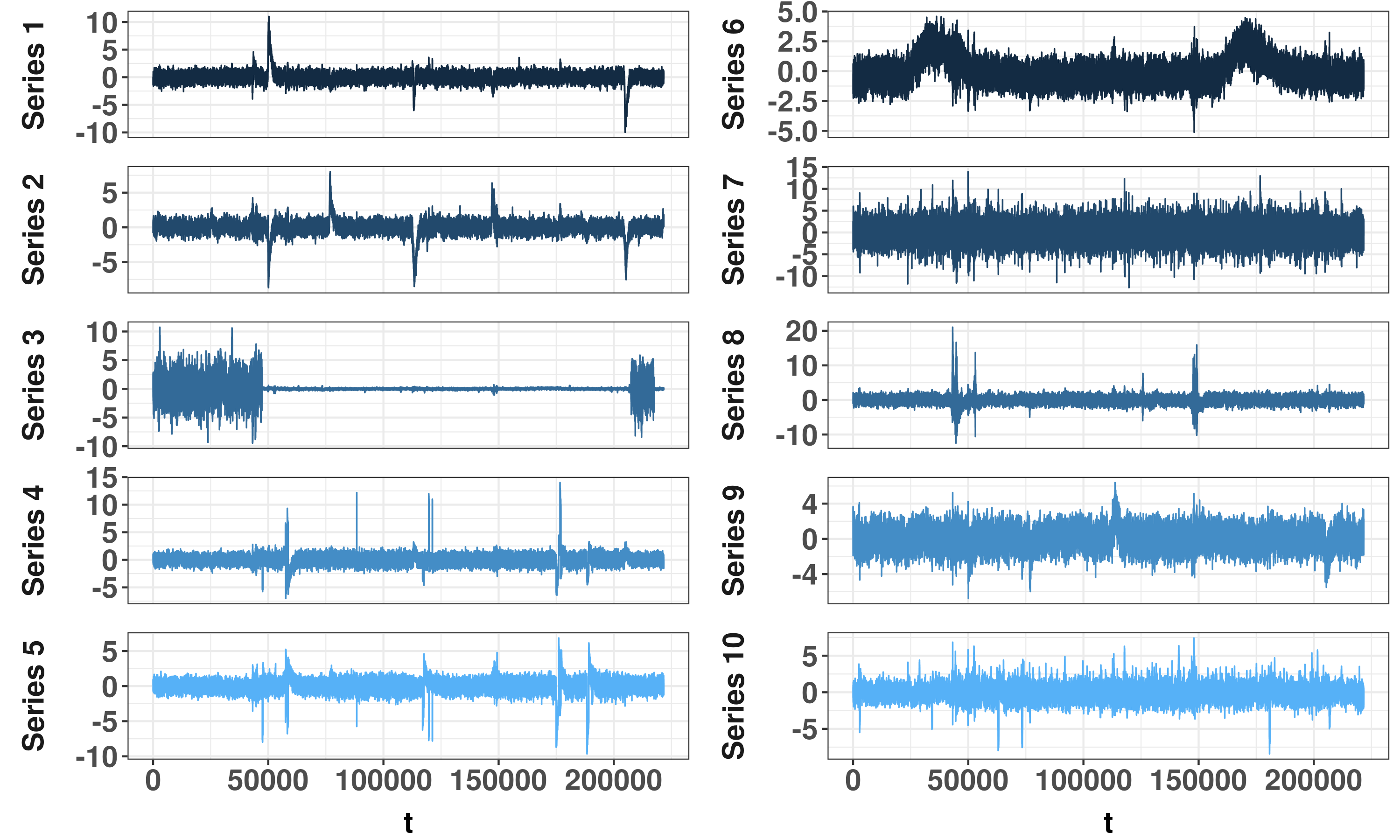
In stationary subspace analysis (SSA) one assumes that the observable p-variate time series is a linear mixture of a k-variate nonstationary time series and a (p-k)-variate stationary time series. The aim is then to estimate the unmixing matrix which transforms the observed multivariate time series onto stationary and nonstationary components. In the classical approach multivariate data are projected onto stationary and nonstationary subspaces by minimizing a Kullback-Leibler divergence between Gaussian distributions, and the method only detects nonstationarities in the first two moments. In this paper we consider SSA in a more general multivariate time series setting and propose SSA methods which are able to detect nonstationarities in mean, variance and autocorrelation, or in all of them. Simulation studies illustrate the performances of proposed methods, and it is shown that especially the method that detects all three types of nonstationarities performs well in various time series settings. The paper is concluded with an illustrative example.
翻译:在静止子空间分析(SSA)中,假设可观测的p变量时间序列是一个 k- 变量非静止时间序列和 (p-k) 变量固定时间序列的线性混合物,然后目的是估计将观测到的多变量时间序列转换为固定和非静止组成部分的未混合矩阵。在古典方法中,多变量数据投射到固定和非静止的子空间,办法是尽量减少高山分布之间的Kullback- Leiber差异,而该方法仅在头两个时刻探测非静止。在本文件中,我们在一个比较一般的多变量时间序列设置中考虑SSA,并提出能够探测到平均值、差异和自动或所有这些组成部分的非静止现象的SSA方法。模拟研究说明了拟议方法的性能,并表明,特别是检测所有三种非静止类型的方法的方法在不同时间序列环境中表现良好。本文以示例形式结尾。