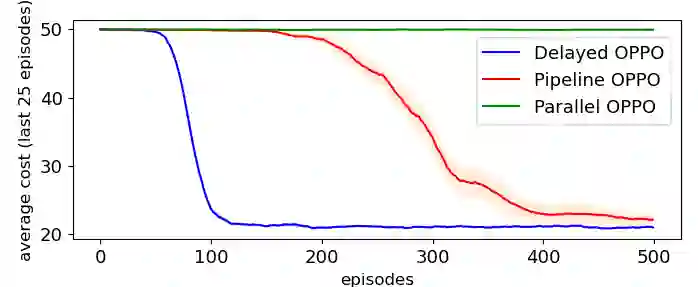
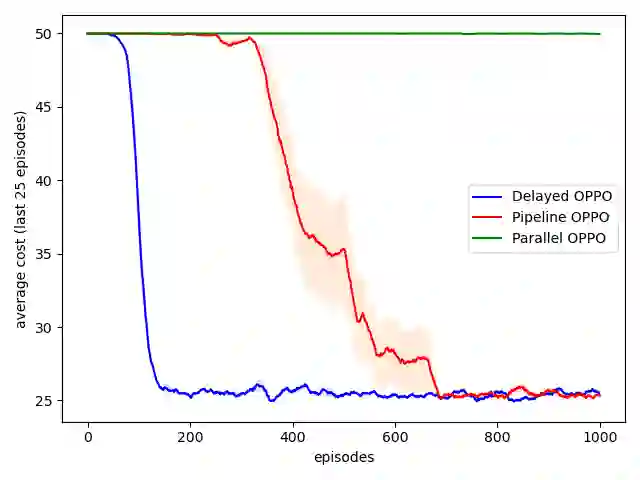
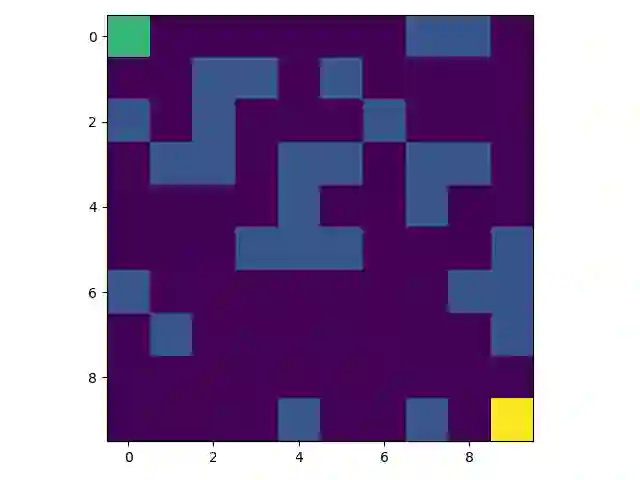
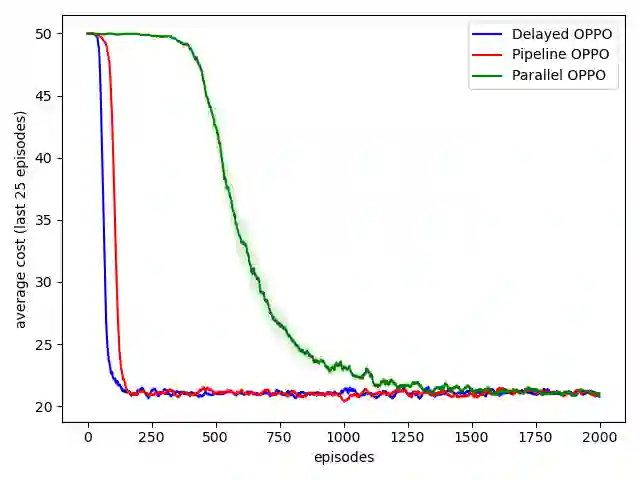
Reinforcement learning typically assumes that agents observe feedback for their actions immediately, but in many real-world applications (like recommendation systems) feedback is observed in delay. This paper studies online learning in episodic Markov decision processes (MDPs) with unknown transitions, adversarially changing costs and unrestricted delayed feedback. That is, the costs and trajectory of episode $k$ are revealed to the learner only in the end of episode $k + d^k$, where the delays $d^k$ are neither identical nor bounded, and are chosen by an oblivious adversary. We present novel algorithms based on policy optimization that achieve near-optimal high-probability regret of $\sqrt{K + D}$ under full-information feedback, where $K$ is the number of episodes and $D = \sum_{k} d^k$ is the total delay. Under bandit feedback, we prove similar $\sqrt{K + D}$ regret assuming the costs are stochastic, and $(K + D)^{2/3}$ regret in the general case. We are the first to consider regret minimization in the important setting of MDPs with delayed feedback.
翻译:强化学习通常假定代理商立即观察对其行动的反馈,但许多实际应用(如建议系统)的反馈却被推迟。本文研究在未为人知的过渡、对抗性变化成本和无限制延迟反馈的Supsodic Markov决策程序中在线学习,也就是说,在 " $ + d'k " 的插曲结束时,才向学习者披露k美元的费用和轨迹。在 " $ +'d'k " 的插曲中,延迟的美元既不相同,也没有约束,而是被一个模糊的对手所选择。我们根据政策优化提出新的算法,在 " 完整信息反馈 " 下,实现接近最佳高概率的美元+D'的遗憾,而 " $ " 是事件的数量,而 " $='='sum'k'd'k'd'k " 是全部延迟。在 " 的插曲中,我们证明类似的 $\qrt{k{K+ D}是被一个不知名的对手选择的。我们在一般的反馈中,我们首先认为成本是随机,而$ (K+D]2]/3美元与 " 令人遗憾。