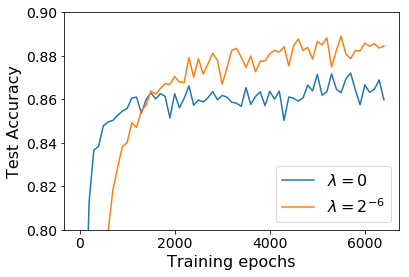
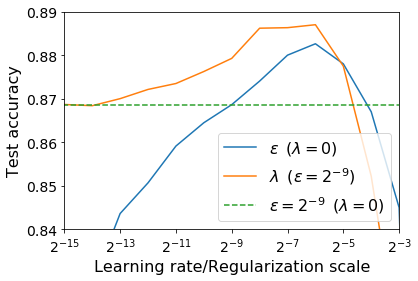
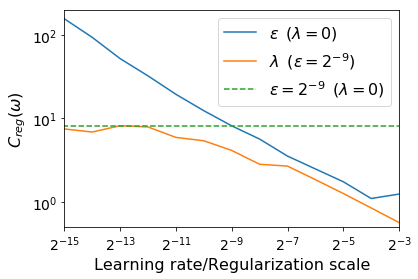
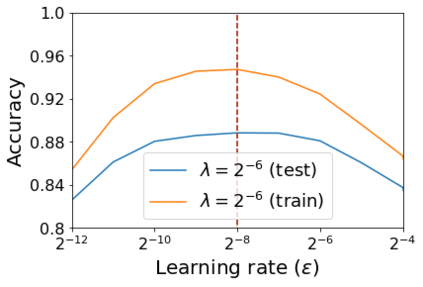
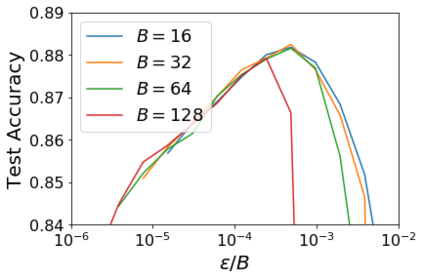
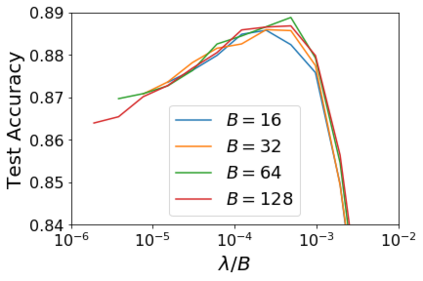
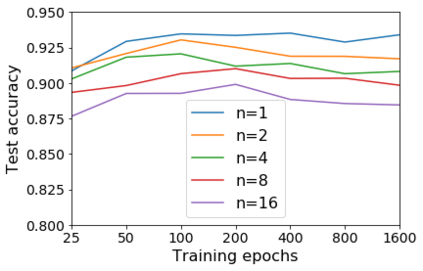
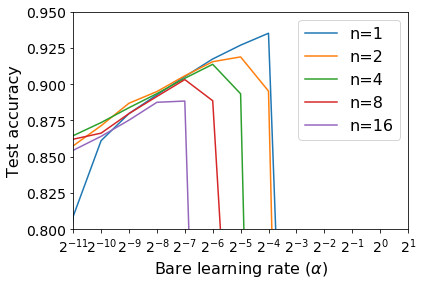
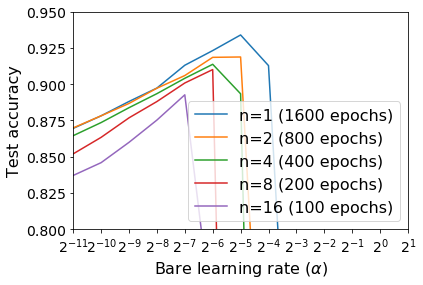
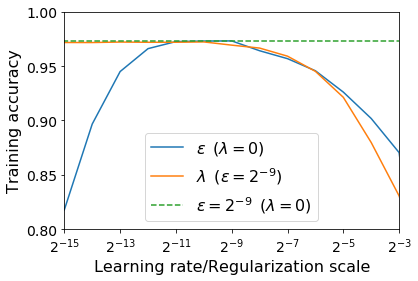
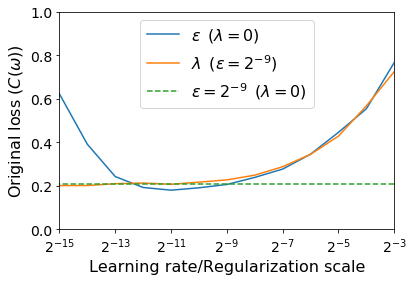
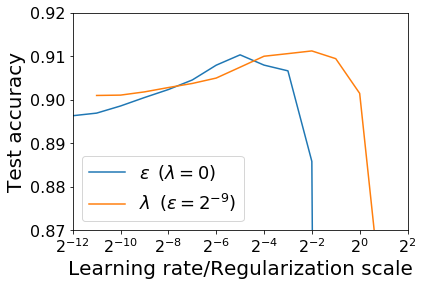
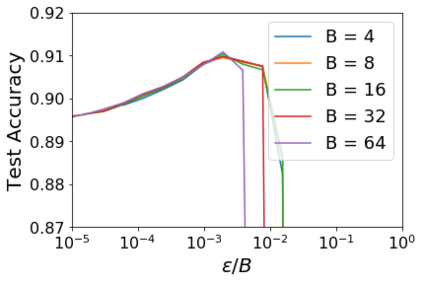
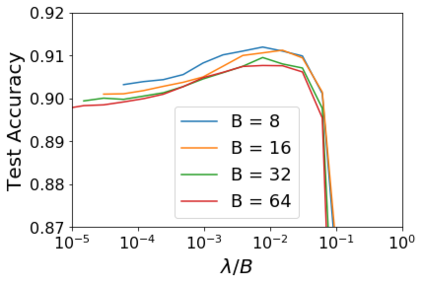
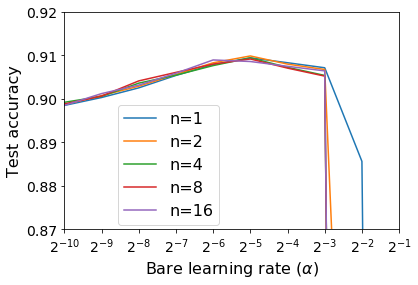
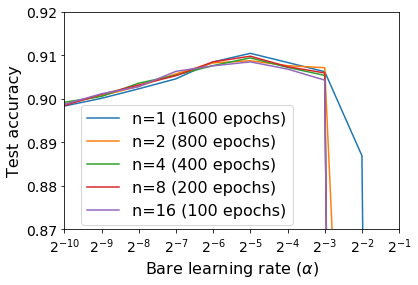
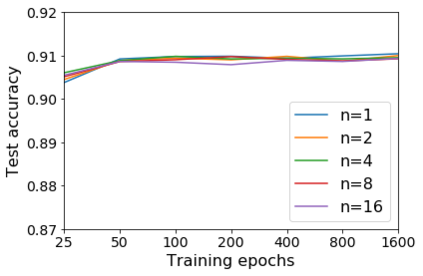
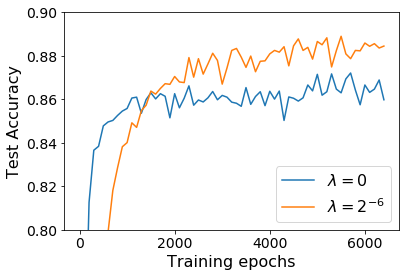
For infinitesimal learning rates, stochastic gradient descent (SGD) follows the path of gradient flow on the full batch loss function. However moderately large learning rates can achieve higher test accuracies, and this generalization benefit is not explained by convergence bounds, since the learning rate which maximizes test accuracy is often larger than the learning rate which minimizes training loss. To interpret this phenomenon we prove that for SGD with random shuffling, the mean SGD iterate also stays close to the path of gradient flow if the learning rate is small and finite, but on a modified loss. This modified loss is composed of the original loss function and an implicit regularizer, which penalizes the norms of the minibatch gradients. Under mild assumptions, when the batch size is small the scale of the implicit regularization term is proportional to the ratio of the learning rate to the batch size. We verify empirically that explicitly including the implicit regularizer in the loss can enhance the test accuracy when the learning rate is small.
翻译:对于极小的学习率,微小的梯度梯度下降(SGD)沿着全批损失函数的梯度流路径。然而,中等大的学习率可以达到较高的测试加速度,而这种一般化的好处并不是由趋同界限解释的,因为最大限度地提高测试准确度的学习率往往大于最大限度地降低培训损失的学习率。为了解释这种现象,我们证明,对于随机调整的SGD来说,如果学习率小而有限,平均的SGD 偏移率也接近于梯度流。这一修改的损失是由原来的损失函数和隐含的调节器构成的,它惩罚了微型批量梯度的规范。根据轻度假设,当批量规模小时,隐含的正规化术语的规模与学习率与批量规模的比例成比例成比例成比例成正比。我们从经验上核实,如果将隐含的正值的正值纳入损失中,则可以提高学习率时的测试准确度。