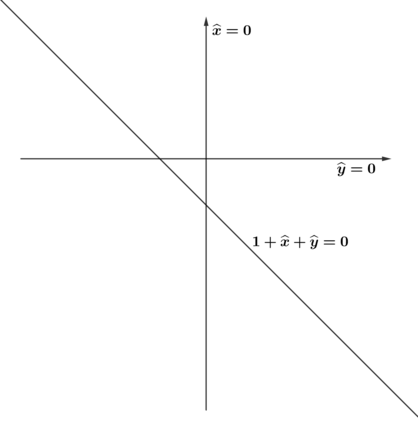
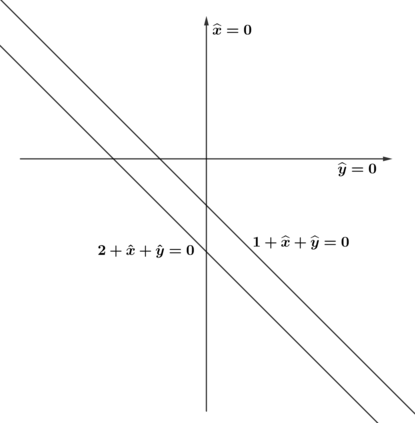
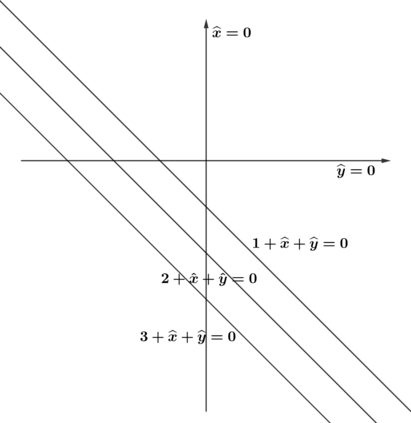
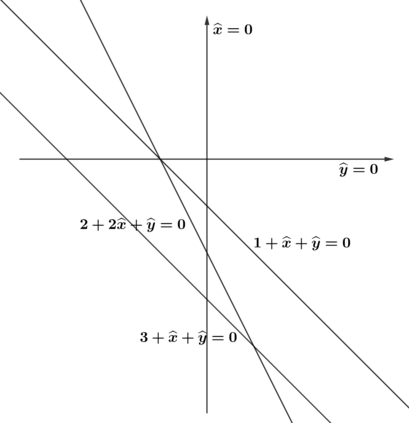
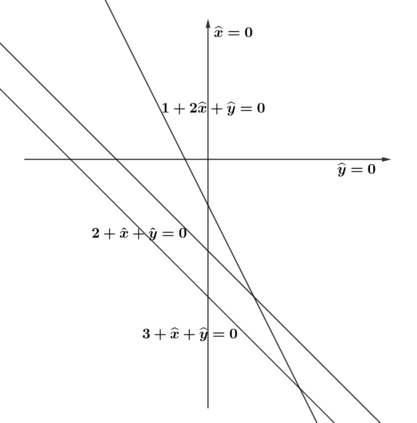
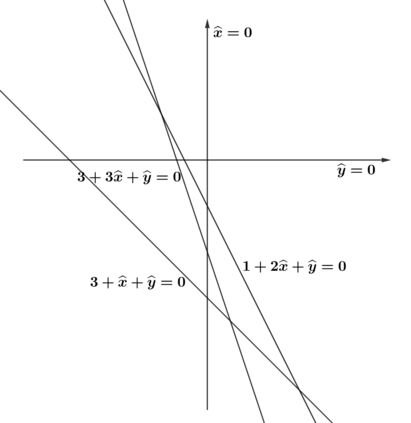
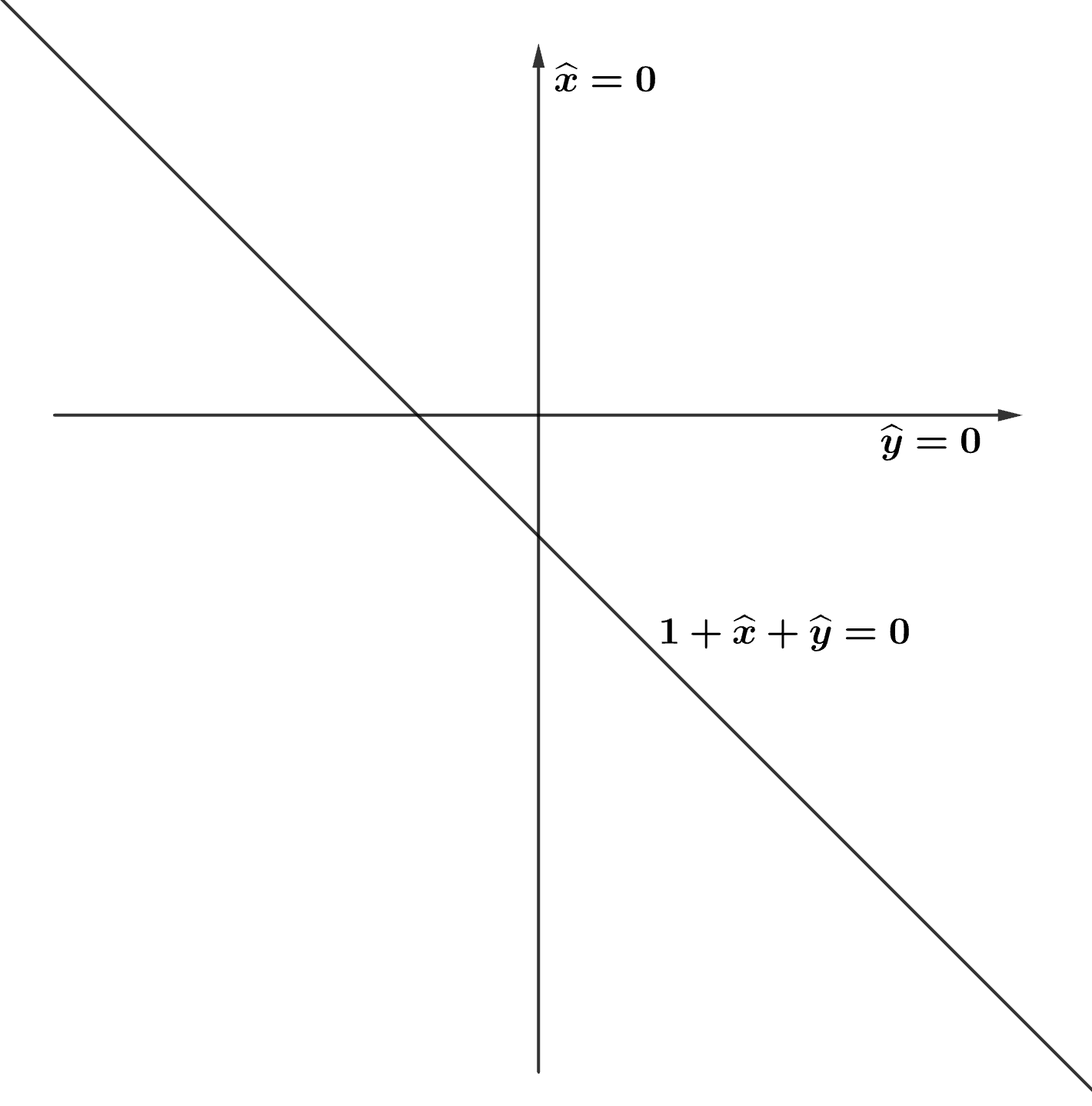
We study the maximum likelihood (ML) degree of discrete exponential independence models and models defined by the second hypersimplex. For models with two independent variables, we show that the ML degree is an invariant of a matroid associated to the model. We use this description to explore ML degrees via hyperplane arrangements. For independence models with more variables, we investigate the connection between the vanishing of factors of its principal $A$-determinant and its ML degree. Similarly, for models defined by the second hypersimplex, we determine its principal $A$-determinant and give computational evidence towards a conjectured lower bound of its ML degree.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2024年3月22日
Arxiv
0+阅读 · 2024年3月22日