On the bilateral preconditioning for a L2-type all-at-once system arising from time-space fractional Bloch-Torrey equations

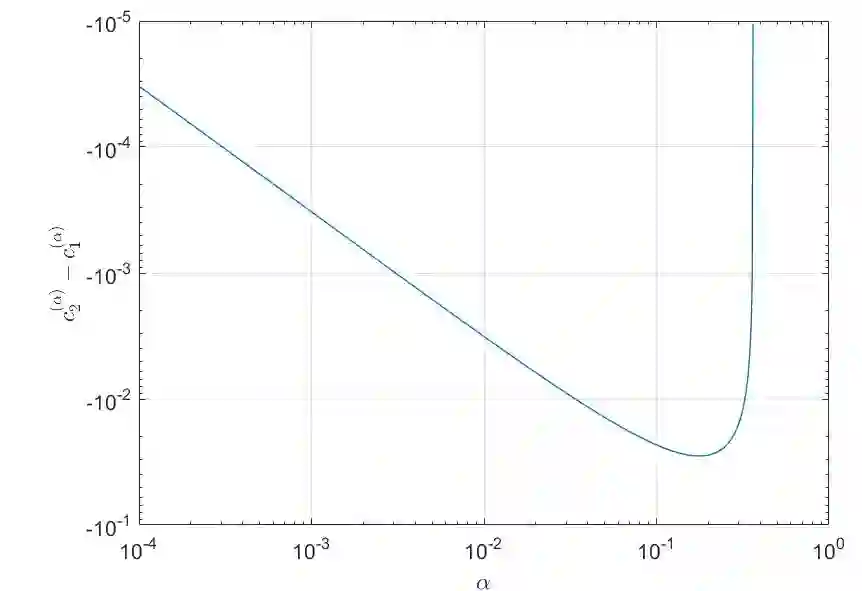
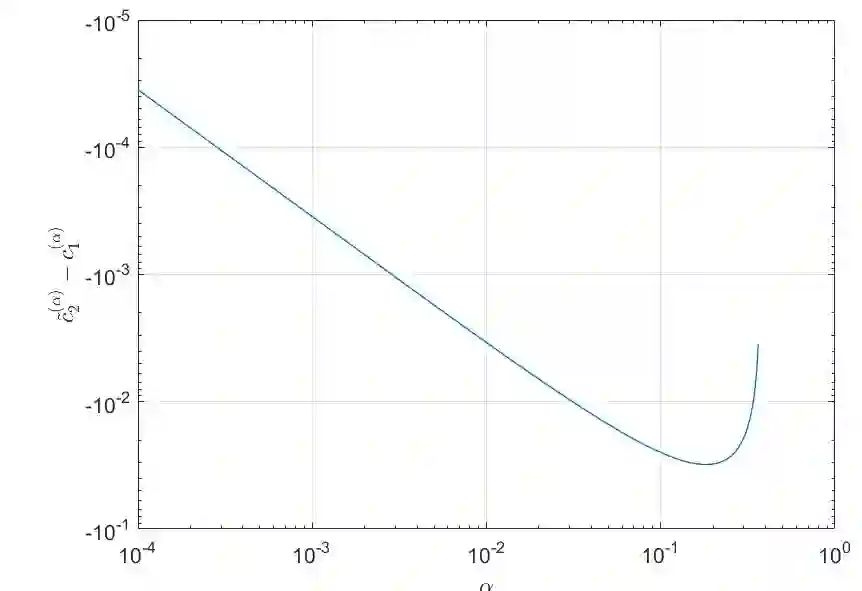
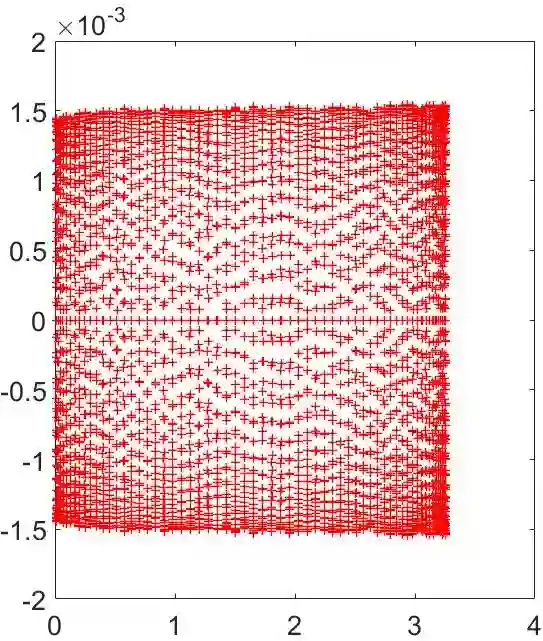
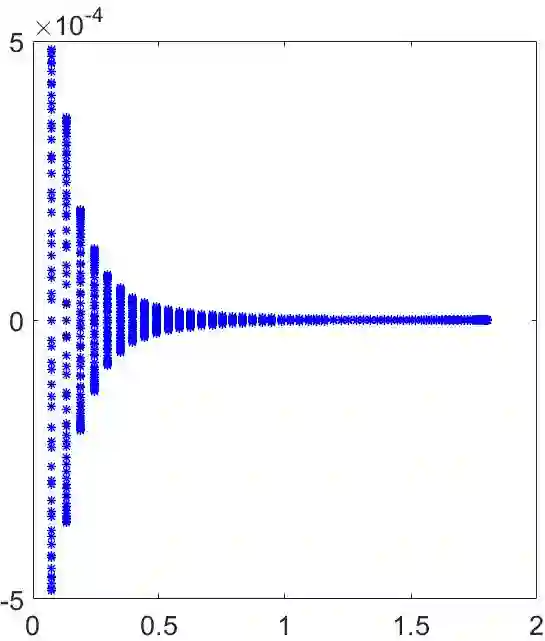
Time-space fractional Bloch-Torrey equations are developed by some researchers to investigate the relationship between diffusion and fractional-order dynamics. In this paper, we first propose a second-order scheme for this equation by employing the recently proposed L2-type formula [A.~A.~Alikhanov, C.~Huang, Appl.~Math.~Comput.~(2021) 126545]. Then, we prove the stability and the convergence of this scheme. Based on such the numerical scheme, a L2-type all-at-once system is derived. In order to solve this system in a parallel-in-time pattern, a bilateral preconditioning technique is designed according to the special structure of the system. We theoretically show that the condition number of the preconditioned matrix is uniformly bounded by a constant for the time fractional order $\alpha \in (0,0.3624)$. Numerical results are reported to show the efficiency of our method.