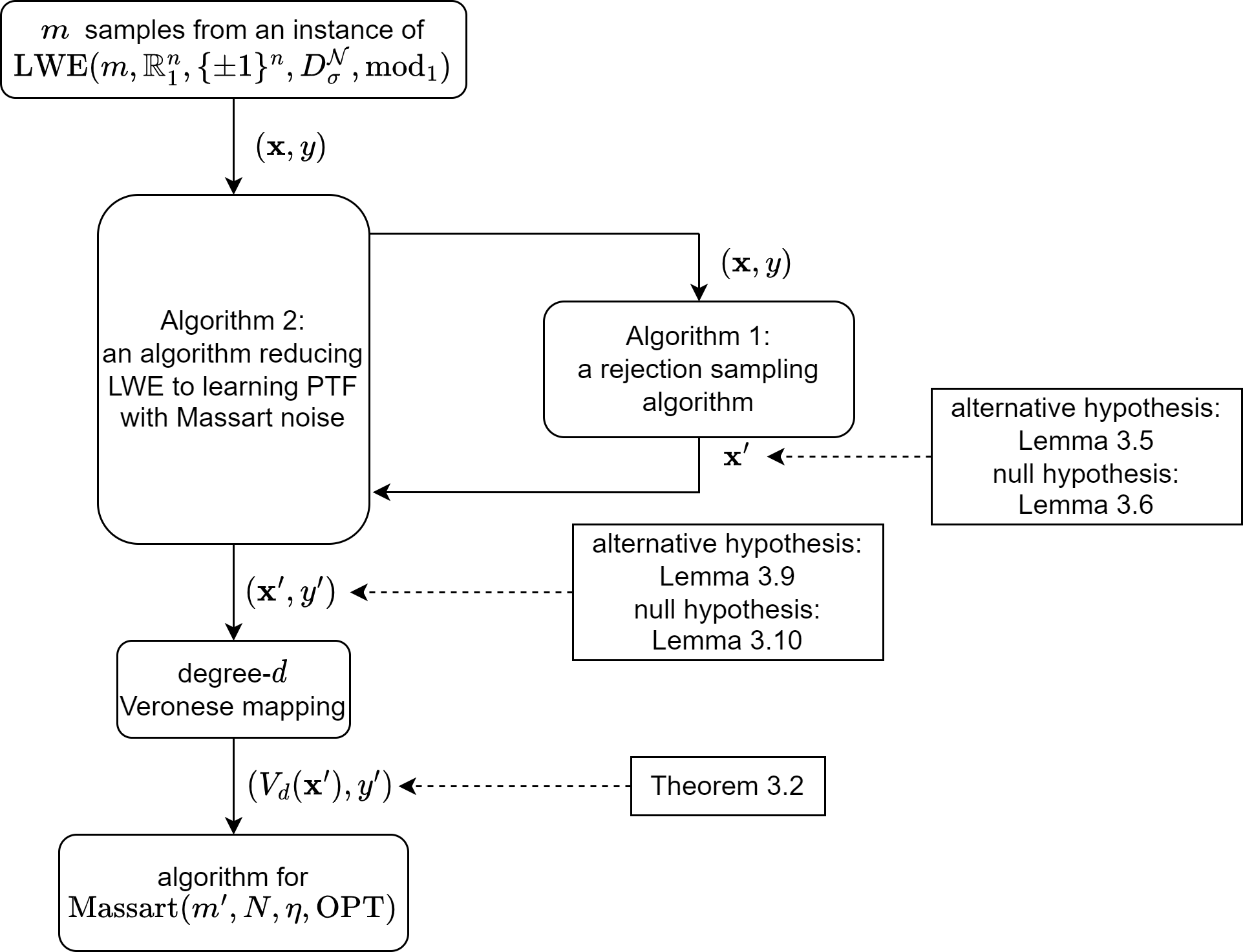
We study the complexity of PAC learning halfspaces in the presence of Massart noise. In this problem, we are given i.i.d. labeled examples $(\mathbf{x}, y) \in \mathbb{R}^N \times \{ \pm 1\}$, where the distribution of $\mathbf{x}$ is arbitrary and the label $y$ is a Massart corruption of $f(\mathbf{x})$, for an unknown halfspace $f: \mathbb{R}^N \to \{ \pm 1\}$, with flipping probability $\eta(\mathbf{x}) \leq \eta < 1/2$. The goal of the learner is to compute a hypothesis with small 0-1 error. Our main result is the first computational hardness result for this learning problem. Specifically, assuming the (widely believed) subexponential-time hardness of the Learning with Errors (LWE) problem, we show that no polynomial-time Massart halfspace learner can achieve error better than $\Omega(\eta)$, even if the optimal 0-1 error is small, namely $\mathrm{OPT} = 2^{-\log^{c} (N)}$ for any universal constant $c \in (0, 1)$. Prior work had provided qualitatively similar evidence of hardness in the Statistical Query model. Our computational hardness result essentially resolves the polynomial PAC learnability of Massart halfspaces, by showing that known efficient learning algorithms for the problem are nearly best possible.
翻译:我们研究 PAC 在 Massart 噪音情况下学习半空的复杂性。 在这个问题中, 我们被给出了 i. d. 标签的示例 $( mathbb{ { murf{x}, y)\ in\ mathbb{R\N\time {\pm 1 \\\\\\ pm 1\\ $美元 美元, 美元是任意的, 标签美元是 Massart 在 Massart 出现 $f( mathb{x} $) 的混杂问题。 对于一个未知的半空 $f:\ mathb{R ⁇ N\ n_N\ to\\\\\\\\\ pma max} 1\ 美元, 标签的示例是 $( massal_ ral_ ral_ ral_ ral_ ral_ral_ral_ral_ral_ral_ral_ral_ral_ral_ ral_ral_ral_ ral_ ral_ ral_ ral_ ral_ ral_ ral_ ral_br_ i_ i_ i), 我们没有多少_l_ lexxxxxl_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_____________l_l__l_l_l_l_l_l_l____l_l_l___l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_l_