Online Kernel CUSUM for Change-Point Detection

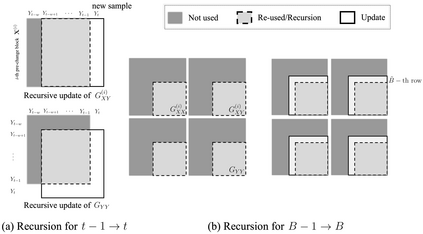
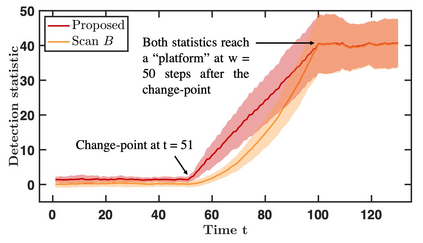
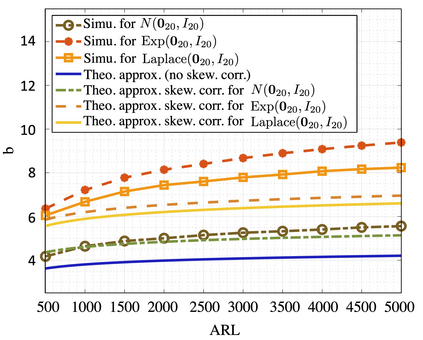
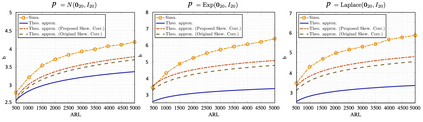
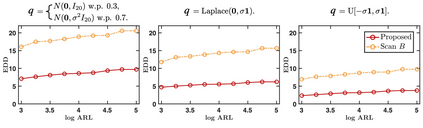
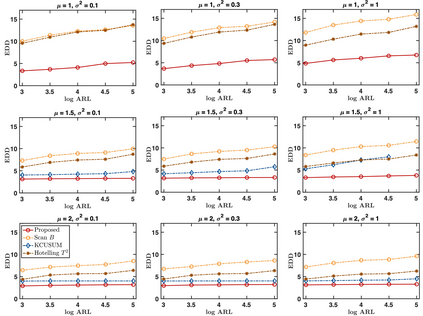
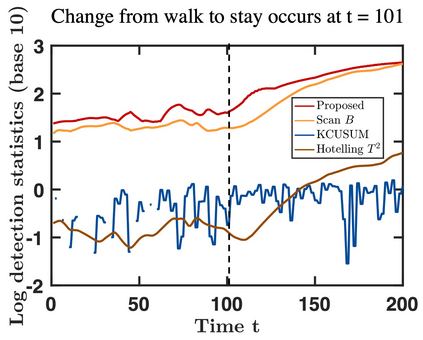
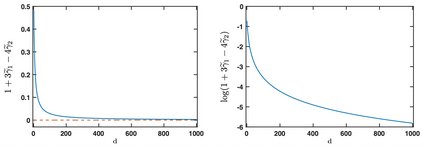
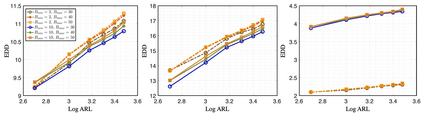
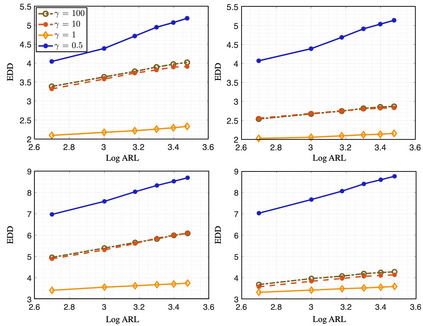
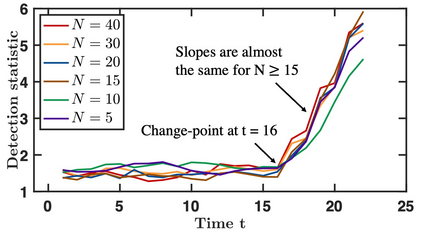
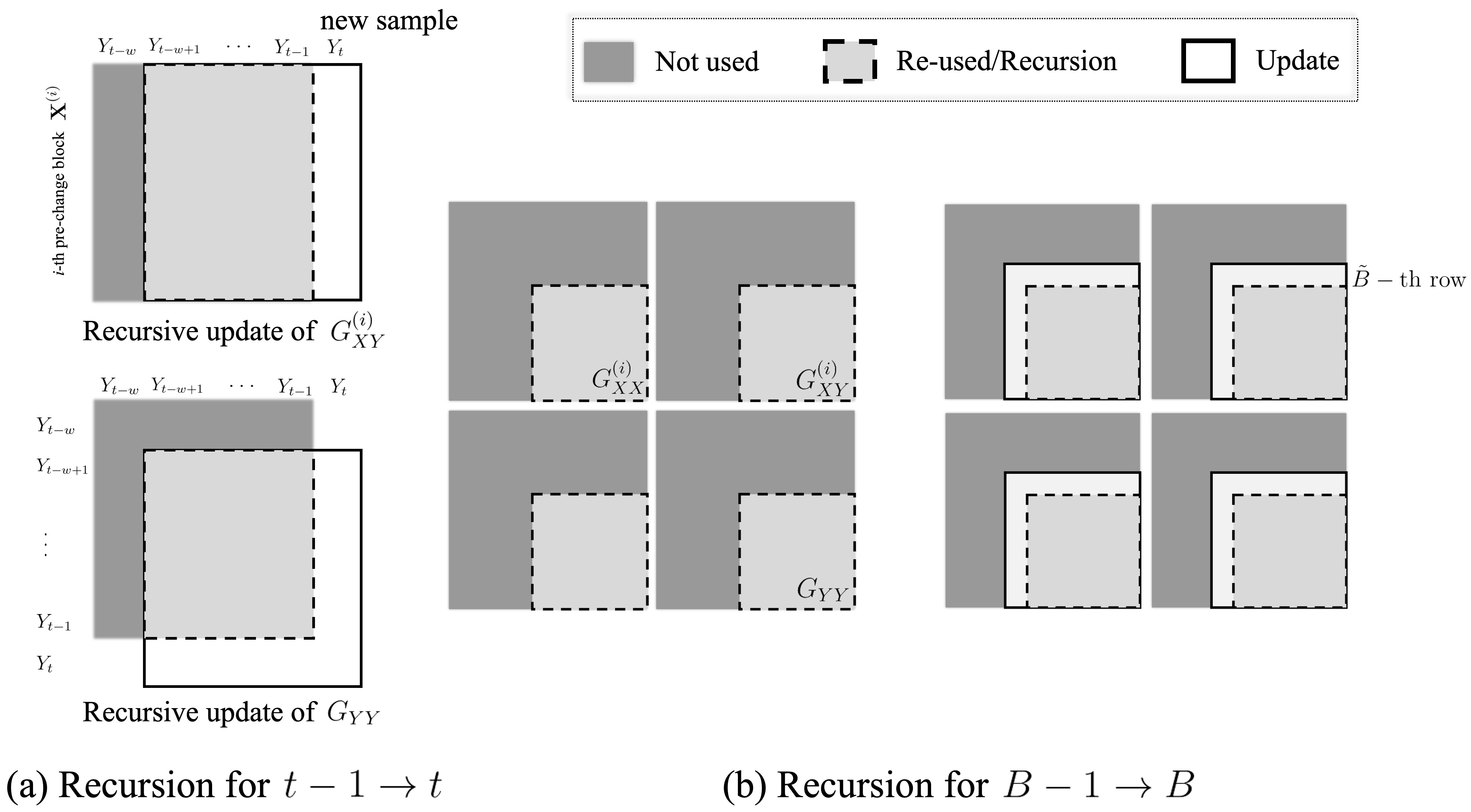
We propose an efficient online kernel Cumulative Sum (CUSUM) method for change-point detection that utilizes the maximum over a set of kernel statistics to account for the unknown change-point location. Our approach exhibits increased sensitivity to small changes compared to existing methods, such as the Scan-B statistic, which corresponds to a non-parametric Shewhart chart-type procedure. We provide accurate analytic approximations for two key performance metrics: the Average Run Length (ARL) and Expected Detection Delay (EDD), which enable us to establish an optimal window length on the order of the logarithm of ARL to ensure minimal power loss relative to an oracle procedure with infinite memory. Such a finding parallels the classic result for window-limited Generalized Likelihood Ratio (GLR) procedure in parametric change-point detection literature. Moreover, we introduce a recursive calculation procedure for detection statistics to ensure constant computational and memory complexity, which is essential for online procedures. Through extensive experiments on both simulated and real data, we demonstrate the competitive performance of our method and validate our theoretical results.