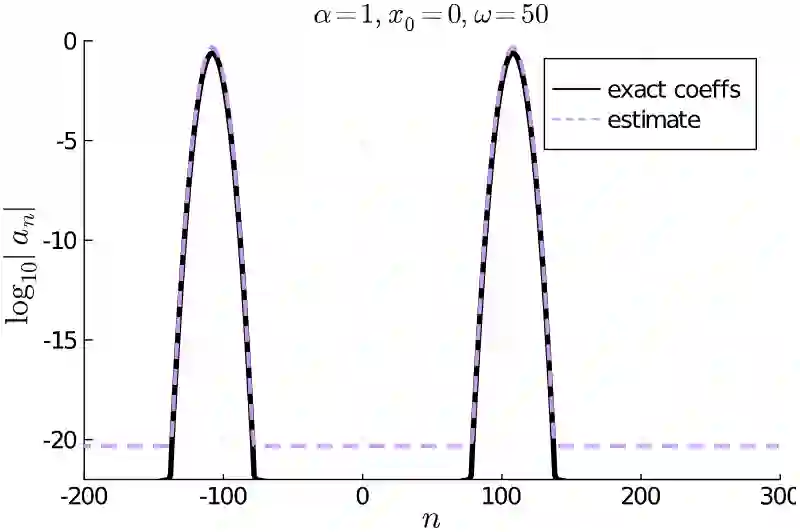
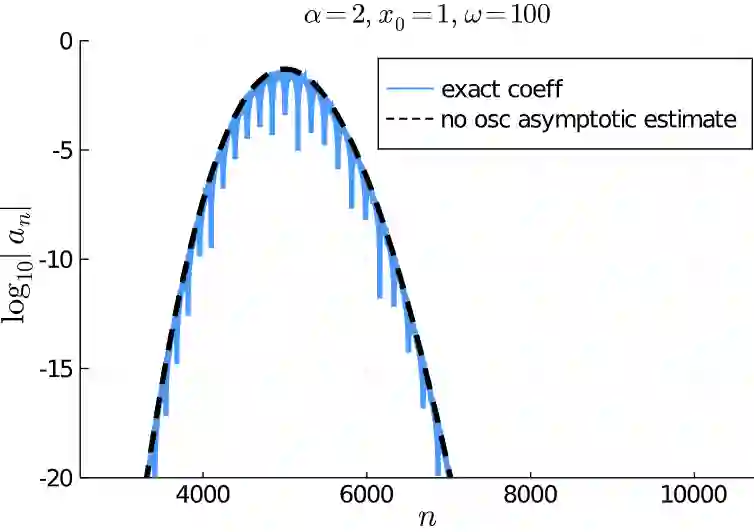
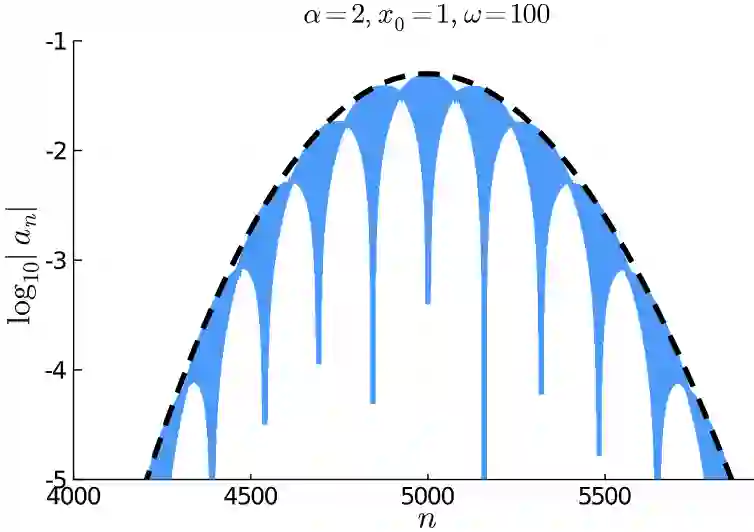
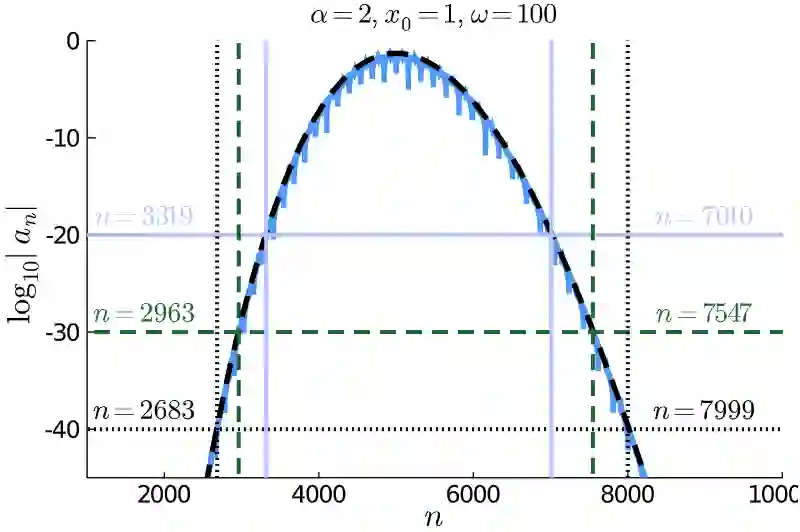
In this paper we compare three different orthogonal systems in $\mathrm{L}_2(\mathbb{R})$ which can be used in the construction of a spectral method for solving the semi-classically scaled time dependent Schr\"odinger equation on the real line, specifically, stretched Fourier functions, Hermite functions and Malmquist--Takenaka functions. All three have banded skew-Hermitian differentiation matrices, which greatly simplifies their implementation in a spectral method, while ensuring that the numerical solution is unitary -- this is essential in order to respect the Born interpretation in quantum mechanics and, as a byproduct, ensures numerical stability with respect to the $\mathrm{L}_2(\mathbb{R})$ norm. We derive asymptotic approximations of the coefficients for a wave packet in each of these bases, which are extremely accurate in the high frequency regime. We show that the Malmquist--Takenaka basis is superior, in a practical sense, to the more commonly used Hermite functions and stretched Fourier expansions for approximating wave packets
翻译:在本文中,我们比较了美元=mathrm{L}2(\\\mathb{R})中的三种不同的正方形系统,这些系统可用于在实线上构建一个光谱方法,以解决半经典缩放时间依赖 Schr\'donger 方程式,具体地说,是拉伸的 Fourier 函数、 Hermite 函数和 Malmquist- Pakenaka 函数。这三个系统都有带宽的斜带- Hermitian 差异矩阵,它们大大简化了在光谱方法中的实施,同时确保数字解决方案是统一的 -- -- 这对于量子力学的诞生解释至关重要,并且作为一个副产品,确保了美元\ mathrm{L\\\\\\\\\\\\\\\\\\\\\\ mathb{R} 标准的数字稳定性。我们从这些基底座中每个波包的系数中得出无症状的近似值,这在高频率系统中是非常精确的。我们显示, 马尔基- 竹纳卡基基础实际上优于更常用的赫姆特函数和波状容器。