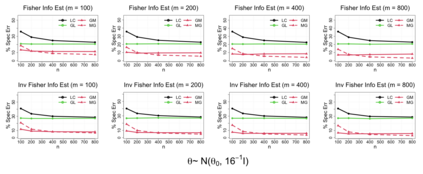
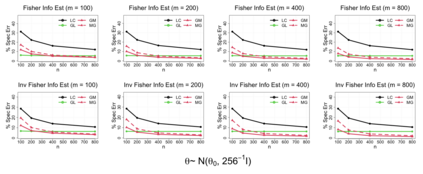
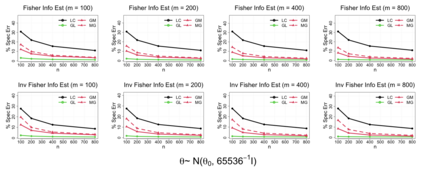
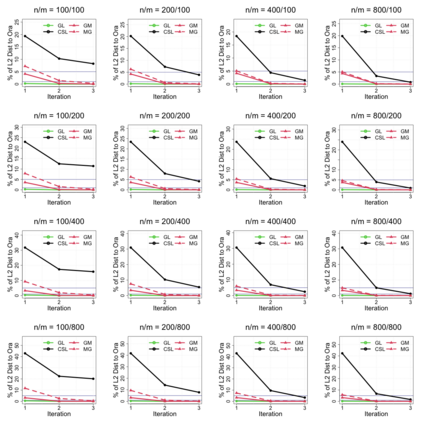
In modern data science, it is common that large-scale data are stored and processed parallelly across a great number of locations. For reasons including confidentiality concerns, only limited data information from each parallel center is eligible to be transferred. To solve these problems more efficiently, a group of communication-efficient methods are being actively developed. We propose two communication-efficient Newton-type algorithms, combining the M-estimator and the gradient collected from each data center. They are created by constructing two Fisher information estimators globally with those communication-efficient statistics. Enjoying a higher rate of convergence, this framework improves upon existing Newton-like methods. Moreover, we present two bias-adjusted one-step distributed estimators. When the square of the center-wise sample size is of a greater magnitude than the total number of centers, they are as efficient as the global $M$-estimator asymptotically. The advantages of our methods are illustrated by extensive theoretical and empirical evidences.
翻译:在现代数据科学中,大量数据在众多地点同时储存和处理,这是很常见的。由于保密问题等原因,每个平行中心只有有限的数据信息才有资格被转让。为了更有效率地解决这些问题,正在积极开发一套通信效率高的方法。我们建议采用两种通信效率高的牛顿型算法,将M-估计和从每个数据中心收集的梯度结合起来。它们是通过在全球建设两个渔业信息估计员和这些通信效率高的统计数据来创建的。由于实现了更高的趋同率,这个框架改进了现有的牛顿式方法。此外,我们提出了两个偏差调整的一步分布式估计数字。当中点样本面积的方形比中心总数大时,它们的效率与全球$M$-估计器一样。我们方法的优点通过广泛的理论和经验证据来说明。