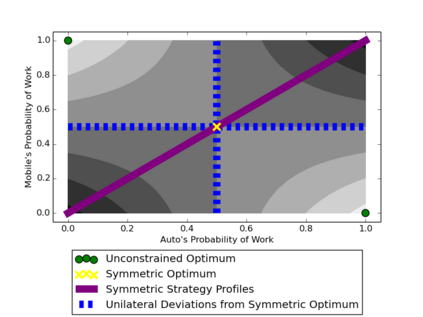
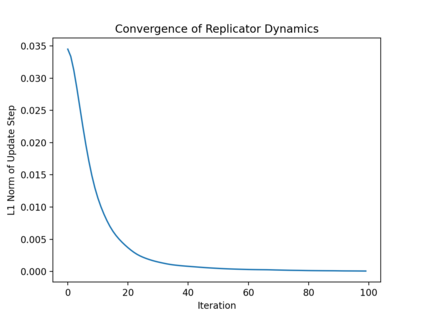
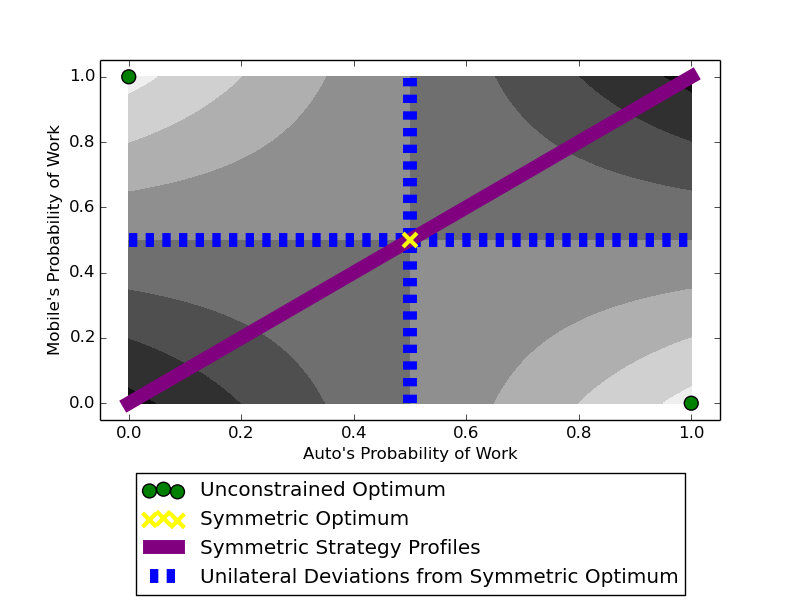
Although it has been known since the 1970s that a globally optimal strategy profile in a common-payoff game is a Nash equilibrium, global optimality is a strict requirement that limits the result's applicability. In this work, we show that any locally optimal symmetric strategy profile is also a (global) Nash equilibrium. Furthermore, we show that this result is robust to perturbations to the common payoff and to the local optimum. Applied to machine learning, our result provides a global guarantee for any gradient method that finds a local optimum in symmetric strategy space. While this result indicates stability to unilateral deviation, we nevertheless identify broad classes of games where mixed local optima are unstable under joint, asymmetric deviations. We analyze the prevalence of instability by running learning algorithms in a suite of symmetric games, and we conclude by discussing the applicability of our results to multi-agent RL, cooperative inverse RL, and decentralized POMDPs.
翻译:尽管自1970年代以来人们就知道,在共同减税游戏中,全球最佳战略概况是纳什平衡,但全球最佳是限制结果适用性的严格要求。在这项工作中,我们表明,任何地方最佳对称战略概况也是(全球)纳什平衡。此外,我们表明,这一结果对于影响共同得益和当地最佳得益十分有利。应用于机器学习,我们的结果为任何在对称战略空间中找到地方最佳取向的梯度方法提供了全球保障。虽然这一结果表明单方面偏差具有稳定性,但我们还是确定了当地混合选制在联合、不对称偏差下不稳定的各类游戏。我们通过在一系列对称游戏中运行学习算法来分析不稳定的普遍程度,我们最后通过讨论我们的结果对多试剂RL、反合作RL和分散的POMDP的适用性。