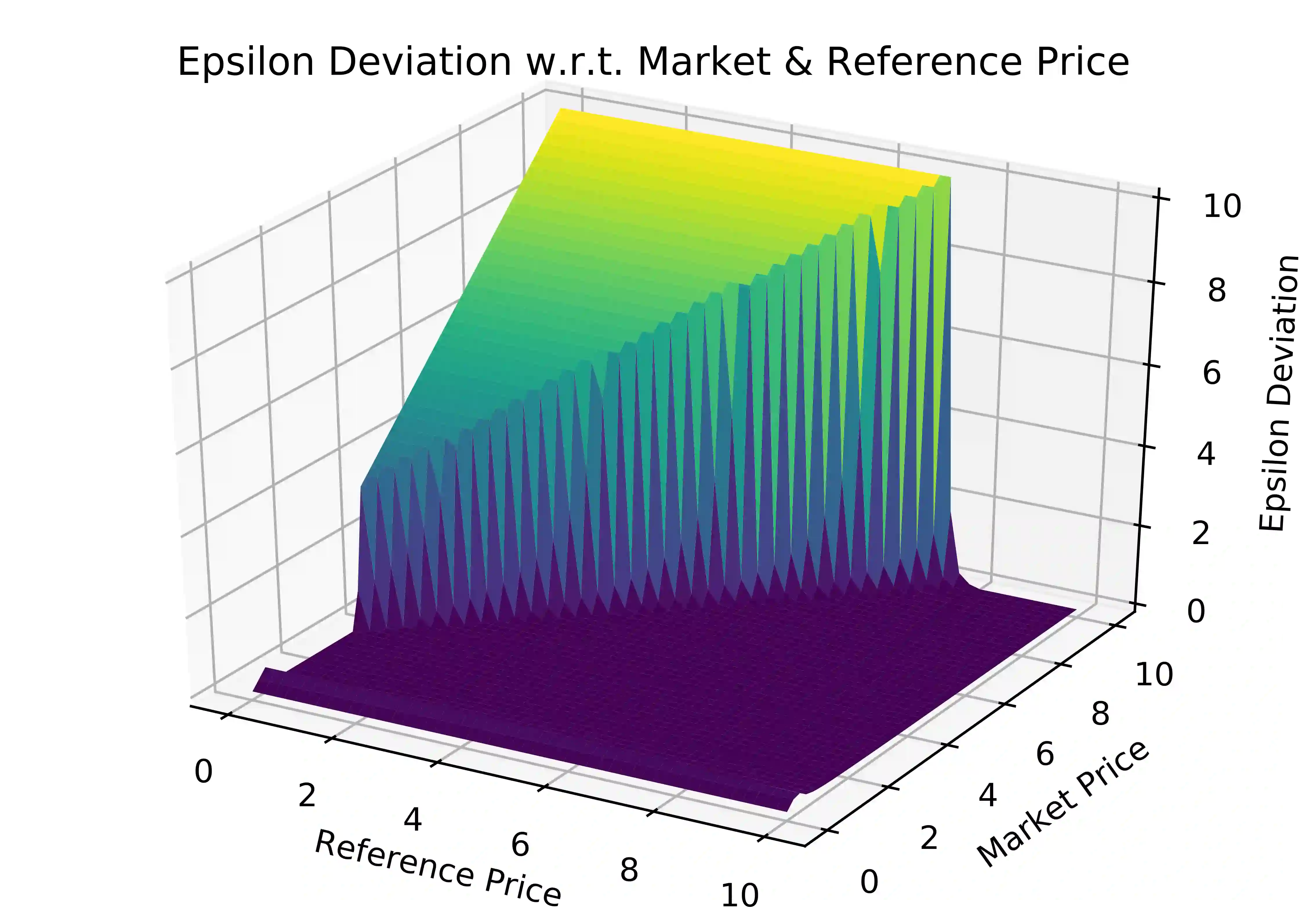
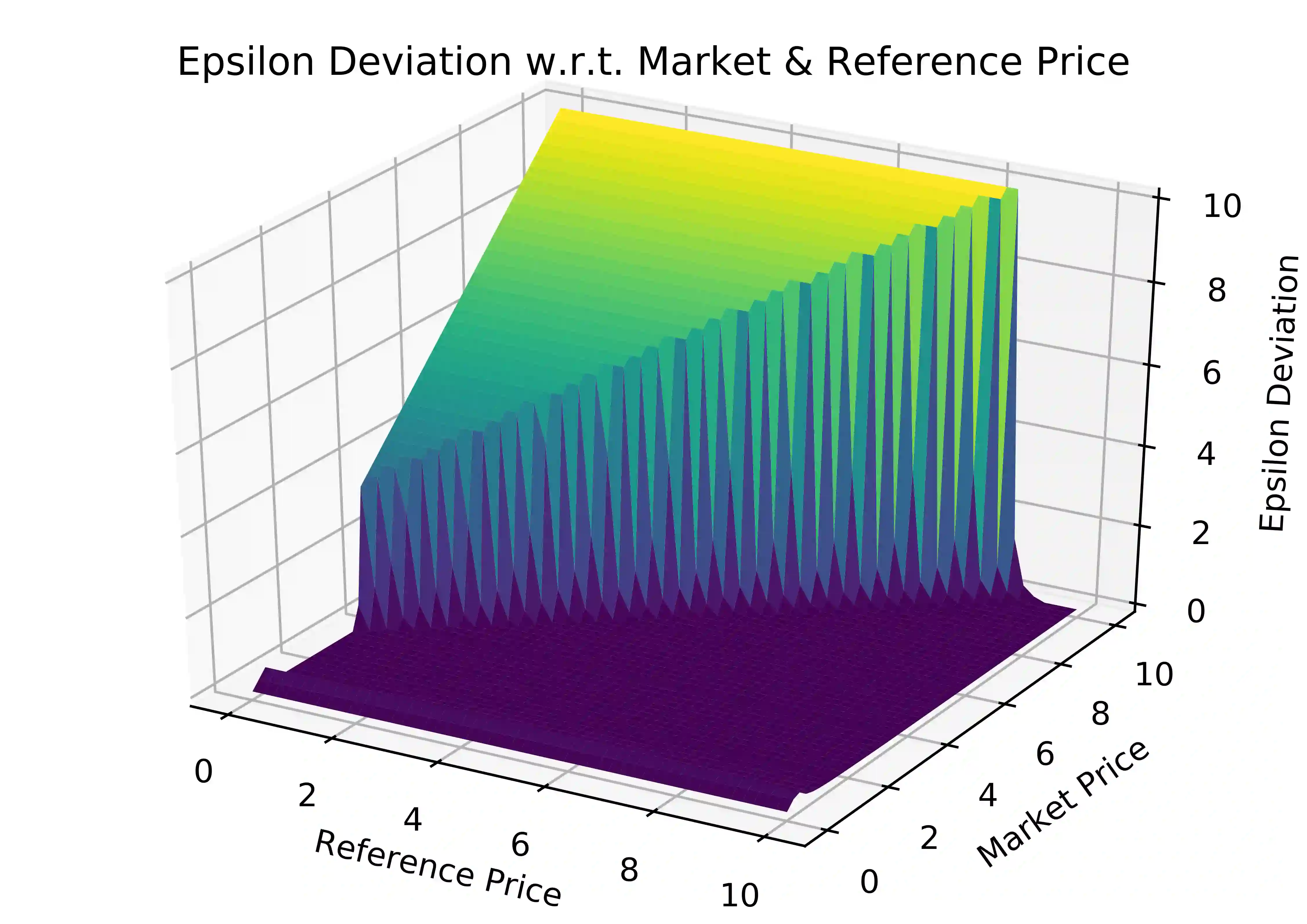
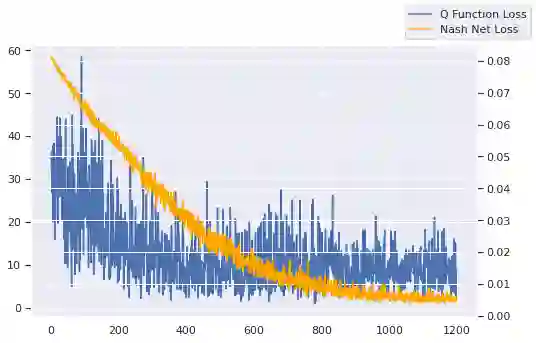
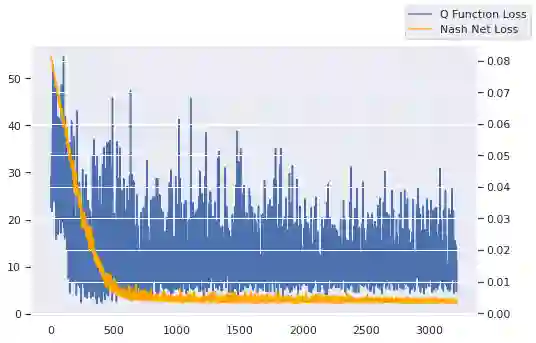
We investigate Nash equilibrium learning in a competitive Markov Game (MG) environment, where multiple agents compete, and multiple Nash equilibria can exist. In particular, for an oligopolistic dynamic pricing environment, exact Nash equilibria are difficult to obtain due to the curse-of-dimensionality. We develop a new model-free method to find approximate Nash equilibria. Gradient-free black box optimization is then applied to estimate $\epsilon$, the maximum reward advantage of an agent unilaterally deviating from any joint policy, and to also estimate the $\epsilon$-minimizing policy for any given state. The policy-$\epsilon$ correspondence and the state to $\epsilon$-minimizing policy are represented by neural networks, the latter being the Nash Policy Net. During batch update, we perform Nash Q learning on the system, by adjusting the action probabilities using the Nash Policy Net. We demonstrate that an approximate Nash equilibrium can be learned, particularly in the dynamic pricing domain where exact solutions are often intractable.
翻译:我们在竞争激烈的Markov游戏(MG)环境中调查纳什平衡学习,在这个环境中,多个代理商可以相互竞争,多个纳什平衡可以存在。特别是,对于寡头主义动态定价环境,由于维度的诅咒,很难获得准确的纳什平衡。我们开发了一种新的无模式方法来寻找大约纳什平衡。然后,将无梯度黑盒优化用于估算美元,即单方面偏离任何联合政策的代理商的最大奖赏优势,并且还估算任何特定州以美元为最小化的政策。政策-美元-百分率通信和以美元为最小化的政策由神经网络代表,后者是纳什政策网。在批次更新过程中,我们通过调整使用纳什政策网的行动概率,在系统上学习纳什Q。我们证明,可以学习到一种近似纳什平衡,特别是在动态定价领域,确切的解决方案往往难以解决。