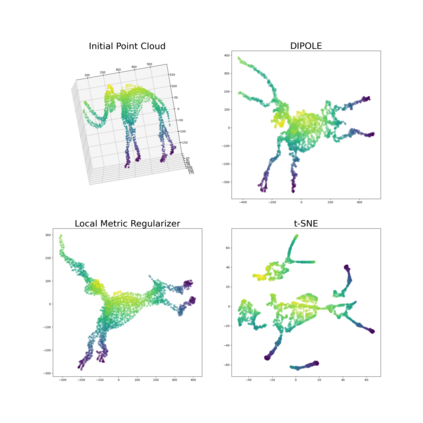
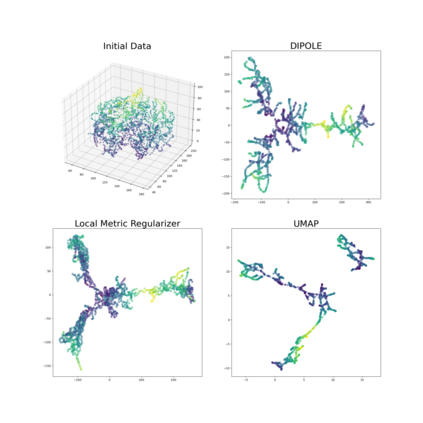
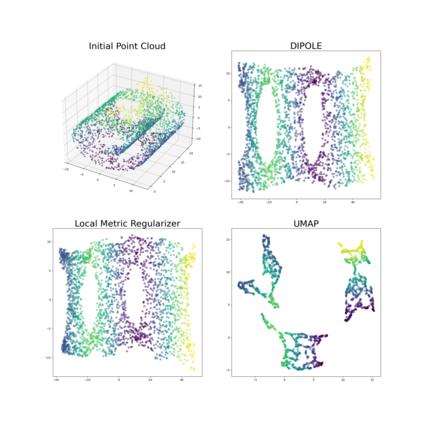
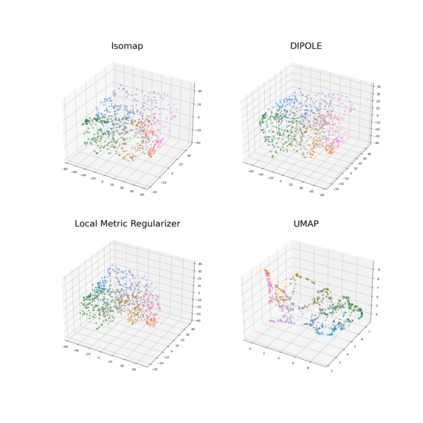
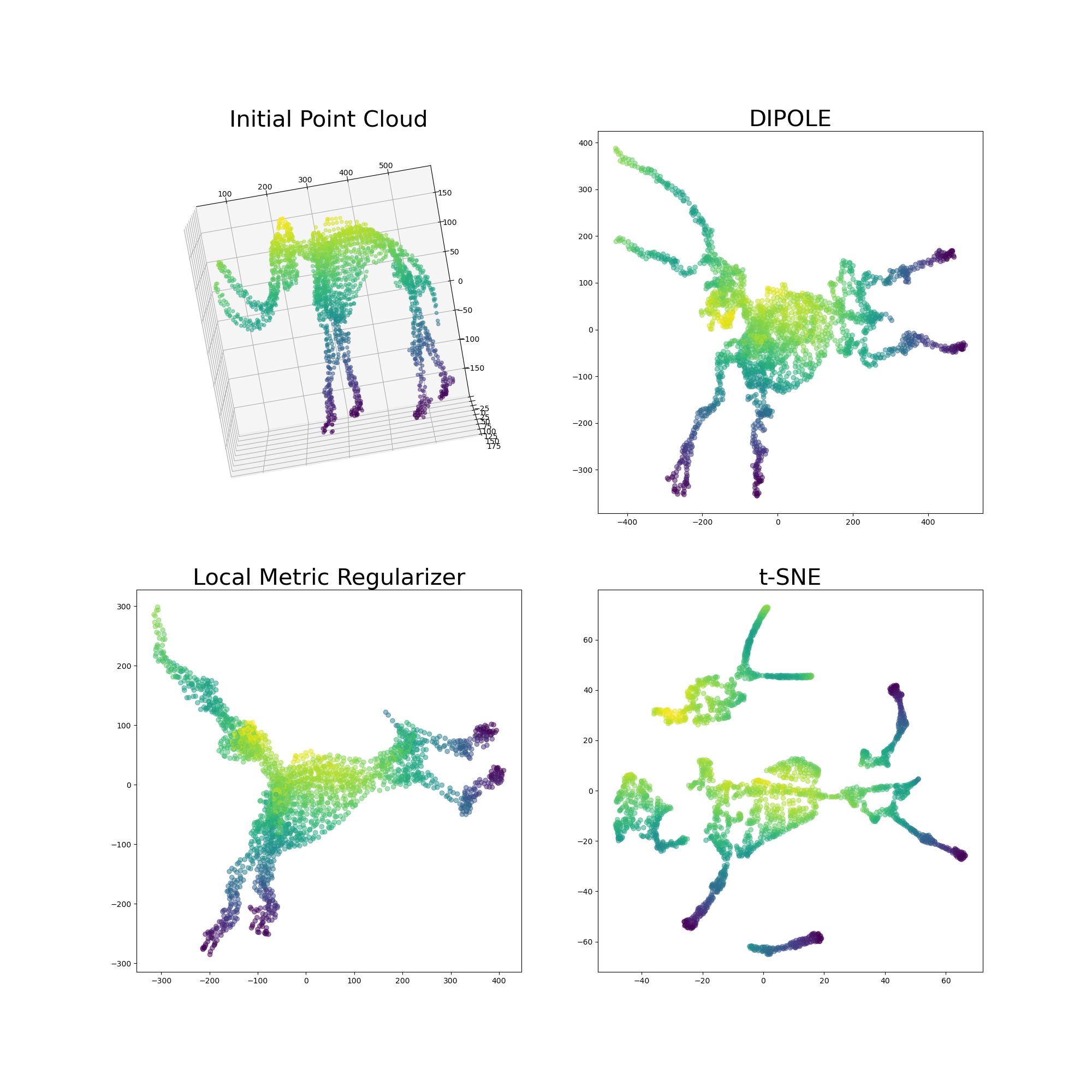
We propose a novel approach to dimensionality reduction combining techniques of metric geometry and distributed persistent homology, in the form of a gradient-descent based method called DIPOLE. DIPOLE is a dimensionality-reduction post-processing step that corrects an initial embedding by minimizing a loss functional with both a local, metric term and a global, topological term. By fixing an initial embedding method (we use Isomap), DIPOLE can also be viewed as a full dimensionality-reduction pipeline. This framework is based on the strong theoretical and computational properties of distributed persistent homology and comes with the guarantee of almost sure convergence. We observe that DIPOLE outperforms popular methods like UMAP, t-SNE, and Isomap on a number of popular datasets, both visually and in terms of precise quantitative metrics.
翻译:我们建议采用新的方法,结合量度几何和分布式持久性同质学技术,采用以梯度-白种为基础的方法DIPOLE。DIPOLE是一种以梯度-白种为基础的方法。DIPOLE是一种减少梯度-后处理步骤,它纠正了最初的嵌入过程,将损失功能与当地、计量术语和全球的地形术语相最小化。通过确定初始嵌入方法(我们使用Isomap),DIPOLE也可以被视为一种完全的维度-减少管道。这个框架基于分布式的持久性同质学的强烈理论和计算特性,并具有几乎可以肯定的趋同的保证。我们观察到DIPOLE在视觉和精确的定量指标方面,都比UMAP、t-SNE和Isomap等一些流行的数据集的流行方法要优于UMAP、t-SNE和Isomap。