Space-time POD-Galerkin approach for parametric flow control

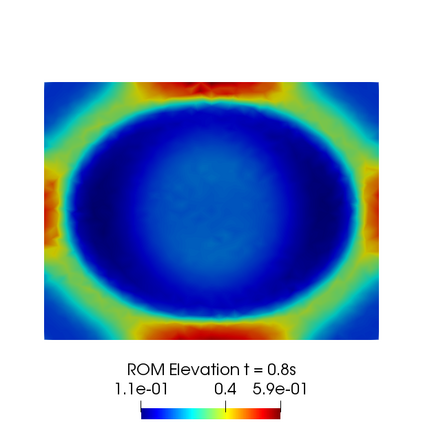
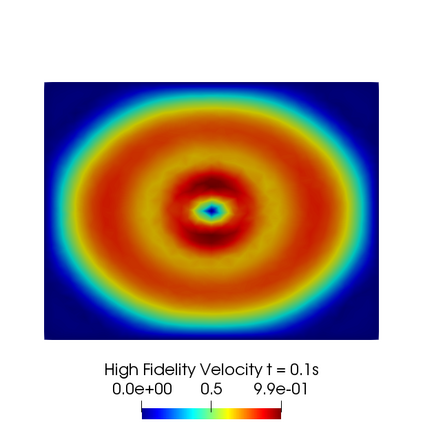
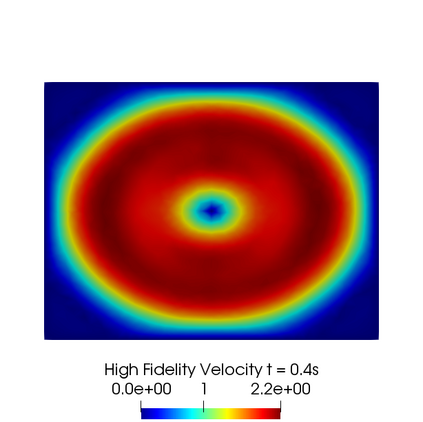
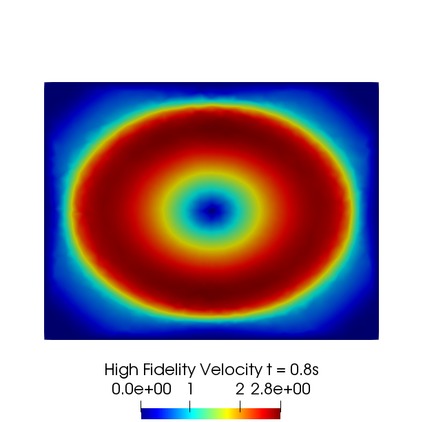
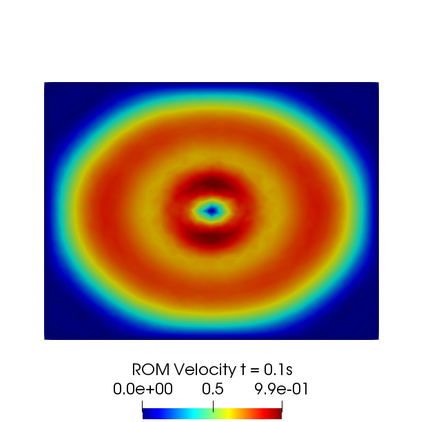
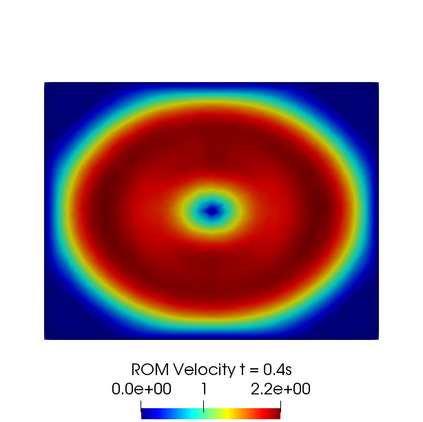
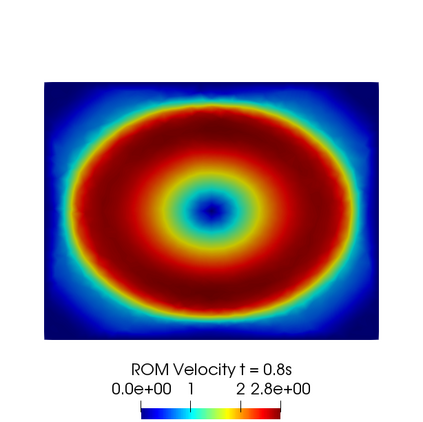
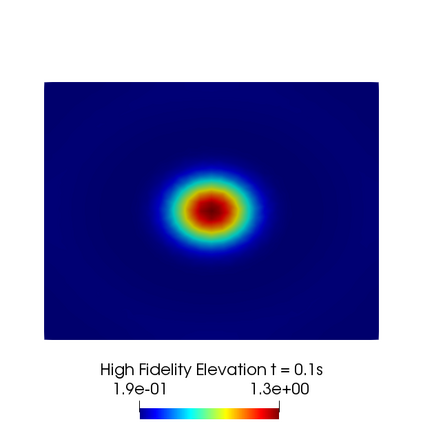
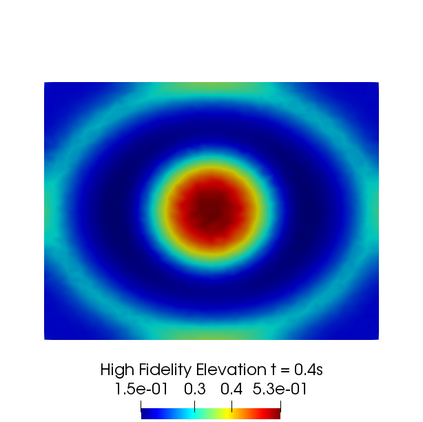
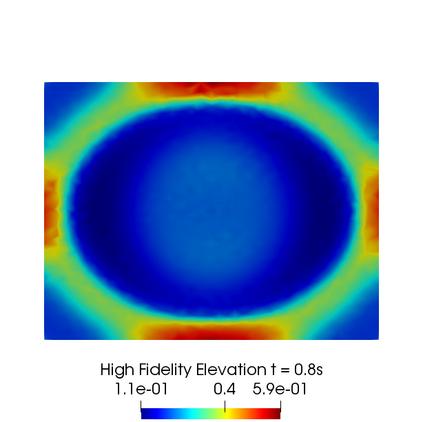
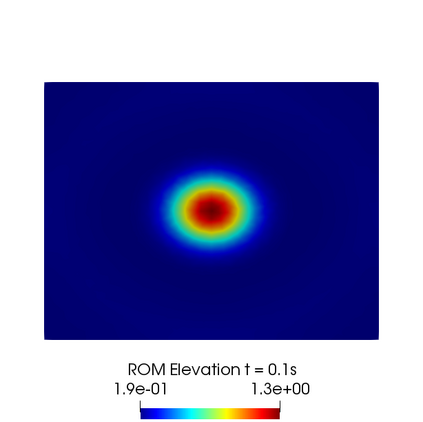
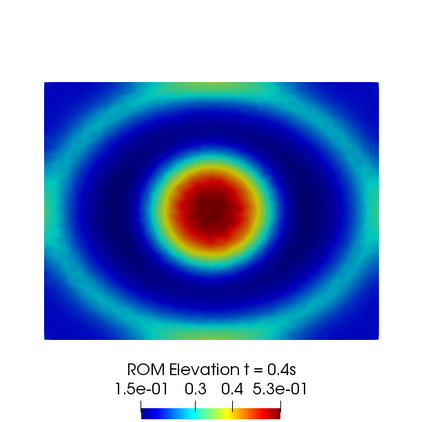
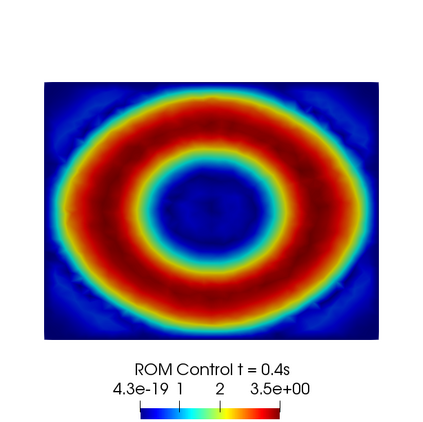
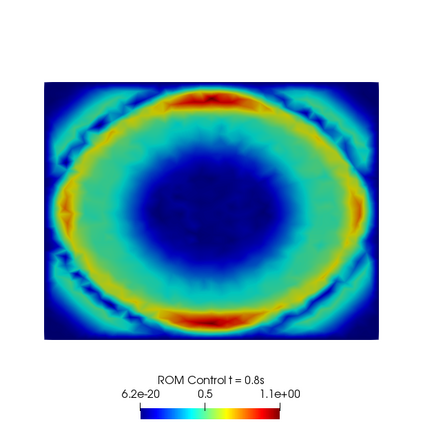
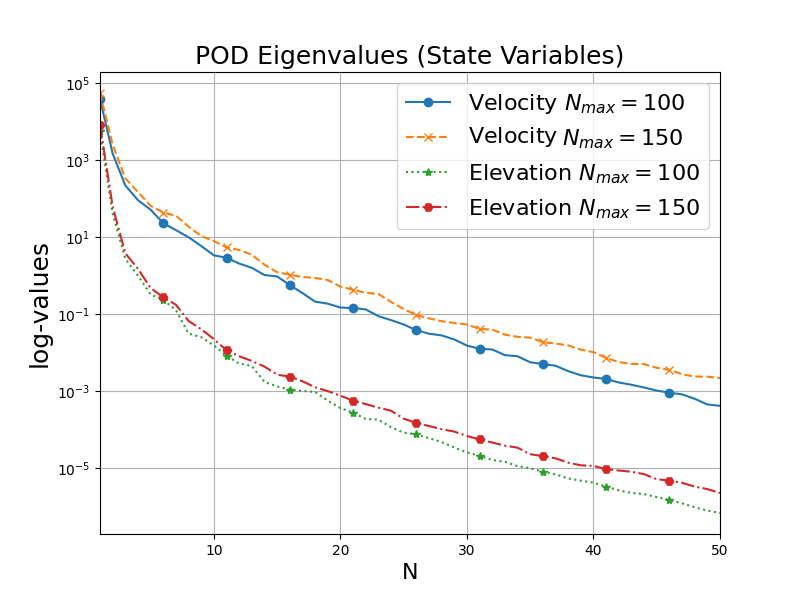
In this contribution we propose reduced order methods to fast and reliably solve parametrized optimal control problems governed by time dependent nonlinear partial differential equations. Our goal is to provide a tool to deal with the time evolution of several nonlinear optimality systems in many-query context, where a system must be analysed for various physical and geometrical features. Optimal control can be used in order to fill the gap between collected data and mathematical model and it is usually related to very time consuming activities: inverse problems, statistics, etc. Standard discretization techniques may lead to unbearable simulations for real applications. We aim at showing how reduced order modelling can solve this issue. We rely on a space-time POD-Galerkin reduction in order to solve the optimal control problem in a low dimensional reduced space in a fast way for several parametric instances. The proposed algorithm is validated with a numerical test based on environmental sciences: a reduced optimal control problem governed by viscous Shallow Waters Equations parametrized not only in the physics features, but also in the geometrical ones. We will show how the reduced model can be useful in order to recover desired velocity and height profiles more rapidly with respect to the standard simulation, not losing accuracy.