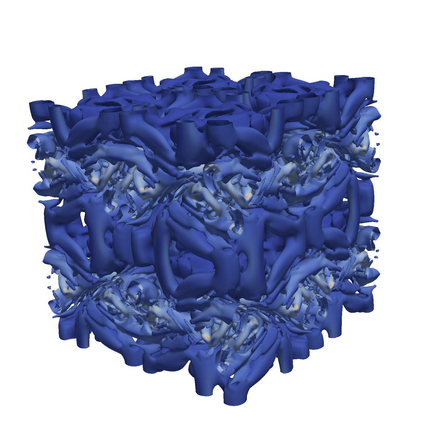
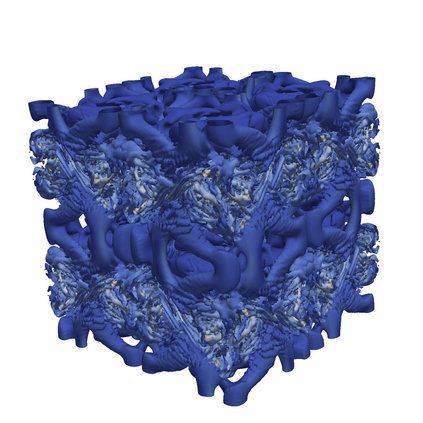
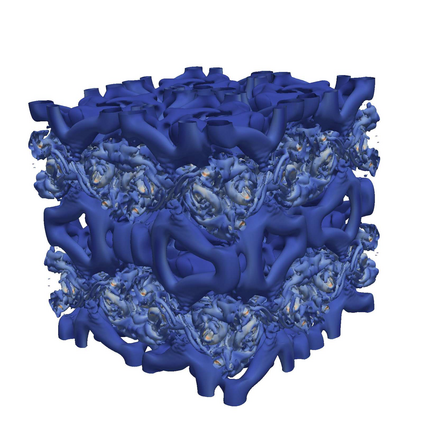
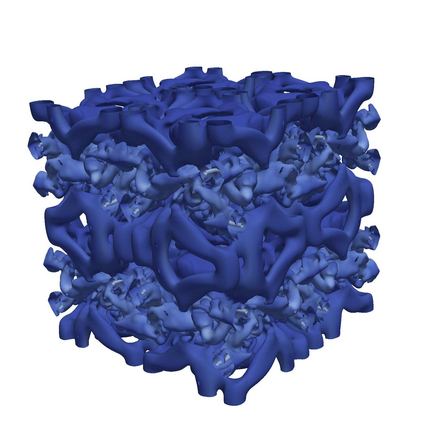
Residual and solution filtering procedures are studied with respect to inhibiting the accumulation of small-scale (i.e., high wavenumber) content. Assessing each method in terms of an ``equivalent residual equation" reveals fundamental differences in their behaviors, such as how the underlying solution can be constrained to a target filter width. The residual filtering (RF) approach paired with a dissipative filter kernel is shown to restrict scale generation in the fluid equations via dispersive effects; meanwhile, solution filtering (SF) -- and artificial dissipation (AD), by extension -- operates through dissipative mechanisms and actively attenuates high wavenumber content. Discrete filters (i.e., the Top-hat and implicit Tangent schemes) are analyzed in terms of their response characteristics and their associated effects on reducing small-scale activity when paired with the RF versus SF approaches. Linear theoretical assessments (e.g., von Neumann analysis) are shown to successfully characterize the fundamental behaviors of the methods in non-linear settings, as observed through canonical test cases based on 1D viscous Burgers, 2D Euler, 3D Navier-Stokes equations.
翻译:----
研究了残差过滤和溶液过滤程序在抑制小尺度(即高波数)内容积累方面的特点。通过评估每种方法的“等效残差方程”,揭示了它们之间的根本差异,例如,如何将基础解约束为目标滤波器宽度。残差过滤(RF)方法配合耗散滤波核被证明通过色散效应限制流体方程中的尺度生成;同时,溶液过滤(SF)-并由此推广的人工耗散-则通过耗散机制运作并从根本上减缓高波数内容。在RF和SF方法配对的情况下,分析了离散滤波器(即Top-hat和implicit Tangent方案)的响应特性和它们在减少小尺度活动时产生的影响。线性理论评估(例如von Neumann分析)被证明可以成功地表征非线性设置中方法的基本行为,如基于1D粘性Burgers、2D欧拉、3D Navier-Stokes方程的经典测试案例所观察到的。