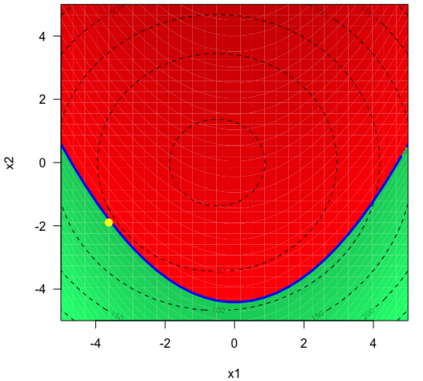
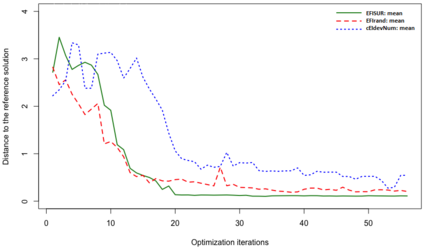
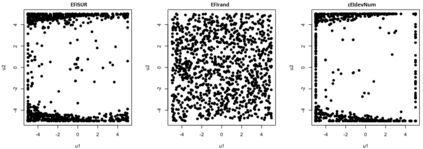
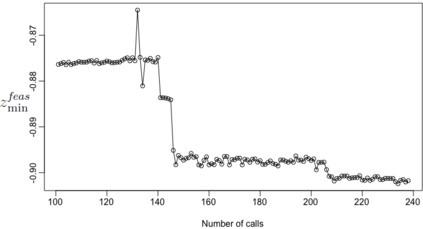
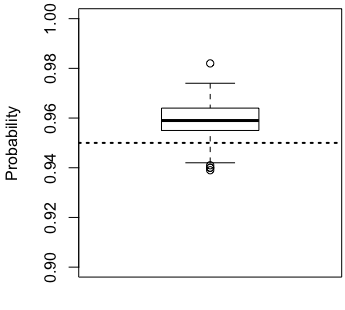
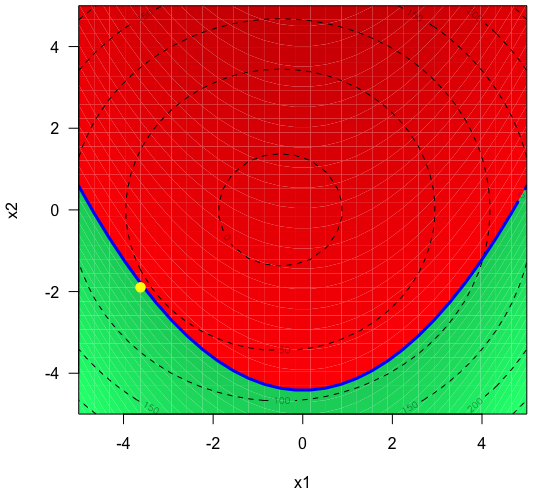
We consider the problem of chance constrained optimization where it is sought to optimize a function and satisfy constraints, both of which are affected by uncertainties. The real world declinations of this problem are particularly challenging because of their inherent computational cost. To tackle such problems, we propose a new Bayesian optimization method. It applies to the situation where the uncertainty comes from some of the inputs, so that it becomes possible to define an acquisition criterion in the joint controlled-uncontrolled input space. The main contribution of this work is an acquisition criterion that accounts for both the average improvement in objective function and the constraint reliability. The criterion is derived following the Stepwise Uncertainty Reduction logic and its maximization provides both optimal controlled and uncontrolled parameters. Analytical expressions are given to efficiently calculate the criterion. Numerical studies on test functions are presented. It is found through experimental comparisons with alternative sampling criteria that the adequation between the sampling criterion and the problem contributes to the efficiency of the overall optimization. As a side result, an expression for the variance of the improvement is given.
翻译:我们考虑了机会限制优化问题,因为希望优化功能和满足制约,两者都受到不确定因素的影响。这个问题的实际世界分解由于其内在计算成本而特别具有挑战性。为了解决这些问题,我们提出了新的巴伊西亚优化方法。我们提出新的巴伊西亚优化方法。它适用于不确定性来自某些投入的情况,从而有可能在联合控制下不受控制的投入空间中确定获取标准。这项工作的主要贡献是获取标准,既考虑到客观功能的平均改进,又考虑到制约可靠性。该标准是在 " 步进不确定减少逻辑 " 之后得出的,其最大化提供了最佳的控制性和不受控制的参数。分析表达方式是为了有效地计算标准。关于测试功能的量化研究被提出,通过实验性比较与替代抽样标准发现,取样标准和问题之间的偏差有助于总体优化的效率。另一方面,还给出了改进差异的表达方式。