Bayesian Graph Neural Network for Fast identification of critical nodes in Uncertain Complex Networks

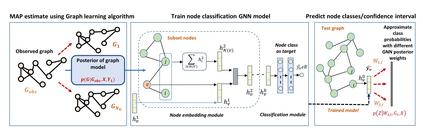
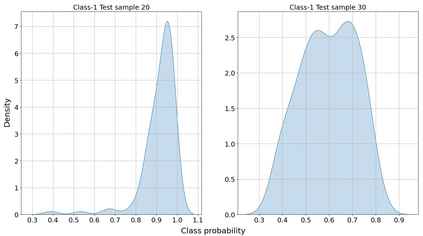
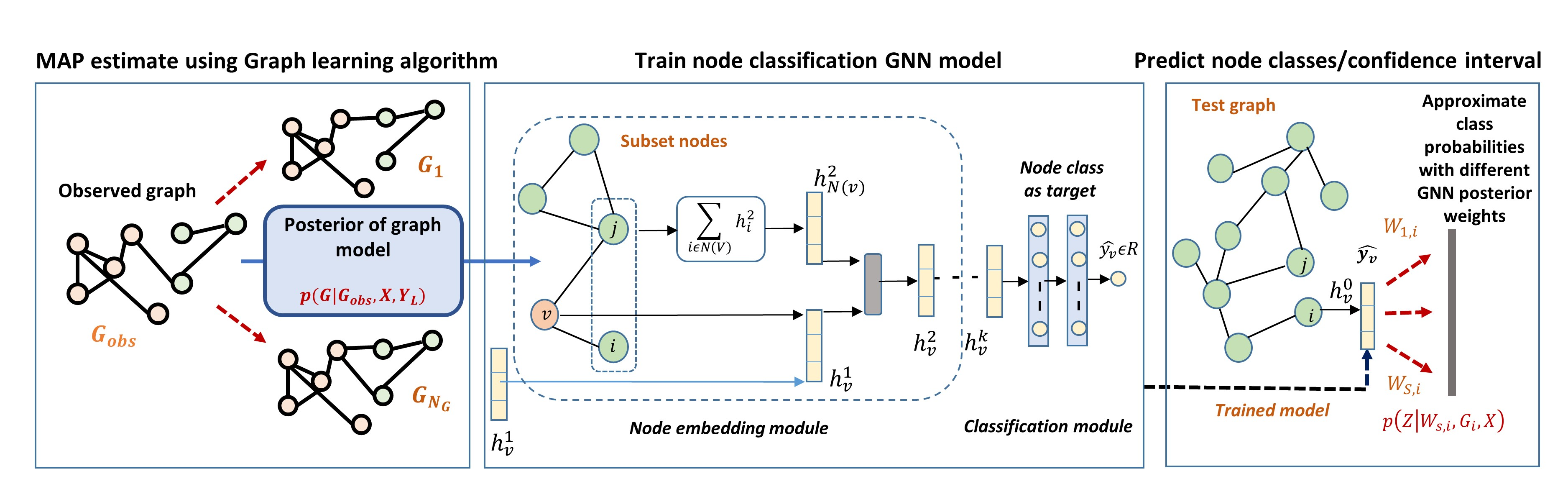
In the quest to improve efficiency, interdependence and complexity are becoming defining characteristics of modern complex networks representing engineered and natural systems. Graph theory is a widely used framework for modeling such complex networks and to evaluate their robustness to disruptions. Particularly, identification of critical nodes/links in a graph can facilitate the enhancement of graph (system) robustness and characterize crucial factors of system performance. Most existing methods of critical node identification are based on an iterative approach that explores each node/link of a graph. These methods suffer from high computational complexity and the resulting analysis is network specific. Additionally, uncertainty associated with the underlying graphical model further limits the potential value of these traditional approaches. To overcome these challenges, we propose a Bayesian graph neural network based node classification framework that is computationally efficient and systematically incorporates uncertainties. Instead of utilizing the observed graph for training the model, a MAP estimate of the graph is computed based on the observed topology and node target labels. Further, a Monte-Carlo (MC) dropout algorithm is incorporated to account for the epistemic uncertainty. The fidelity and the gain in computational complexity offered by the Bayesian framework is illustrated using simulation results.