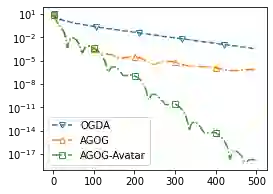
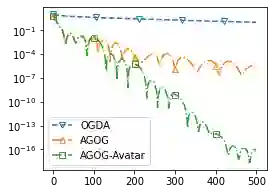
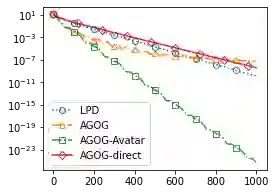
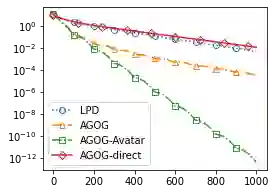
We provide a novel first-order optimization algorithm for bilinearly-coupled strongly-convex-concave minimax optimization called the AcceleratedGradient OptimisticGradient (AG-OG). The main idea of our algorithm is to leverage the structure of the considered minimax problem and operates Nesterov's acceleration on the individual part and optimistic gradient on the coupling part of the objective. We motivate our method by showing that its continuous-time dynamics corresponds to an organic combination of the dynamics of optimistic gradient and of Nesterov's acceleration. By discretizing the dynamics we conclude polynomial convergence behavior in discrete time. Further enhancement of AG-OG with proper restarting allows us to achieve rate-optimal (up to a constant) convergence rates with respect to the conditioning of the coupling and individual parts, which results in the first single-call algorithm achieving improved convergence in the deterministic setting and rate-optimality in the stochastic setting under bilinearly coupled minimax problem sets.
翻译:我们为双线混合的强精密凝固小型最大最大优化提供了一种新型的第一阶优化算法,称为加速进取最佳乐观度(AG-OG),我们的主要算法思想是利用所考虑的微型问题的结构,对内斯特罗夫的个别加速和对目标的结合部分的乐观梯度进行操作。我们通过显示其连续时间动态与乐观梯度动态和内斯特罗夫加速度动态的有机组合相对应。我们通过分解动态,在离散时间完成多元趋同行为。进一步加强AG-OG,适当重新启动,使我们能够在组合和个别部分的调节方面实现速率最佳(达到恒定值)趋同率,从而导致第一次单调算算法在确定性设置和速率最优性方面实现更好的趋同,在双线结合的小型问题组合下,在随机环境下,使速率最优化的趋同。