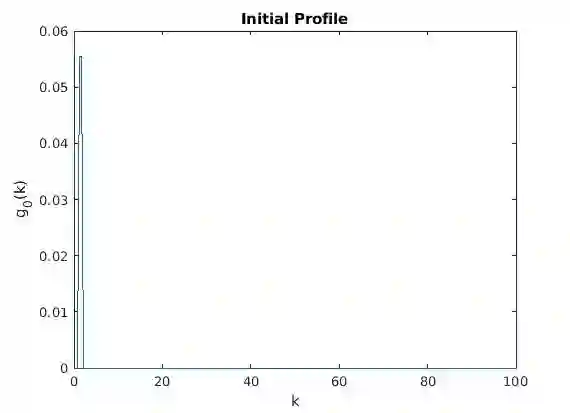
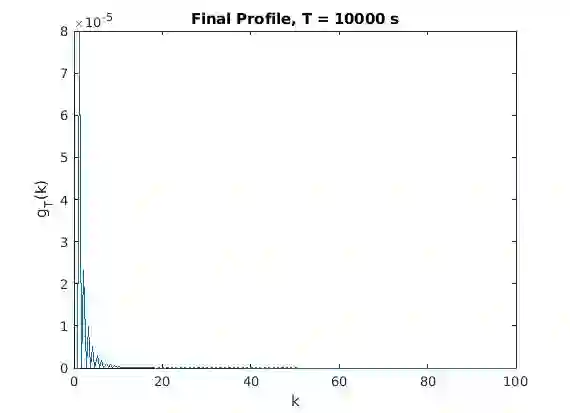
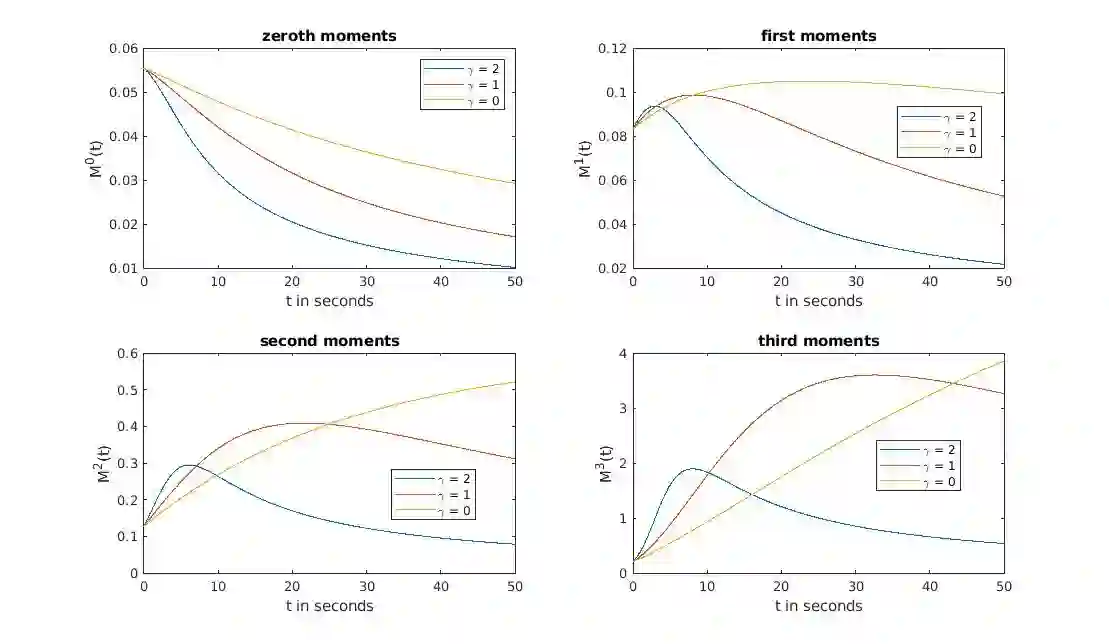
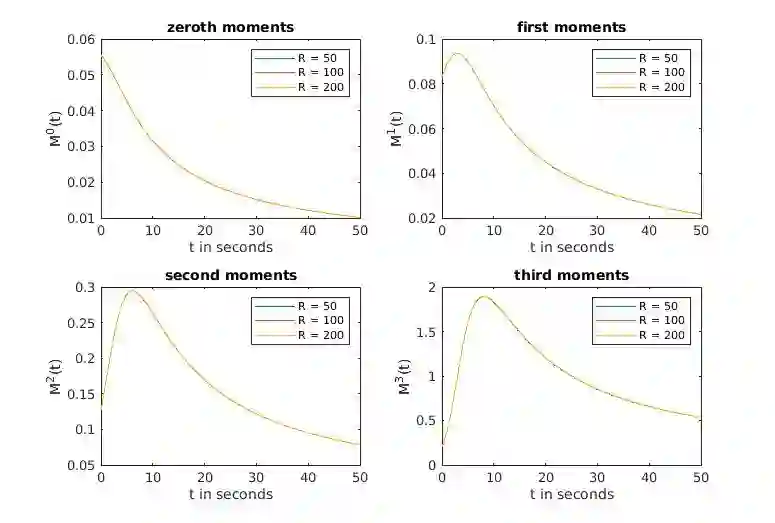
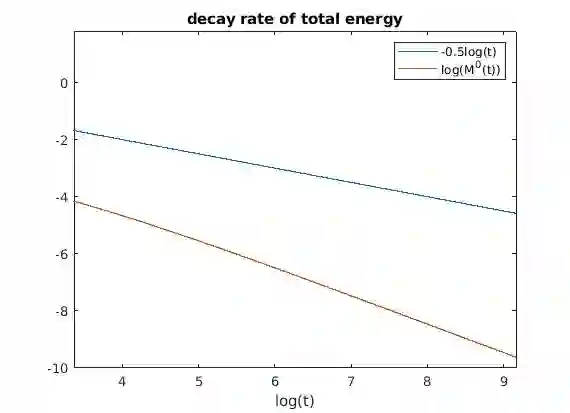
We introduce a finite volume scheme to solve isotropic 3-wave kinetic equations. We test our numerical solution against theoretical results concerning the long time behavior of the energy and observe that our solutions verify the energy cascade phenomenon. Up to our knowledge, this is the first numerical scheme that could capture the long time asymptotic behavior of solutions to isotropic 3-wave kinetic equations, where the energy cascade can be observed. Our numerical energy cascade rates are in good agreement with the theoretical one obtained by Soffer and Tran. Our finite volume algorithm relies on a new identity, that allows one to reduce the number of terms needed to be approximated in the collision operators.
翻译:我们引入一个数量有限的计划来解决异向3波动动方程式问题。 我们根据关于能源长期行为的理论结果测试我们的数字解决方案, 并观察我们的解决方案验证能源级联现象。 据我们所知,这是第一个可以捕捉长期无症状的解决异向3波动动方程式的办法, 在那里可以观察到能源级联。 我们的数字能源级联率与Soffer和Tran获得的理论率相当一致。 我们的有限量算法依赖于一个新的身份, 从而可以减少碰撞操作者需要近似的条件数量。