On the Interpolation Effect of Score Smoothing in Diffusion Models

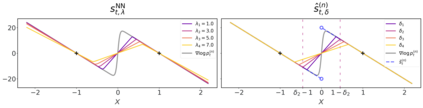
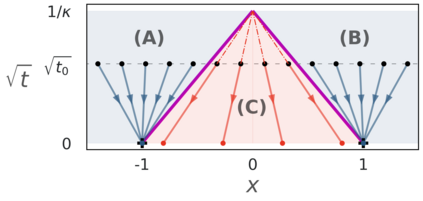
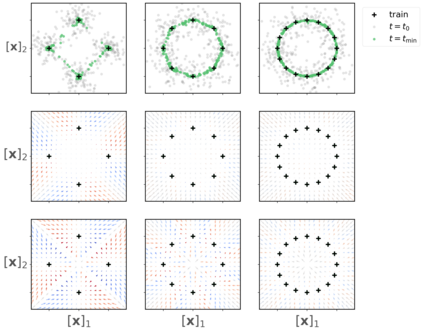
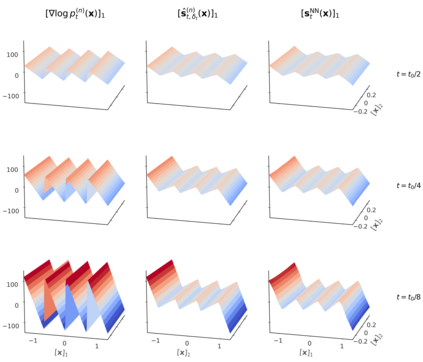
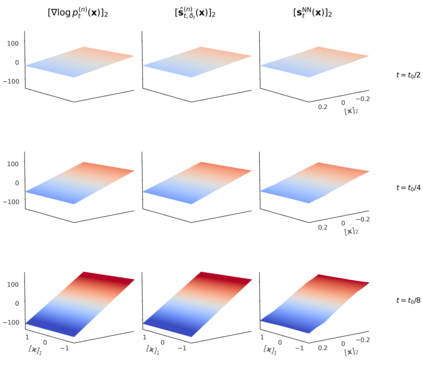
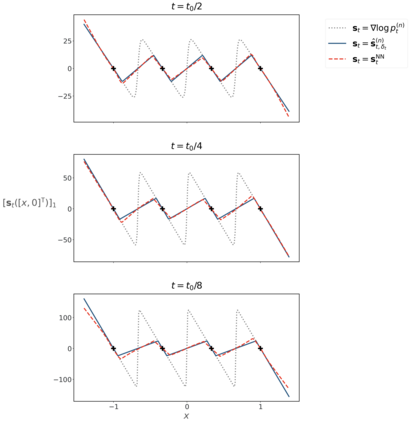
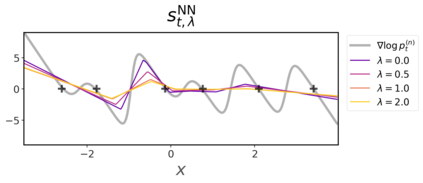
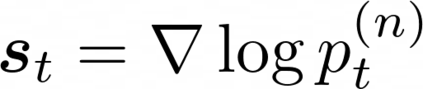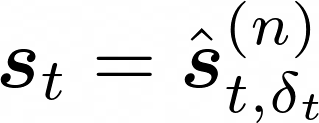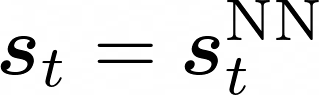Score-based diffusion models have achieved remarkable progress in various domains with the ability to generate new data samples that do not exist in the training set. In this work, we study the hypothesis that such creativity arises from an interpolation effect caused by a smoothing of the empirical score function. Focusing on settings where the training set lies uniformly in a one-dimensional subspace, we show theoretically how regularized two-layer ReLU neural networks tend to learn approximately a smoothed version of the empirical score function, and further probe the interplay between score smoothing and the denoising dynamics with analytical solutions and numerical experiments. In particular, we demonstrate how a smoothed score function can lead to the generation of samples that interpolate the training data along their subspace while avoiding full memorization. Moreover, we present experimental evidence that learning score functions with neural networks indeed induces a score smoothing effect, including in simple nonlinear settings and without explicit regularization.