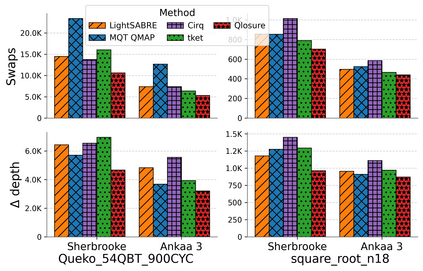
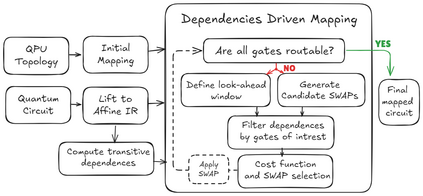
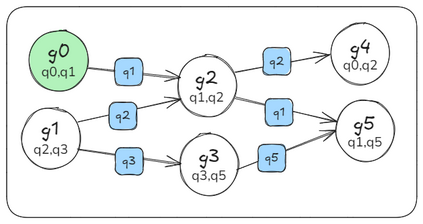
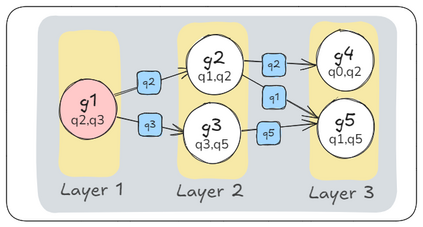
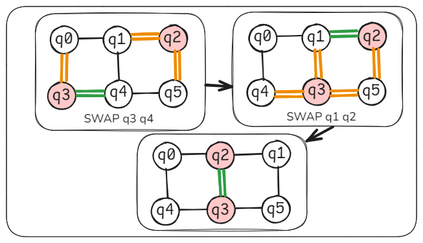
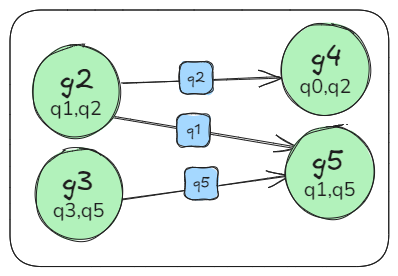
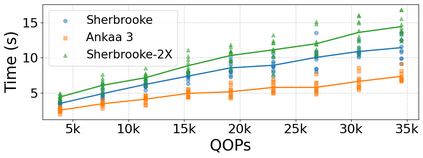
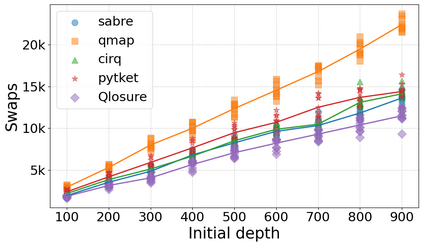
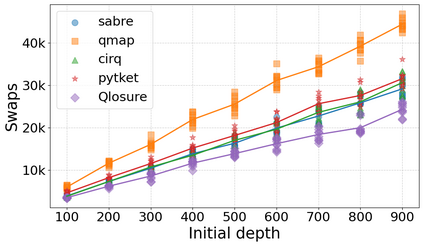
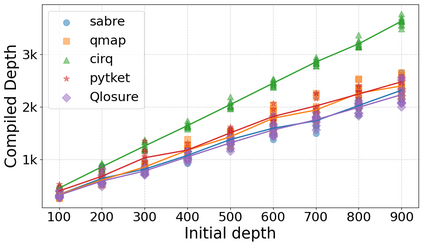
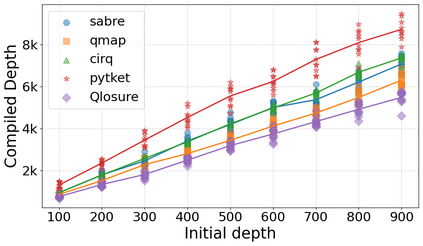
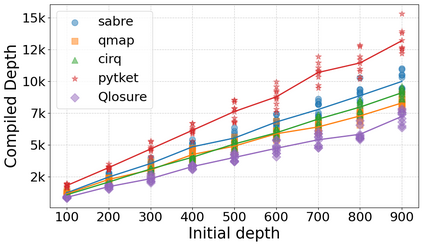
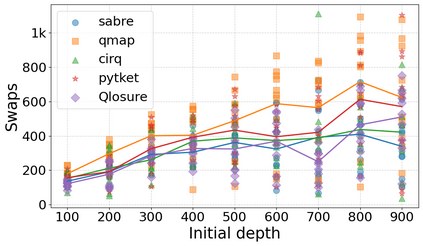
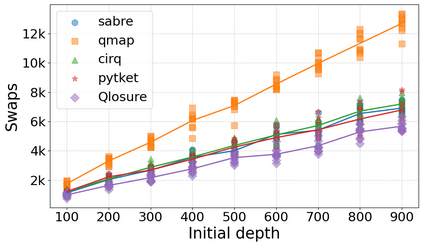
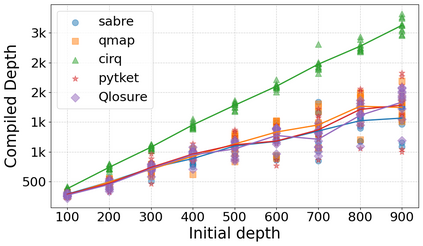
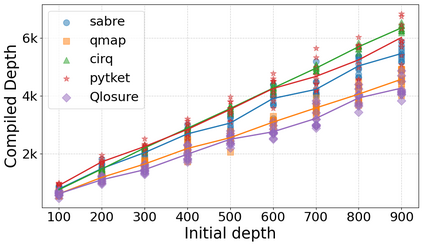
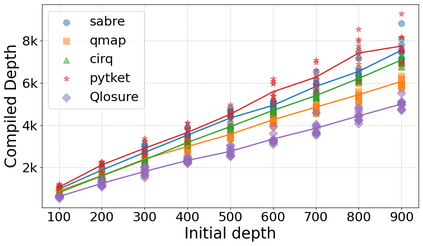
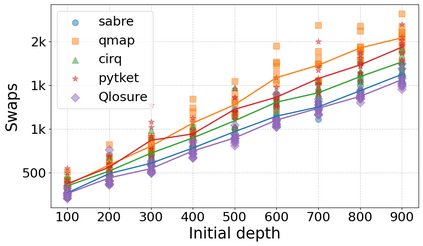
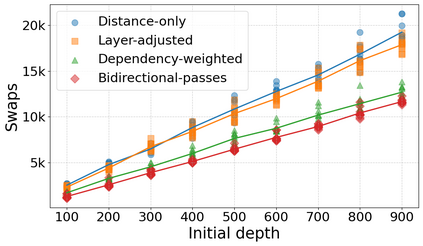
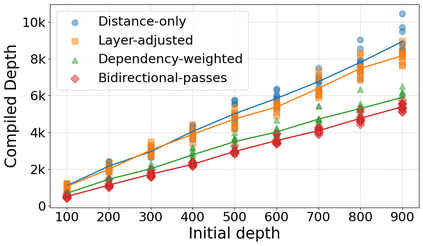
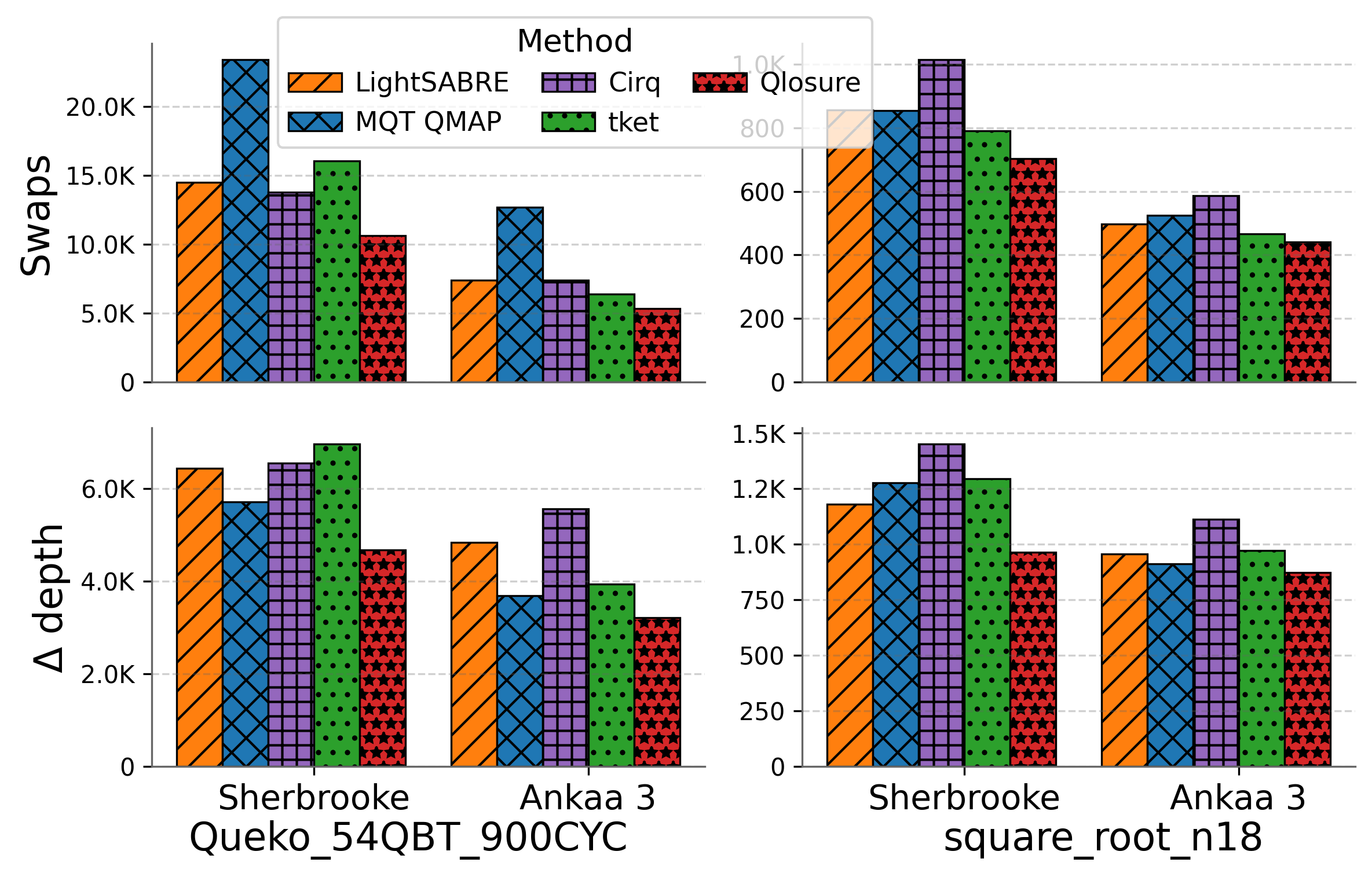
Qubit Mapping is a critical task in Quantum Compilation, as modern Quantum Processing Units (QPUs) are constrained to nearest-neighbor interactions defined by a qubit coupling graph. This compiler pass repairs the connectivity of two-qubit gates whose operands are not adjacent by inserting SWAP gates that move the state of qubits between directly connected qubits. Deciding when to introduce SWAPs while minimizing their count is critical because the error in quantum programs increases exponentially with the circuit latency, measured in number of gates along the critical path of the circuit. Prior work for this problem relied on heuristics and exact methods that partition the circuit into two or more layers, but failed to exploit valuable dependence information in any form. This paper introduces a novel qubit mapping algorithm based on the weight of transitive dependences. The introduced mapper models quantum circuits with affine abstractions thereby yielding the ability to compute transitive dependences. In turn, the newfound information is used to partition circuits by dependence distances and compute, efficiently, distinct weights for each layer. We evaluate the efficiency of our mapper on IBM and Rigetti QPUs, using the large datasets from the QUEKO and QASMBench benchmark suites, and against four baseline tools (QMAP, Sabre, Cirq and TKET), demonstrating notable improvements in circuit depth and swap count while delivering competitive scalability.
翻译:暂无翻译