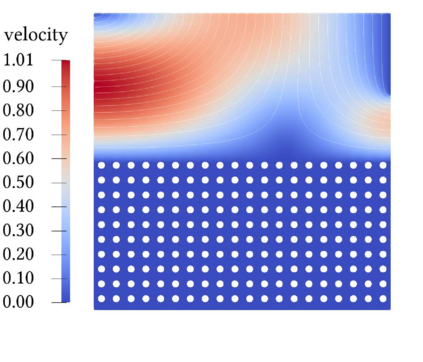
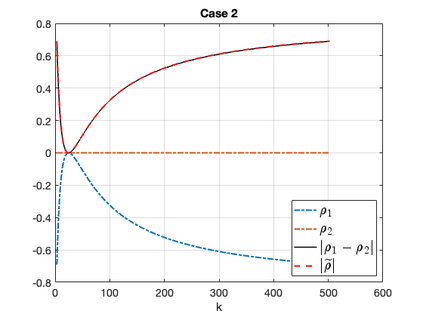
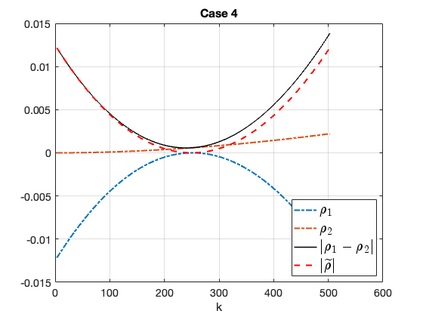
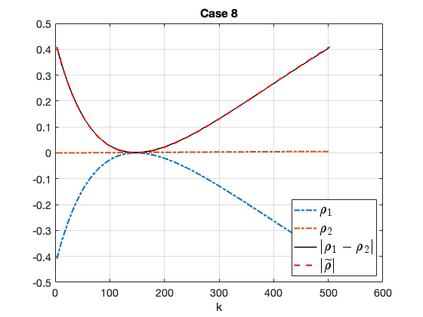
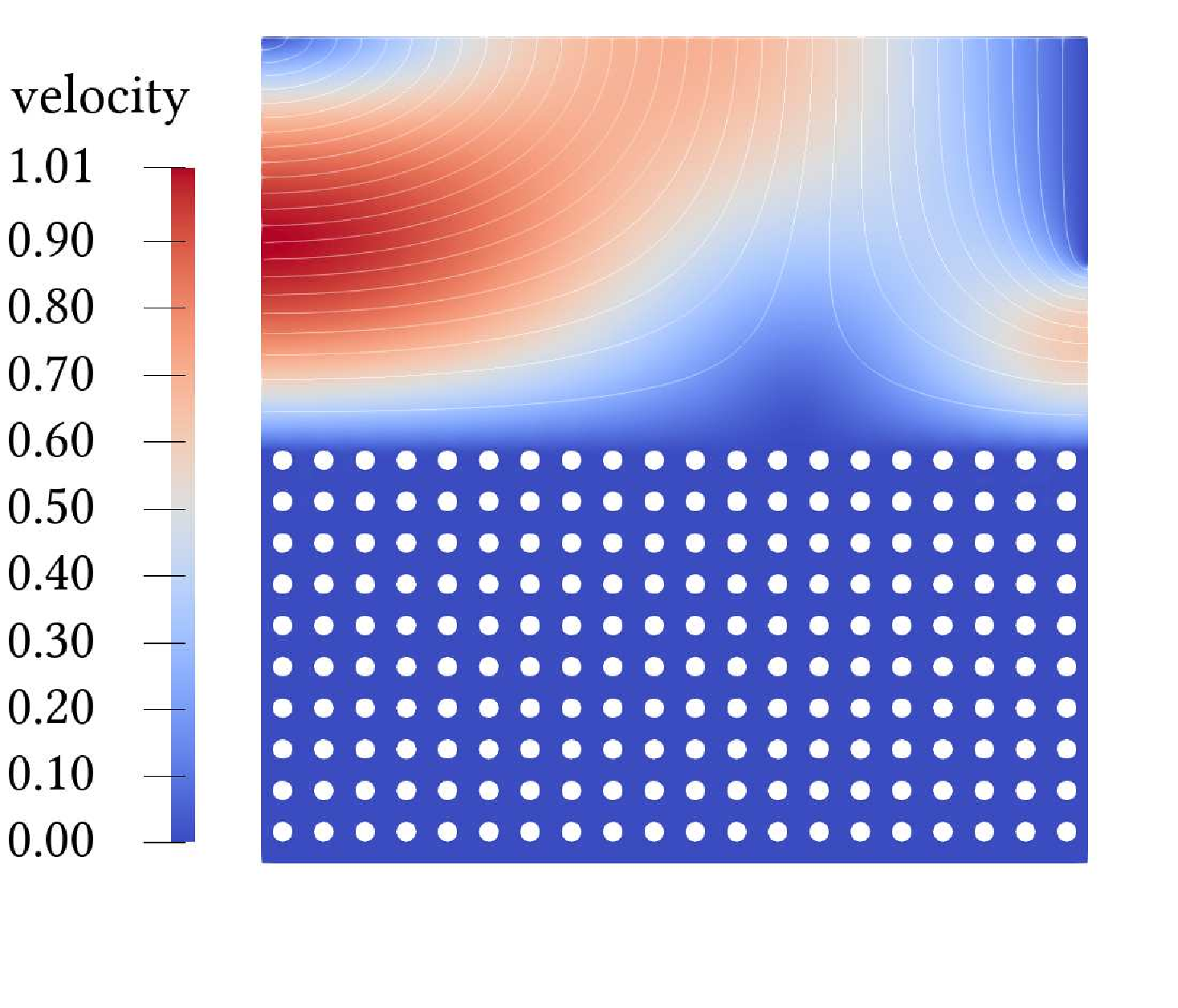
Due to their wide appearance in environmental settings as well as industrial and medical applications, the Stokes-Darcy problems with different sets of interface conditions establish an active research area in the community of mathematical modelers and computational scientists. For numerical simulation of such coupled problems in applications, robust and efficient computational algorithms are needed. In this work, we consider a generalization of the Beavers-Joseph interface condition recently developed using homogenization and boundary layer theory. This extension is applicable not only for the parallel flows to the fluid-porous interface as its predecessor, but also for arbitrary flow directions. To solve the Stokes-Darcy problem with these generalized interface conditions efficiently, we develop and analyze a Robin-Robin domain decomposition method using Fourier analysis to identify optimal weights in the Robin interface conditions. We study efficiency and robustness of the proposed method and provide numerical simulations which confirm the obtained theoretical results.
翻译:暂无翻译