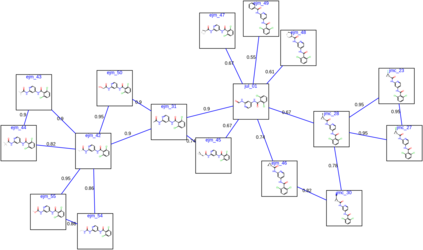
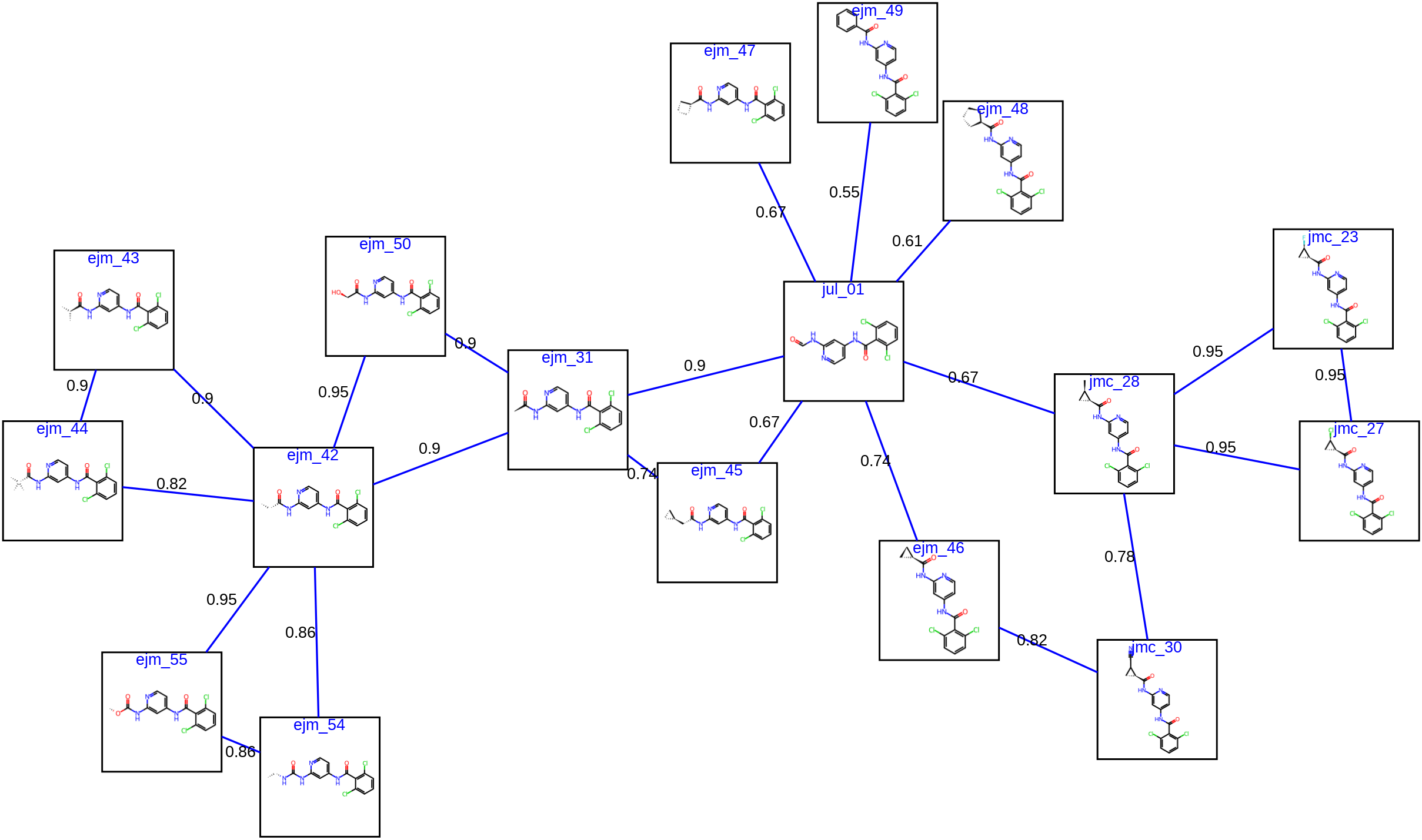
In recent years, free energy perturbation (FEP) calculations have garnered increasing attention as tools to support drug discovery. The lead optimization mapper (Lomap) was proposed as an algorithm to calculate the relative free energy between ligands efficiently. However, Lomap requires checking whether each edge in the FEP graph is removable, which necessitates checking the constraints for all edges. Consequently, conventional Lomap requires significant computation time, at least several hours for cases involving hundreds of compounds, and is impractical for cases with more than tens of thousands of edges. In this study, we aimed to reduce the computational cost of Lomap to enable the construction of FEP graphs for hundreds of compounds. We can reduce the overall number of constraint checks required from an amount dependent on the number of edges to one dependent on the number of nodes by using the chunk check process to check the constraints for as many edges as possible simultaneously. Moreover, the output graph is equivalent to that obtained using conventional Lomap, enabling direct replacement of the original Lomap with our method. With our improvement, the execution was tens to hundreds of times faster than that of the original Lomap. https://github.com/ohuelab/FastLomap
翻译:近年来,自由能扰动(FEP)计算作为支持药物发现的工具引起了越来越多的关注。 铅优化映射器(Lomap)被提出作为一种计算配体之间相对自由能的有效算法。 然而,Lomap需要检查FEP图中的每个边缘是否可移除,这需要检查所有边缘的约束条件。 因此,传统的Lomap需要较长的计算时间,对于涉及数百种化合物的情况至少需要几个小时,并且对于具有数以万计边缘的情况是不切实际的。 在本研究中,我们旨在降低Lomap的计算成本,以便构建数百个化合物的FEP图谱。 我们可以通过使用块检查过程将尽可能多的边缘同时检查约束条件,从而将总体约束检查数量从与边数相关的数量减少到与节点数相关的数量。 此外,输出的图形与传统的Lomap得到的图形相当,可以直接替换原始的Lomap使用我们的方法。 利用本研究的改进,执行速度比原始的Lomap快几十到几百倍。 https://github.com/ohuelab/FastLomap