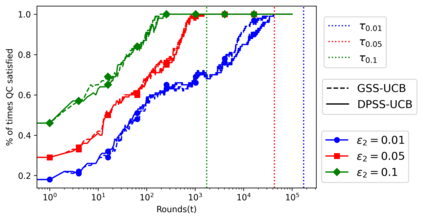
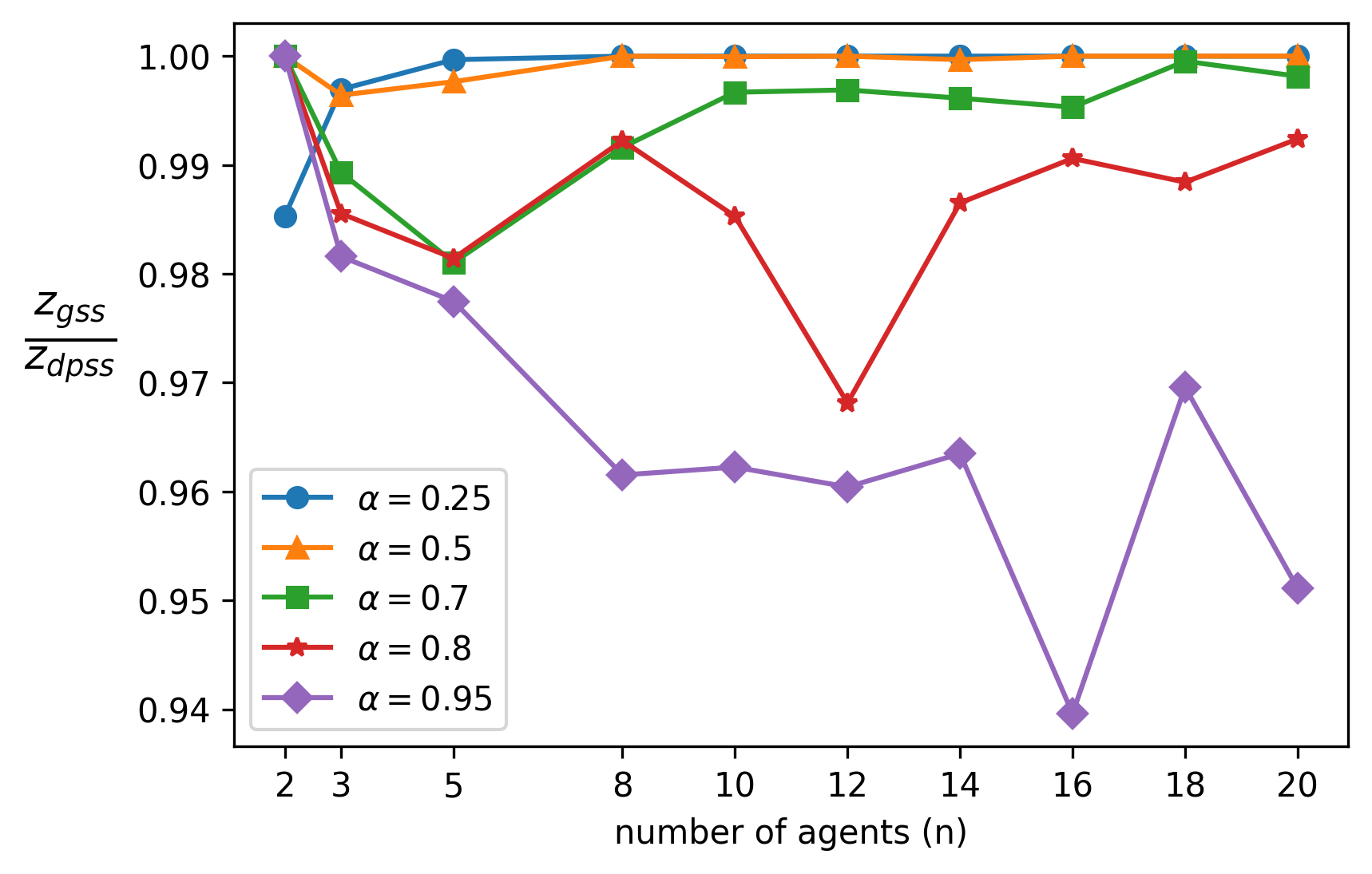
We explore the class of problems where a central planner needs to select a subset of agents, each with different quality and cost. The planner wants to maximize its utility while ensuring that the average quality of the selected agents is above a certain threshold. When the agents' quality is known, we formulate our problem as an integer linear program (ILP) and propose a deterministic algorithm, namely \dpss\ that provides an exact solution to our ILP. We then consider the setting when the qualities of the agents are unknown. We model this as a Multi-Arm Bandit (MAB) problem and propose \newalgo\ to learn the qualities over multiple rounds. We show that after a certain number of rounds, $\tau$, \newalgo\ outputs a subset of agents that satisfy the average quality constraint with a high probability. Next, we provide bounds on $\tau$ and prove that after $\tau$ rounds, the algorithm incurs a regret of $O(\ln T)$, where $T$ is the total number of rounds. We further illustrate the efficacy of \newalgo\ through simulations. To overcome the computational limitations of \dpss, we propose a polynomial-time greedy algorithm, namely \greedy, that provides an approximate solution to our ILP. We also compare the performance of \dpss\ and \greedy\ through experiments.
翻译:我们探讨中央规划员需要选择一组代理人,每个代理人质量和成本不同。 计划员希望最大限度地扩大其效用, 同时确保所选代理人的平均质量超过某一阈值。 当知道代理人的质量时, 我们将问题发展成一个整数线性程序( ILP), 并提议一个确定性算法, 即\ dps\ 提供我们 ILP 的确切解决方案。 然后当代理员的品质未知时, 我们再考虑它的设置。 我们把它模拟为多Arm Bandit (MAB) 问题, 并提议\ newalgo\ 来学习多轮的品质。 我们进一步展示了在某轮后, $tau,\ tau,\ nnewalgo\ 输出出一组能满足平均质量限制的代理人。 下一步我们提供$tau, 并证明在美元回合后, 算出我们通过美元=P$( $) 和美元( t$) 的比较结果, 并提议在多轮数中学习质量 。 我们进一步说明在数回合中, 也就是Nevalgo\\\\ imalalalal 的计算结果, imalalationalalalalal dalbalbalbalbalation 的效能的效能, y ex ex ex ex ex exalationalations expalations a calations a cald ex ex exbalations ex ex expalations expalation ex ex extracumentalmentalations ex ex。