Probabilistic Robust Autoencoders for Anomaly Detection

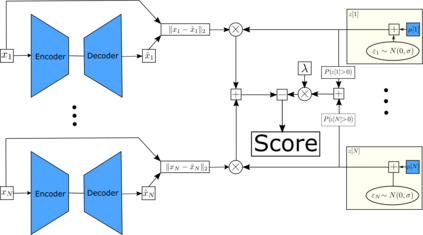
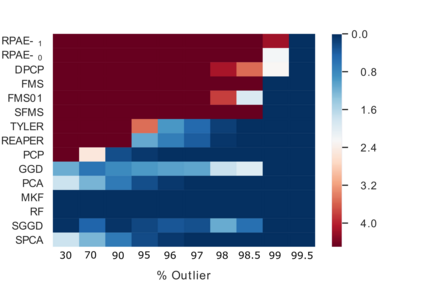
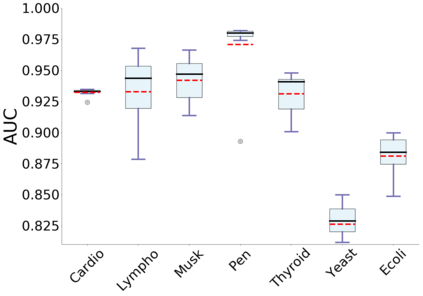
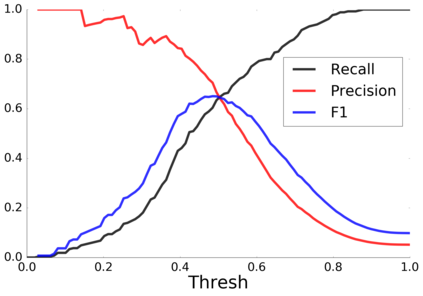
Empirical observations often consist of anomalies (or outliers) that contaminate the data. Accurate identification of anomalous samples is crucial for the success of downstream data analysis tasks. To automatically identify anomalies, we propose a new type of autoencoder (AE) which we term Probabilistic Robust autoencoder (PRAE). PRAE is designed to simultaneously remove outliers and identify a low-dimensional representation for the inlier samples. We first describe Robust AE (RAE) as a model that aims to split the data to inlier samples from which a low dimensional representation is learned via an AE, and anomalous (outlier) samples that are excluded as they do not fit the low dimensional representation. Robust AE minimizes the reconstruction of the AE while attempting to incorporate as many observations as possible. This could be realized by subtracting from the reconstruction term an $\ell_0$ norm counting the number of selected observations. Since the $\ell_0$ norm is not differentiable, we propose two probabilistic relaxations for the RAE approach and demonstrate that they can effectively identify anomalies. We prove that the solution to PRAE is equivalent to the solution of RAE and demonstrate using extensive simulations that PRAE is at par with state-of-the-art methods for anomaly detection.